Mesh generation#
Loading a mesh file#
XLiFE++ allows you to read various mesh file formats. Let’s start with some examples:
//! gmsh file reader
Mesh m("square.msh", _name="Square Mesh");
//! medit file reader using key _format
Mesh m("square", _name="Square Mesh", _format=medit);
The first argument is always the file name, with or without extension. Next come one or several parameters set by a key-value system:
_name: to define the mesh name.
_format: to define the mesh format. If the filename contains a legacy file extension, it will be prior to the key _format
See also
There is an advanced key, _dim, restraining the dimension of mesh nodes. Default is 0 for automatic behavior. Normally, you should not have to use this argument.
Mesh m1("mesh.vtk", _name="My Mesh M1"); // loading a VTK mesh file
Mesh m2("mesh.vtu", _name="My Mesh M2"); // loading a VTU mesh file
Mesh m3("mesh.msh", _name="My Mesh M3"); // loading a GMSH mesh file
Mesh m4("mesh.geo", _name="My Mesh M4"); // loading a GMSH script file
Mesh m5("mesh.mel", _name="My Mesh M5"); // loading a MELINA mesh file
Mesh m6("mesh.ply", _name="My Mesh M6"); // loading a PLY mesh file
which create six Mesh objects called m1, m2, m3, m4, m5 and m6.
To have more information about the VTK and VTU file formats, please go to Paraview website.
The MELINA file format is the input format of the Melina finite element library, ancestor of XLiFE++.
To have more information on the PLY file format, please go to Polygon File Format.
To have more information about GMSH, please go to Gmsh website. You will have everything you need about the msh format and about the geo scripts.
Important
If you load a geo file, XLiFE++ will call Gmsh to create the corresponding msh file, which is then read. Consequently, Gmsh needs to be installed on your computer and the executable file, called gmsh, should be found through your PATH environment variable. If Gmsh is installed after XLiFE++, XLiFE++ needs to be reinstalled.
Generating a mesh from a geometry#
XLiFE++ owns some constructors that allow to create meshes based on canonical geometries (inherited classes of the Geometry class) :
2D :
Polygon,Triangle,Quadrangle,Parallelogram,Rectangle,SquareGeo,Ellipse,Disk,ParametrizedSurface,SplineSurface3D :
Polyhedron,Tetrahedron,Hexahedron,Parallepiped,Cuboid,Cube,Ellipsoid,Ball,Trunk,Cylinder,Prism,Cone,Pyramid,RevTrunk,RevCylinder,RevCone.
By using + or - operators, canonical geometries can be merged or holes created when configuration is not too intricate. See Geometry definition for a detailed description of canonical geometries and how to use operators.
Let’s start with some examples:
// P1 structured mesh of segment [0,1] with 10 nodes.
Mesh m1D(Segment(_xmin=0., _xmax=1., _nnodes=10, _domain_name="Omega"),
_generator=structured);
// P1 unstructured mesh of disk ((0,0,1),2.5) with 40 nodes.
Disk D(_center=Point(0.,0.,1.), _radius=2.5, _nnodes=40, _domain_name="Omega",
_side_names="Gamma");
Mesh m2D(D, _shape=triangle, _generator=subdiv); // using subdivision generator
// Q2 unstructured mesh of cuboid [0,2]x[0,1]x[0,4] with 20, 10, 40 nodes on edges
Cuboid C(_v1={0.,0.,0.}, _v2={2.,0.,0.}, _v4={0.,1.,0.}, _v5={0.,0.,4.},
_nnodes={20,10,40}, _domain_name="Omega")
Mesh m3D(C, _shape=hexahedron, _order=2, _generator=gmsh); // using gmsh generator
A Mesh can be defined from any geometrical object to be meshed (such as Segment, Quadrangle, Hexahedron, …). Geometry definition carries information about the mesh step (keys _nnodes or _hsteps) and the domain names (keys _domain_name and _side_names). See Geometry definition.
There are optional arguments with a key-value system:
_shape: to define the shape of the mesh cell (segment, triangle, quadrangle, tetrahedron, hexahedron, prism or pyramid). The default value is the simplex cell related to the dimension of the geometry: segment for 1D geometries, triangle for 2D geometries and tetrahedron for 3D geometries
_generator: to define the way the mesh is generated:
structured: a structured mesh can be built for canonical geometries only (Segment,Parallelogram,Rectangle,SquareGeo,Parallelepiped,CuboidandCube); the order of the mesh is necessarily one. See Structured generator (internal) for more details.subdiv: an unstructured mesh can be built using the so-called subdivision generator for the following geometries:Cube,Ball,RevTrunk,RevCone,RevCylinder,DiskandSetOfElems. The order can be any integer \(k>0\). See Unstructured subdivision generator (internal) for more details.gmsh: for more complicated geometries, with a nested call of the Gmsh software; the order depends on the chosen shape (refer to Gmsh documentation). See Gmsh generator for more details.gmshOC: for more complicated geometries involving non trivial intersection or union of geometries, with a nested call of the Gmsh software using the OpenCASCADE factory. See Open Cascade extension for more details.fromParameterization: to define a mesh of a parametrized geometry from the mesh of the parameters’ support (see Mesh from parametrization).
_order: to define the interpolation order of the mesh elements; possible values depend on the mesh generator. Default is 1.
_name: to define the mesh name
Important
If you want to mesh a 2D geometry with segment elements, only borders will be meshed. The same goes for 3D geometries mesh with triangles or quadrangles.
Structured generator (internal)#
When the structured generator is chosen (_generator=structured), one can create a mesh of order 1:
of a segment,
of a triangle with triangles,
of a parallelogram with triangles or quadrangles,
of a parallelepiped with hexahedra, prisms or pyramids.
The following boundary geometries are also handled:
the boundary of the triangle meshed by segments,
the boundary of the parallelogram meshed by segments,
the boundary of the parallelepiped meshed by triangles or quadrangles
One has to declare an object of type Geometry, more precisely of one of its derived type managed by the structured generator.
Example 1:
Mesh mesh1dP1(Segment(_xmin=0, _xmax=1, _nnodes=11), _generator=structured, _name="P1 mesh of [0,1], step=0.1");
This builds a mesh of the interval \([0,1]\) with 10 subintervals. The 1D domain will be called “Omega”.
Example 2:
Strings sn(4);
sn[0] = "Gamma_bottom"; sn[2] = "Gamma_top";
Mesh mesh2dP1(Rectangle(_xmin=0, _xmax=1, _ymin=1, _ymax=3, _nnodes=Numbers(3, 5), _side_names=sn), _generator=structured, _name="P1 mesh of [0,1]x[1,3]");
This builds a mesh of the rectangle \([0,1]\times[1,3]\) with triangles. The interval \([0,1]\) is subdivided into 2 subintervals; the interval \([1,3]\) is subdivided into 4 subintervals. Only the plain domain “Omega” and the two side domains “Gamma_bottom” and “Gamma_top” will be created. Left and right side domains will not be created as they have no names.
Some options may be used to control the splitting of elementary rectangle into triangles. This is controlled by the key _split_pattern:
Rectangle R(_xmin=0, _xmax=1, _ymin=1, _ymax=3, _nnodes=Numbers(6, 10));
Mesh mesh2dP1l(R, _generator=structured); // default is left splitting
Mesh mesh2dP1r(R, _generator=structured, _split_pattern=right);
Mesh mesh2dP1a(R, _generator=structured, _split_pattern=alternate);
Mesh mesh2dP1c(R, _generator=structured, _split_pattern=cross);
Mesh mesh2dP1rand(R, _generator=structured, _split_pattern=random);
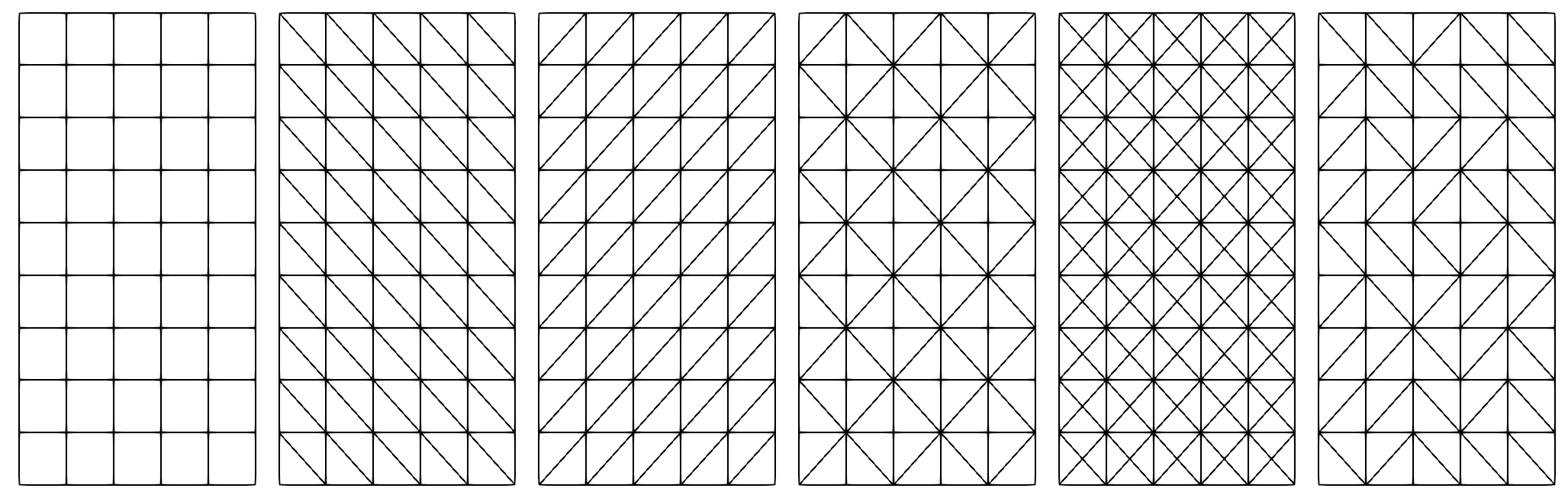
Fig. 41 Mesh of a rectangle with respectively left, right, alternate, cross and random splitting#
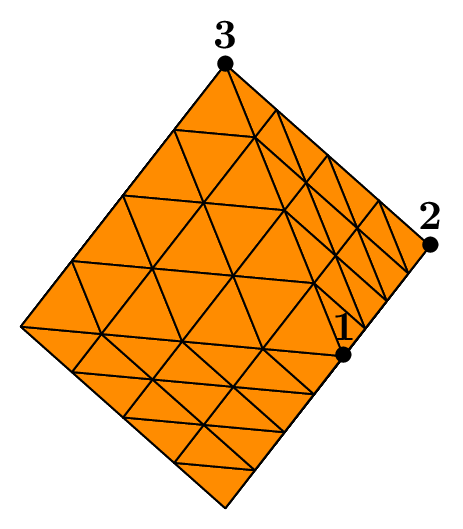
Example 3:
Strings sn={"Gamma1","Gamma2","Gamma3"};
Triangle tri(_v1=Point{2.,0.},_v2=Point{0.,0.},_v3=Point{5.,1.},_nnodes={9,27,27},
_domain_name="T",_side_names=sn);
Mesh mesh2dP1t(tri,_shape=_triangle,_generator=_structured);
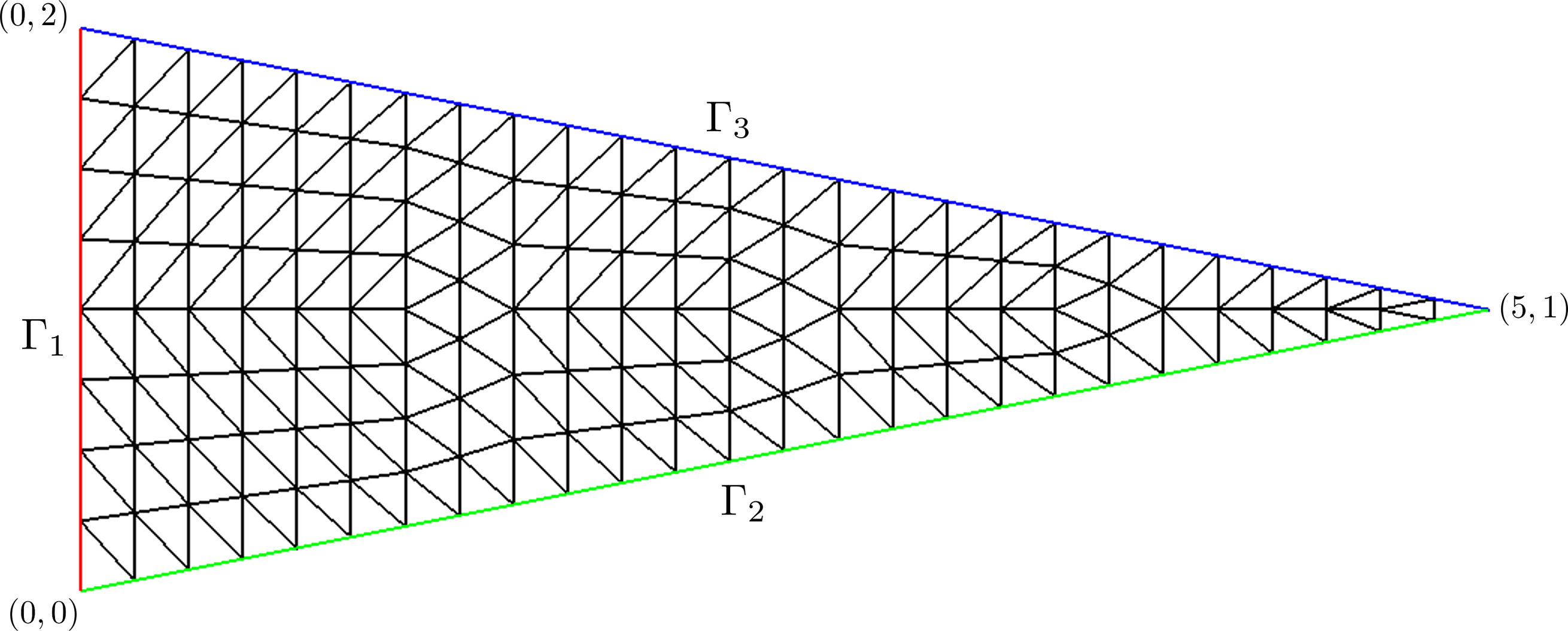
Fig. 42 P1 mesh of a triangle with 9 nodes on base and 27 nodes on sides#
Note
The structured generator for triangles requires the same number of nodes on both sides (say p) and the number of nodes on base (say q) must satisfy the relation \(p\ge q \ge 3\).
Example 4:
Strings sn("z=1", "z=5", "y=1", "y=3", "x=0", "x=1");
Mesh mesh3dQ1(Cuboid(_xmin=0, _xmax=1, _ymin=1, _ymax=3, _zmin=1, _zmax=5, _nnodes=Numbers(3, 5, 9), _side_names=sn), _shape=hexahedron, _generator=structured, _name="Q1 mesh of [0,1]x[1,3]x[1,5]");
This builds a mesh of the parallelepiped \([0,1]\times[1,3]\times[1,5]\) with hexahedra. The interval \([0,1]\) is subdivided into 2 subintervals; the interval \([1,3]\) is subdivided into 4 subintervals; the interval \([1,5]\) is subdivided into 8 subintervals. The plain domain “Omega” and the 6 boundary domains will be created with their corresponding names.
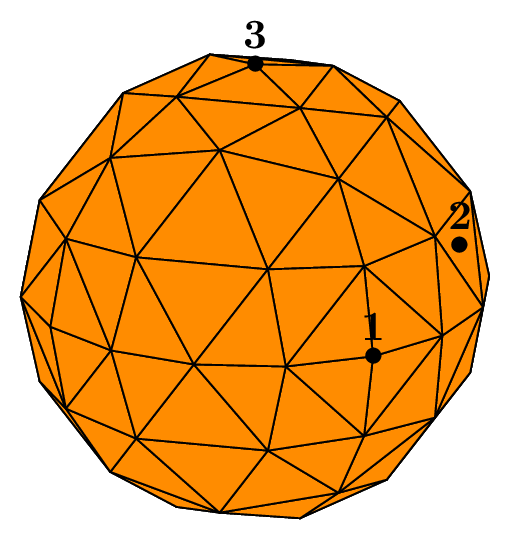
Unstructured subdivision generator (internal)#
When the subdivision generator is chosen (_generator=subdiv), one can create a mesh of any order based on the following volumetric geometries:
The sphere meshed by tetrahedra,
the cube meshed by tetrahedra or hexahedra,
the cone or truncated cone, which may be a cylinder, meshed by tetrahedra or hexahedra.
The following surfacic geometries are also handled:
The boundary of the sphere meshed by triangles,
the boundary of the cube meshed by quadrangles,
the boundary of the cone or truncated cone meshed by triangles or quadrangles,
the disk meshed by triangles or quadrangles,
mesh built from an initial set of triangles or quadrangles in 2D or 3D.
The generator consists in starting from an initial mesh, a kind of “seed” mesh, namely a set of elements, and builds the mesh by subdividing each of them by cutting each edge in the middle until a prescribed so-called “subdivision depth” is reached. A subdivision depth equal to 0 gives a mesh reduced to the initial mesh. A triangle and a quadrangle are subdivided into 4 pieces; a tetrahedron and a hexahedron is subdivided into 8 pieces. Thus, at each subdivision, the number of elements of the mesh is multiplied by 4 for a surface mesh, by 8 for a volumetric one, and the characteristic dimension of the elements is halved.
One has to declare an object of type Geometry, more precisely of one of its derived type managed by the subdivision generator.
Example 1:
Number order = 1, nbpts=5;
Ball sph1(_center=Point(0.,0.,0.), _radius=1., _nnodes=5, _type=1);
Mesh m1(sph1, _order=1, _generator=subdiv);
Ball sph2(_center=Point(0.,0.,0.), _radius=1., _nnodes=5, _nboctants=8, _type=1);
Mesh m2(sph2, _order=1, _generator=subdiv);
Ball sph3(_center=Point(0.,0.,0.), _radius=1., _nnodes=5, _type=0);
Mesh m3(sph3, _order=1, _generator=subdiv);
Ball sph4(_center=Point(0.,0.,0.), _radius=1., _nnodes=5, _nboctants=8, _type=0);
Mesh m4(sph4, _order=1, _generator=subdiv);
This build a mesh of the sphere by refining a seed mesh and by projecting the generated points on the sphere (_type=1)or not (_type=0). The seed mesh consists of small mesh in each octant of the cartesian axes. Defining how many octants will be generated is controlled by the key _nboctants. For the Ball, the default value is not 8 for the whole sphere, but 0. In this case,
The following figure shows this in the case of a subdivision depth equal to 2. Each figure corresponds to the result of the following code, using the unit sphere and _type varying from 0 to 1:
Fig. 43 Volumic meshes of the ball according _type and _nboctants (0 or 8)#
Example 2:
RevCylinder cyl2e(_center1=Point(0.,0.,0.), _center2=Point(0.,0.,1.), _radius=1., _end1_shape=gesEllipsoid, _end1_distance=0.5, _end2_shape=gesCone, _end2_distance=1., _nnodes=5);
Mesh P1VolMeshTetCylE(cyl2e, _generator=subdiv);
This build a mesh of a revolution cylinder whose revolution axis is \(e_z\) and with unit disk as basis. This cylinder is covered by 2 hats: a half-ellipsoid on the first basis and a cone on the second basis. The following figure shows such a configuration.

Fig. 44 Volumic meshes of a “pen”: a truncated cone with ellipsoidal and conical hats#
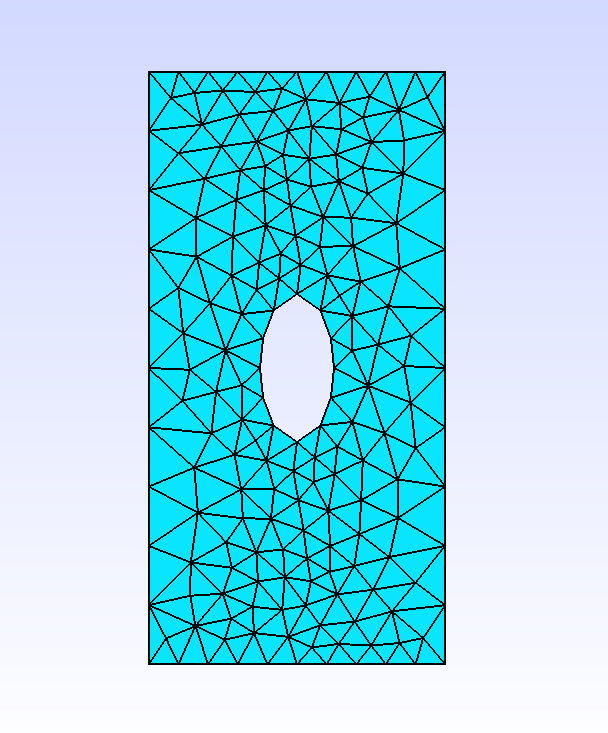
Example 3:
...
SetOfElems sot(tpts, telems, tbounds, triangle, 3);
Mesh mT(sot, _generator=subdiv);
SetOfElems soq(qpts, qelems, qbounds, quadrangle, 3);
Mesh mQ(soq, _shape=quadrangle, _generator=subdiv);
This build 2 meshes from an elementary set of triangles or quadrangles (SetOfElems) with 3 refinement depths.
The following figure shows two examples, in 3D with triangles, in 2D with quadrangles on a domain with a hole.
Fig. 45 Meshes from initial set of triangles and quadrangles#
The mesh of triangle is based on an initial set of 2 triangles \(\{1,2,3\}\) and \(\{1,4,2\}\), stored in the vector elems. The 4 points are Point(0.,0.,0.), Point(1.,0.,0.), Point(0.,1.,0.3), Point(0.,-1.,0.3)
stored in the vector tpts. Four boundaries are defined.
A boundary is simply defined by the list of point numbers lying on it, in any order. Thus, here, the four boundaries are \(\{1,4\}, \{4,2\}, \{2,3\}\) and \(\{1,3\}\);
they are stored in the vector tbounds. The same apply for the set of quadrangles.
Gmsh generator#
Using the Gmsh interface to define meshes allows you to define more canonical geometries than both previous generators:
Segments, ellipses, circles, elliptical or circular arcs as 1D geometries;
Quadrangles, rectangles, squares, disks, elliptical surfaces, spheres, ellipsoids, triangles as 2D geometries with either triangular or quadrangular mesh elements;
Hexahedra, parallelepipeds, cubes, balls, tetrahedra, cylinders, prisms, pyramids as 3D geometries with either tetrahedral or hexahedral mesh elements.
When you use it, 2 files will be generated in your working directory:
xlifepp_script.geo-
This is the input file of Gmsh. To simplify its writing, XLiFE++ provides a macro file included in this one. If you look at this file, you will find a very elegant way to define meshes with Gmsh.
xlifepp_script.msh-
This is the real mesh file, generated by a system call to Gmsh from the .geo file. This file is loaded by XLiFE++.
Next to this, you can define 2 types of complicated geometries : the so-called “composite” and “loop” geometries.
Please see Combining geometries for definition of composite geometries and the use of operators + and -, and see Definition of a geometry from its boundary for definition of loop geometries and the use of surfaceFrom and volumeFrom routines.
Example 1:
Rectangle r(_xmin=-3, _xmax=3, _ymin=-2, _ymax=2, _nnodes=Numbers(33,22), _domain_name="Omega_ext");
Ellipse e(_center=Point(0,0), _xlength=1, _ylength=0.5, _nnodes=11, _domain_name="Omega_int");
Mesh m1(r-e, _generator=gmsh);
Mesh m2(r+e, _generator=gmsh);
This generates for m1 a triangular mesh with only one surfacic domain “Omega_ext”. For m2, this generates a triangular mesh of the rectangle with 3 surfacic domains:
“Omega_ext” will be the domain of the difference between the rectangle and the ellipse (the same as in
m1)“Omega_int” will be the domain inside the ellipse
“Omega” will be the union of “Omega_ext” and “Omega_int”
Fig. 46 Gmsh view of m1 and m2. Domain “Omega_ext” is in cyan, domain “Omega_int” is in yellow.#
Example 2:
Point a(-1.5,-4.), b(1.5,-4.), c(2.,-3.5), d(2.,3.5);
Point e(1.5,4.), f(-1.5,4.), g(-2.,3.5), h(-2.,-3.5);
Segment s1(_v1=a, _v2=b, _nnodes=21, _domain_name="AB");
CircArc c1(_center=Point(3.5,0.5), _v1=b, _v2=c, _nnodes=5, _domain_name="BC");
Segment s2(_v1=c, _v2=d, _nnodes=11, _domain_name="CD");
CircArc c2(_center=Point(3.5,1.5), _v1=d, _v2=e, _nnodes=5, _domain_name="DE");
Segment s3(_v1=e, _v2=f, _nnodes=21, _domain_name="EF");
CircArc c3(_center=Point(0.5,1.5), _v1=f, _v2=g, _nnodes=5, _domain_name="FG");
Segment s4(_v1=g, _v2=h, _nnodes=11, _domain_name="GH");
CircArc c4(_center=Point(0.5,0.5), _v1=h, _v2=a, _nnodes=5, _domain_name="HA");
Mesh mesh2dP1Loop(surfaceFrom(s1+c1+s2+c2+s3+c3+s4+c4), _generator=gmsh);
This generates a triangular mesh of a rounded rectangle defined from its boundaries. Eachh component of the boundary will be a domain: “AB”, “BC”, “CD”, “dE”, “EF, “FG”, “GH”, and “HA”. There will be also a surfacic mesh names “Omega”.
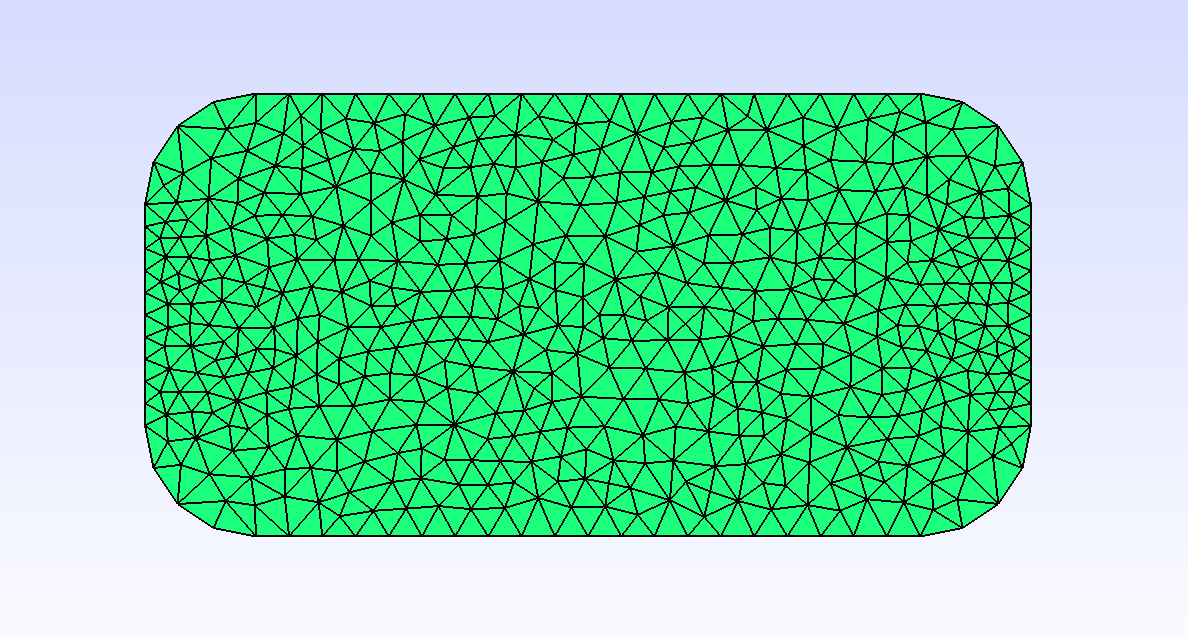
Fig. 47 Gmsh view of a rounded rectangle#
Example 3:
Ellipse e1(_center=Point(0.,0.), _v1=Point(4,0.), _v2=Point(0.,5.), _nnodes=12, _domain_name="Omega1");
Point a(-1.5,-4.); Point b(1.5,-4.); Point c(2.,-3.5); Point d(2.,3.5);
Point e(1.5,4.); Point f(-1.5,4.); Point g(-2.,3.5); Point h(-2.,-3.5);
Segment s1(_v1=a, _v2=b, _nnodes=21, _domain_name="AB");
CircArc c1(_center=Point(3.5,0.5), _v1=b, _v2=c, _nnodes=5, _domain_name="BC");
Segment s2(_v1=c, _v2=d, _nnodes=11, _domain_name="CD");
CircArc c2(_center=Point(3.5,1.5), _v1=d, _v2=e, _nnodes=5, _domain_name="DE");
Segment s3(_v1=e, _v2=f, _nnodes=21, _domain_name="EF");
CircArc c3(_center=Point(0.5,1.5), _v1=f, _v2=g, _nnodes=5, _domain_name="FG");
Segment s4(_v1=g, _v2=h, _nnodes=11, _domain_name="GH");
CircArc c4(_center=Point(0.5,0.5), _v1=h, _v2=a, _nnodes=5, _domain_name="HA");
Geometry sf1=surfaceFrom(s1+c1+s2+c2+s3+c3+s4+c4,"Omega2");
Ellipse e2(_center=Point(1.,2.), _v1=Point(1.5,2.), _v2=Point(1.,3.), _nnodes=12, _domain_name="Omega3");
Ellipse e3(_center=Point(0.,0.), _v1=Point(0.5,0.), _v2=Point(0.,1.), _nnodes=12, _domain_name="Omega4");
Rectangle r2(_xmin=5., _xmax=6., _ymin=0., _ymax=1., _nnodes=6, _domain_name="Omega5");
Segment s5(_v1=Point(5.3,0.5), _v2=Point(5.7,0.5), _nnodes=5);
CircArc c5(_center=Point(5.5,0.5), _v1=Point(5.7,0.5), _v2=Point (5.5,0.7), _nnodes=5);
CircArc c6(_center=Point(5.5,0.5), _v1=Point (5.5,0.7), _v2=Point(5.3,0.5), _nnodes=5);
Geometry sf2=surfaceFrom(s5+c5+c6,"Omega6");
Mesh mesh2dP1Composite3(e1+(sf1+(+(e2+e3))+r2+sf2, _generator=gmsh);
This generates a complex composite geometry whose some components are loop geometries. In most cases, XLiFE++ is able to detect properly if a Geometry is inside another one or not. When it is not possible (and XLiFE++ warns you), you have the possibility to force inclusion by using the unary + operator. This is what is done to tell that the composite geometry e2+e3 is inside sf1.
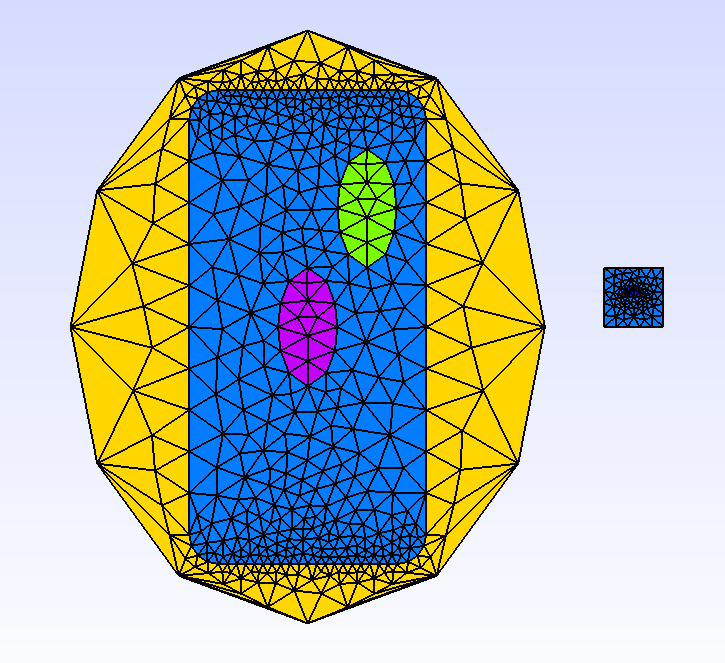
Fig. 48 gmsh view of mesh2dP1Composite3#
Example 4:
Mesh m(Rectangle(_xmin=0., _xmax=2., _ymin=0., _ymax=4., _nnodes=11, _side_names=Strings("Gamma_1", "Gamma_2", "Gamma_3", "Gamma_4")), _generator=gmsh, _pattern=structured);
The gmsh generator also allows generating structured meshes, next to the internal structured generator. To say so, you have an additional key, _pattern, whose default value is unstructured, but which can be used with structured.
Note
By default, Gmsh produces meshes made of first order elements. By using the additional key _order, meshes with element of order from 1 to 5 can be generated; XLiFE++ being able to deal with.
Note
Gmsh is able to deal with cracks. To take advantage of this, XLiFE++ handles cracks in Geometry objects; see Cracking geometries for details.
Open Cascade extension#
Open Cascade Technology (OCT) [1] is a third party open source library dedicated to 3D CAD data. It is a powerful library dealing with canonical geometries but providing complex geometrical operations (union, intersection, difference of geometries, fillet, chamfer, …). The standard geometry engine of XLiFE++ provides only union or difference in the case of one geometry included in another one (if detection is easy). So to go further, XLiFE++ provides an interface to OCT. Obviously, OCT must be installed and activated in XLiFE++ (cmake option).
Footnotes
Warning
OCT interface is still experimental. Use it with caution!
When OCT is enabled, it runs only if the user invokes an explicit OCT function. OCT objects (OCData class) are embedded in XLiFE++ geometry objects but are not allocated by default.
If an OCT function is invoked, OCT object will be allocated on the fly.
The main interest of OCT interface is to mesh complex object, for instance the intersection of two spheres perforated by a cylinder:
Sphere S1(_center=Point(1.,0,0.), _radius=1, _hsteps=0.02, _domain_name="S", _side_names="Sigma");
Sphere S2=translate(S1, _direction={1.5,0.,0.}); // _side_names "Sigma_2"
RevCylinder C(_center1=Point(1,0.,0), _center2=Point(2.5,0.,0.), _radius=0.3, _hsteps=0.02, _domain_name="C", _side_names="Gamma");
Geometry G=(S1^S2)-C; // intersection of spheres minus cylinder
At this stage, the geometry G handles only a symbolic description and does not handle any OCT object. It can be not dealt with usual mesh tools of XLiFE++ addressing only the standard gmsh engine. Now invoking the Mesh constructor with the mesh generator option gmshOC will produce the creation of OCT objects related to geometries involved (here spheres and cylinder) and an OCT object related to the geometry G that will be exported to Gmsh in a particular way.
Mesh M(G, _shape=triangle, _generator=gmshOC);

In this example, the name of domains created by Mesh are quite natural: “Sigma” and “Sigma_2” for the sphere boundaries and “Gamma” for the cylinder boundary. But in some more complex cases, it can be not so intuitive to recover domain names, especially when new faces are created. There is a quite simple way to recover them. Indeed, when meshing with gmshOC generator, 3 files are created in the folder containing the executable file:
- xlifepp.brep
-
containing the brep export of the OCT object
- xlifepp.geo
-
a gmsh script file containing the command to load the brep file and some additional commands related to mesh discretization and domain names.
- xlifepp.msh
-
the mesh file created by gmsh and loaded by XLiFE++ to create the
Meshobject.
Loading the xlifepp.geo in gmsh and configuring it to see curve/surface labels will allow you to identify easier domain names.
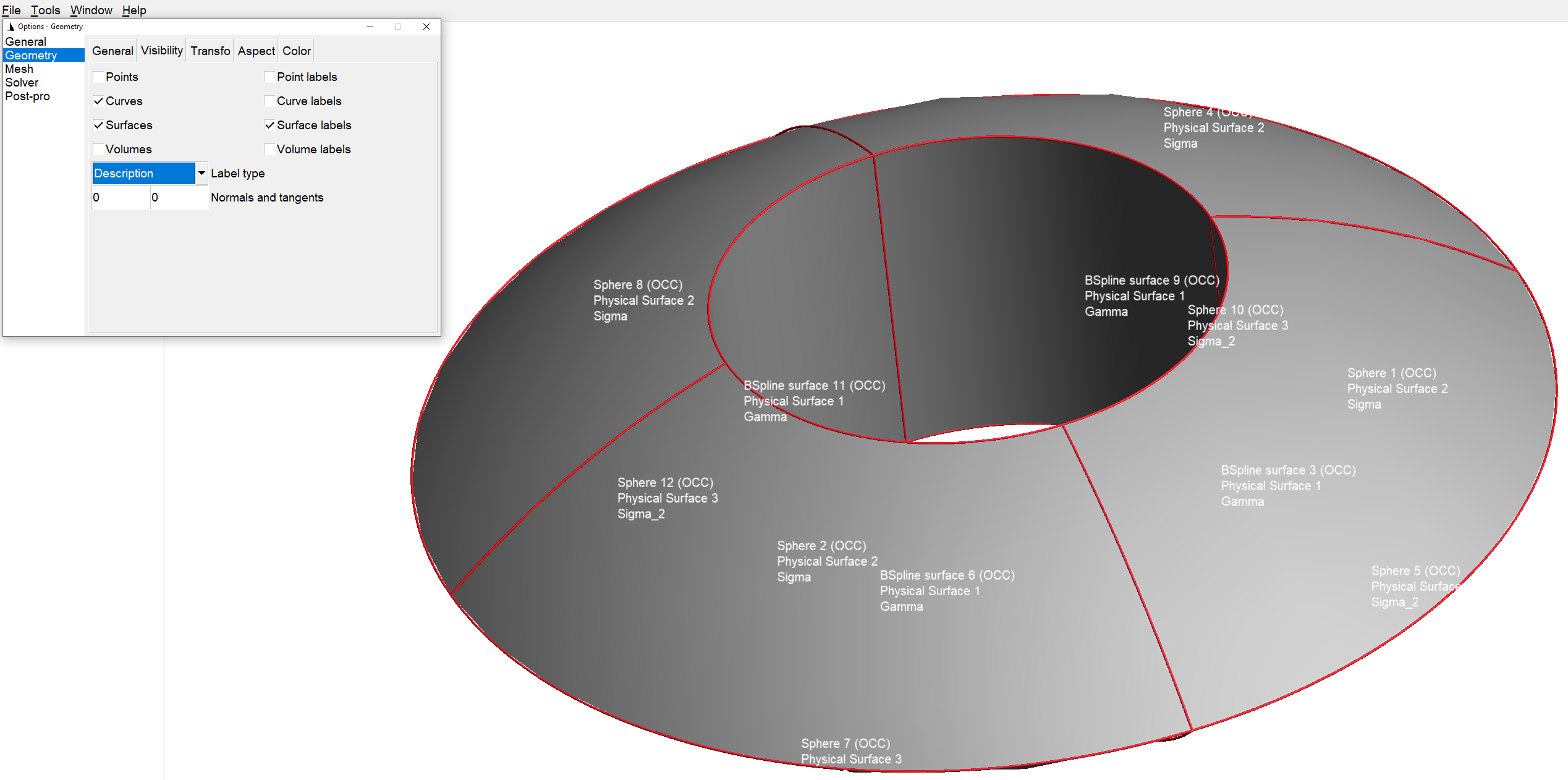
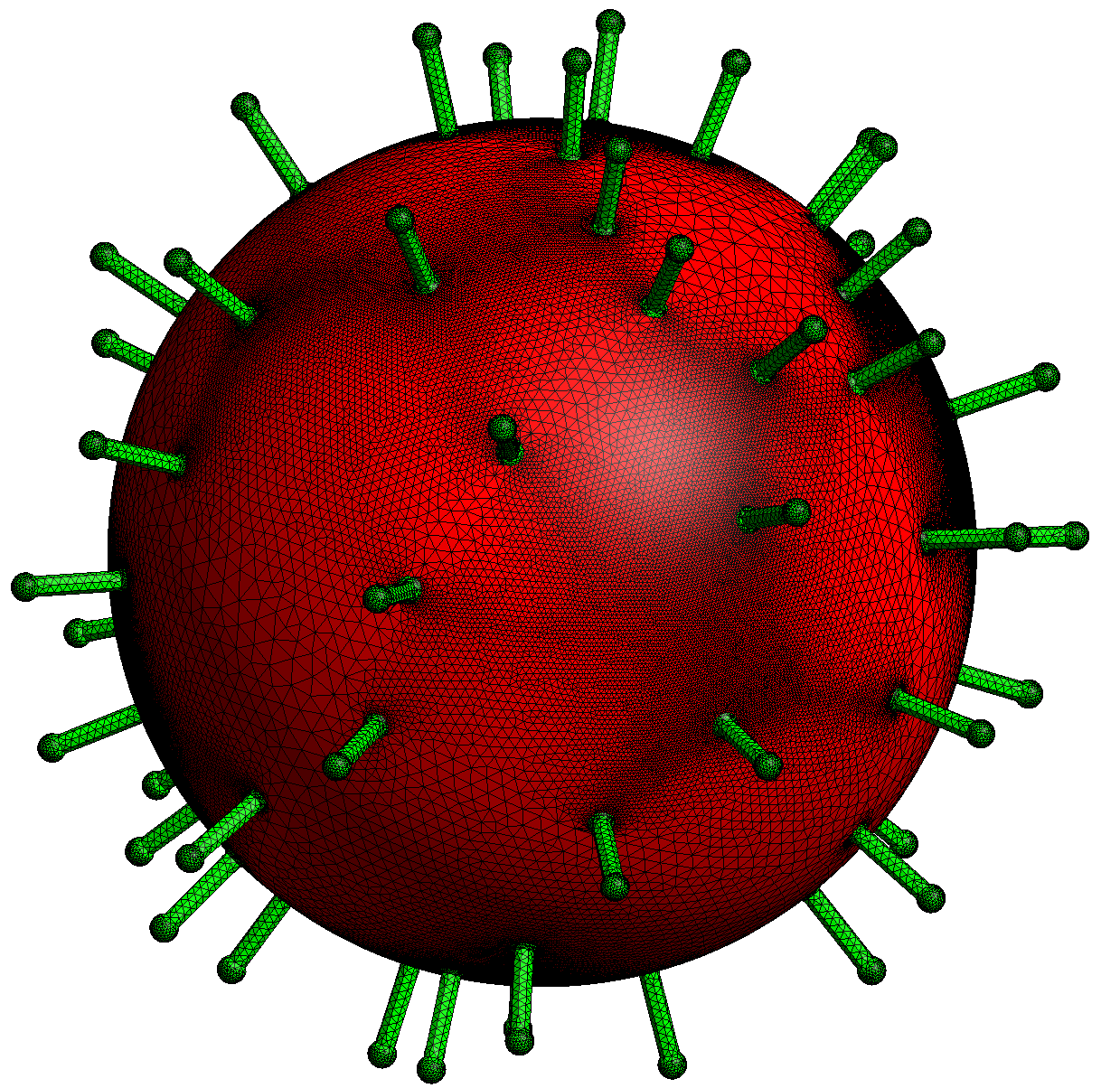
The next example shows how powerful is OCT and how XLiFE++ can manage complex geometries:
Cone co(_center1=Point(0.,0.,0.), _v1=Point(1.,0.,0.), _v2=Point(0.,1.,0.), _apex=Point(0.,0.,1), _hsteps=0.3,_side_names="gamma");
Cylinder cy(_center1=Point(0.,0.,0.), _v1=Point(0.7,0.,0.), _v2=Point(0.,0.7,0.), _center2=Point(0.,0.,7.), _hsteps=1,_side_names="gamma");
Sphere sp(_center=Point(0.,0.,7.), _radius=1., _hsteps=0.3,_side_names="gamma");
Geometry ant=cy+co+sp;
Real R=30., aR=0.999*R, d=0.2;
Sphere spcor(_center=Point(0.,0.,0.), _radius=R, _hsteps=2, _side_names="sigma");
Geometry cor=toComposite(spcor);
for (Number i=0; i<8; i++)
{
for (Number j=0; j<7; j++)
{
Real ir = i+d*(2*std::rand() * (1.0 / RAND_MAX)-1), jr= j+d*(2*std::rand() * (1.0 / RAND_MAX)-1);
Real t=pi_*(ir/4-1), p=pi_/8*(jr-3);
Transformation tf = Translation(_direction={aR*cos(t)*cos(p), aR*sin(t)*cos(p), aR*sin(p)}) * Rotation3d(_center=Point(0.,0.,0.), _axis={0.,0.,1.}, _angle=t);
tf *= Rotation3d(_center=Point(0.,0.,0.), _axis={0.,1.,0.}, _angle=pi_/2-p);
cor+=transform(ant, tf);
}
}
Mesh M(cor, _shape=triangle, _generator=gmshOC);
Available geometrical operations#
operation |
with OC extension |
standard geometry engine |
|---|---|---|
+ |
merge geometries (fusion) |
union of disjoint or included geometries |
- |
difference of geometries (cut) |
make a hole (included geometries) |
^ |
intersection of geometries (common) |
not available |
% |
not managed |
force inclusion |
Importing brep files#
OCT extension provides a new interesting feature : loading a BREP file in a Geometry object and mesh it using the gmshOC generator:
Geometry naca("NACA63-412.brep");
naca.setOCName(_solid, 1, "naca");
naca.setOCName(_face, 1, "extrados"); //extrados face
naca.setOCName(_face, 2, "intrados"); //intrados face
naca.setOCName(_face, Numbers(3,4), "lateral"); //lateral faces
naca.setOCHstep(Numbers(1,3), 0.2);
naca.setOCHstep(Numbers(2,4), 0.1);
Mesh(naca, _generator=gmshOC);
In this example, after viewing in gmsh the “NACA63-412.brep” file and identify numbers of elementary objects (solid, face, point), some particular functions (setOCName, setOCHstep, setOCNnode) allow controlling names and mesh size parameters.
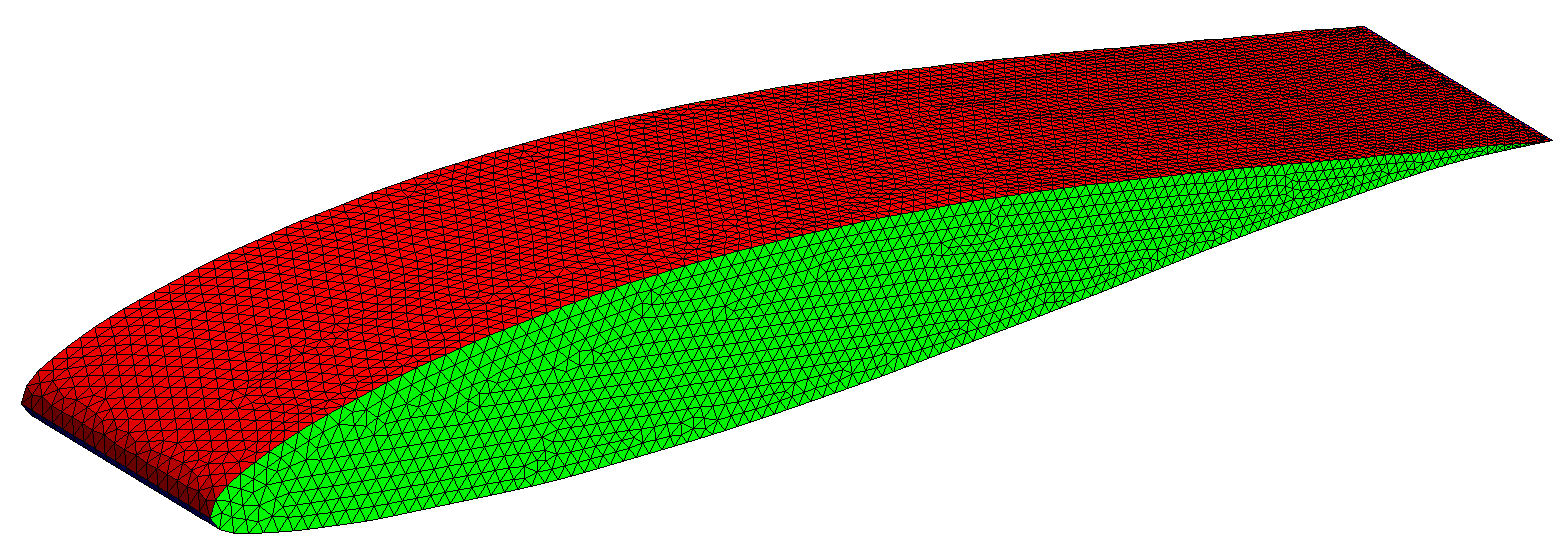
Extruding a mesh#
As an alternative to mesh an extruded geometry, it is possible to extrude a 1D or a 2D mesh, applying a Transformation (Translation, Rotation, …) using the routine extrude:
Mesh mdi(Disk(_center=Point(0.,0.), _radius=1., _nnodes=8), _shape=_triangle);
Mesh m=extrude(mdi, Rotation3d(_center=Point(3.,0.,0.), _axis={0.,1.,0.}, _angle=2*pi_/40), _layers=40);
Here a 3d rotation of angle \(\frac{\pi}{20}\) is applied to each section and _layers key-value specifies the number of layers (40). Note that in that case, a full turn is done and the last section coincides with the first section, the nodes being not duplicated.

Fig. 49 Extrusion using a rotation leading to a torus#
The transformation may be a basic transformation (translation, rotation, …) or a combination of transformations (see Transformations on points, geometries and meshes for more details). Instead of specifiying a transformation, it is also possible to specify the list of transformations to apply to the sections.
To deal with more general extrusions, a C++ function giving the parameterization of the extrusion path: \(t\in[0,1]\rightarrow \gamma(t)\in \mathbb R^d\) can be given.
Be caution, the parameterization has to statisfy \(\gamma(0)=0\) and \(\gamma'(0)=n_s\) where \(n_s\) is the normal vector to the section to be extruded.
By default, the rotation center \(C_0\) is the barycenter of all nodes of the section \(S_0\) but it can be changed using the key-value _center.
Note that this process guarantees that all sections are orthogonal to the extrusion curve.
Reals gamma(const Point& P, Parameters& par, DiffOpType dop)
{
Real t=P(1);
if (dop==_dt) return Reals{16*pi_*std::sin(4*pi_*t), 0., 40.};
return Reals{2*(1-std::cos(4*pi_*t)), 0., 40*t};
}
Mesh mdi(Disk(_center=Point(0.,0.), _radius=1., _nnodes=8), _shape=_triangle, _generator=subdiv);
Mesh m=extrude(mdi, gamma, _layers=100);

Fig. 50 Extrusion using a curve parameterization#
Tip
The orientation of normal vector to the section to be extruded is not predictable. But using the routine setNormalOrientation it can be set:
Mesh mdi(Disk(_center=Point(0.,0.), _radius=1., _nnodes=8), _shape=_triangle);
mdi.domain(0).setNormalOrientation(_towardsInfinite, Point(0.,0.,-1.));
where the given point (here (0.,0.,-1.)) specifies an ‘interior’ point.
Danger
If curvature radius is too small compared to the section size, the extrusion process may lead to incoherent domain!
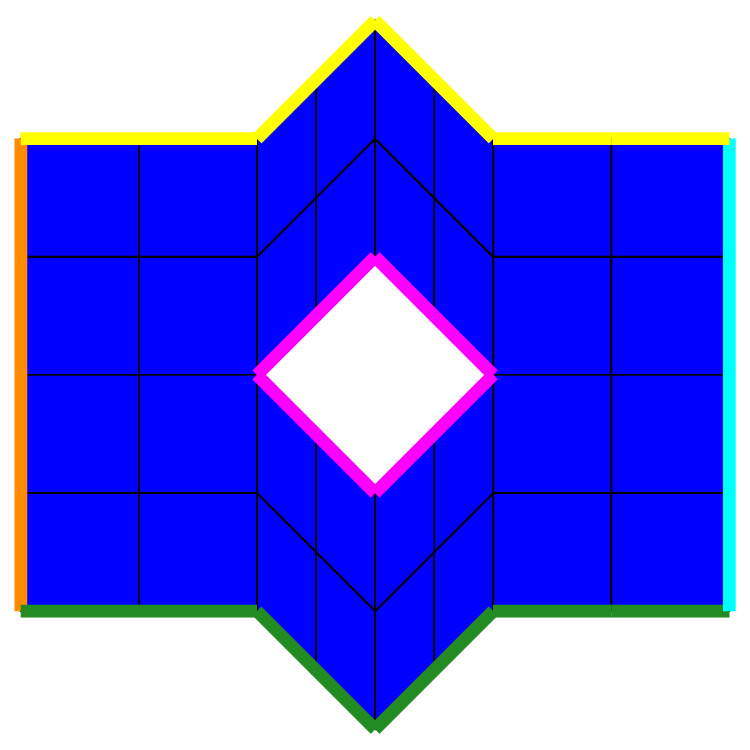
extrude manages the following key-values :
_layersto give the number of layers (mandatory)_centerto give the center of rotation when using a curve parameterization (computed by default)_init_transformationto specify a tranformation to apply to the reference section before extruding it (none by default)_naming_domainto control the naming of domains (noName,globalName,indexedName)_naming_sectionto control the naming of sections(noName,globalName,indexedName)_naming_sideto control the naming of boundaries (noName,globalName,indexedName)
The meaning of the naming arguments is
noName: no domains, section domains or boundaries domains are created. The full domain is always created and named “#Omega”.globalName: only some global extruded domains, a domain including end sections or some global boundary domains included all boundary domains are created (domain names are postfixed _e).indexedName: for each layer, one extruded domain, section domain or boundary domains are created (domain names are postfixed _0, _1,… or _e0, _e1, …).
The following picture illustrates the different ways to create and name the domains in extrusion process:
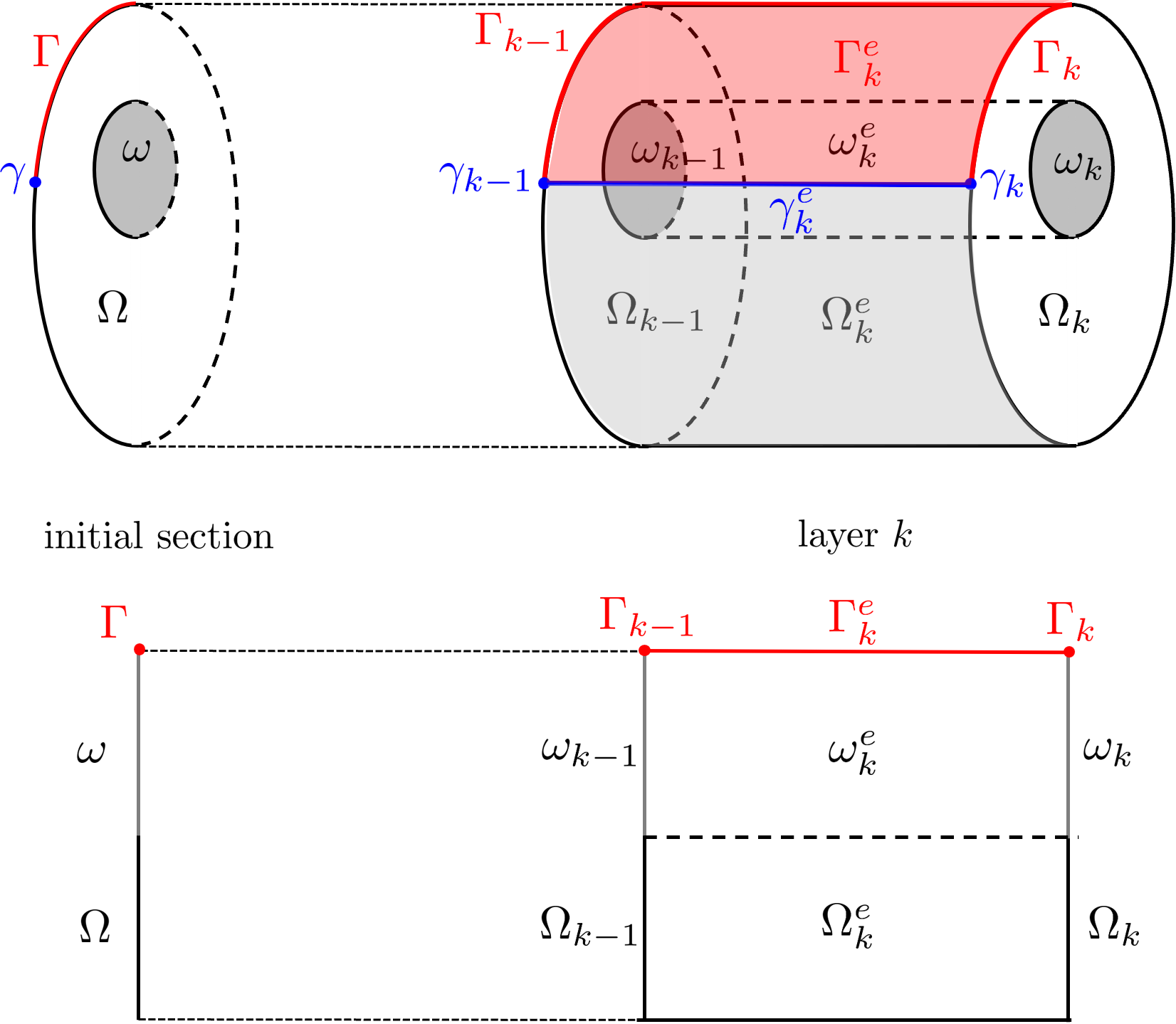

Be cautious, the side domains of extruded domain are created from the side domains of the given section. Thus, if the given section has no side domains, the extruded domains will have no side domain! For instance, to mesh a tubular domain using the mesh extrusion of a crown:
Disk dext(_center=Point(0.,0.), _radius=1., _nnodes=20, _domain_name="Omega", _side_names="Sigma");
Disk dint(_center=Point(0.,0.), _radius=0.5, _nnodes=10, _side_names="Gamma");
Mesh crown(dext-dint, _generator=gmsh);
Mesh tube(crown, Translation(_direction={0.,0.,1.}), _layers=10, _naming_domain=globalName, _naming_section=globalName, _naming_side=globalName);
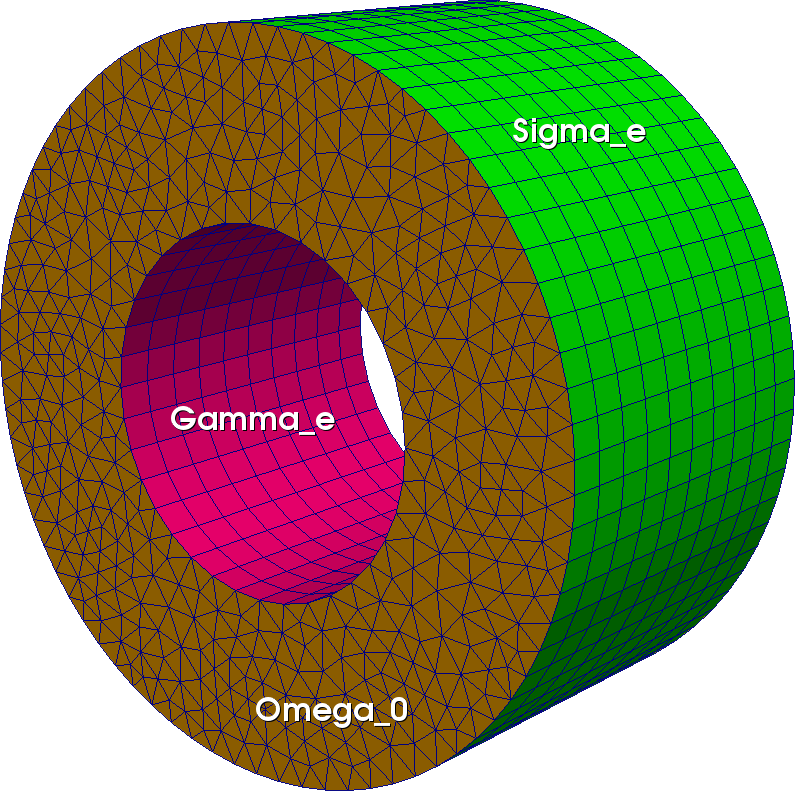
Fig. 51 Tube prismatic mesh from extrusion of a crown mesh#
See more details at Mesh extrusion.
Mesh refinement and splitting#
It is possible to refine an existing mesh of order 1: a new mesh is created using the subdivision generator mentioned above. The corresponding constructor is defined as follows:
Mesh m1(...);
//! Constructor from a mesh to be subdivided
Mesh m2(m1, _refinement_depth=2, _order=2);
This builds a mesh m2 which is obtained by subdividing twice the mesh m1, and changing the mesh order to 2.
The optional keys are:
_refinement_depth: the refinement depth of the subdivision generator. 0 means no refinement (the default value).
_order:the mesh order (defaut value is 1).
Sometimes it may be useful to split elements into elements of another type, for instance to produce mesh of pyramids that are not provided by standard meshing software products. To do this, the routine split is available:
Cuboid c(_xmin=0, _xmax=1, _ymin=1, _ymax=3, _zmin=1, _zmax=5, _nnodes=Numbers(3, 5, 9));
Mesh meshQ1(c, _shape=hexahedron, _generator=structured, _name="Q1 mesh of [0,1]x[1,3]x[1,5]");
Mesh meshPyramid=split(meshQ1, pyramid, "Py1 mesh of [0,1]x[1,3]x[1,5]");
Up to now, only one splitting process is available: hexahedron of order 1 into six pyramids of order 1. Note that a hexahedron is split into the six pyramids based on the hexahedron faces and the centroid of the hexahedron as tip.
Transformations on meshes#
Geometrical transformations on meshes work as on geometries. Please see Transformations on points, geometries and meshes for definition and use of transformations routines.
Then, if you want to apply a transformation and modify the input object, you can use one of the following functions:
translate to apply a translation
rotate2d to apply a rotation 2d
rotate3d to apply a rotation 3d
homothetize to apply a homothety
pointReflect to apply a point reflection
reflect2d to apply a reflection 2d
reflect3d to apply a reflection 3d
For instance:
Mesh m(...);
m.translate(_direction={0.,0.,1.});
However, if you want now to create a new Mesh by applying a transformation on a Mesh, you should use one of the related external functions instead.
For instance:
Mesh m(...);
Mesh m2=translate(m, _direction={0.,0.,1.});
Merging meshes#
Meshes of same dimension can be merged. They can share common parts or common boundaries but with same elements/nodes. If elements or nodes on common parts do not coincide,
the resulting mesh would not be conform to do finite element approximations. The merging process combines the elements and nodes of the meshes,
eliminating duplicate elements or duplicate nodes. Domains with same name are also merged, names being preserved. The new whole domain is created with default name #Omega or one given
and shared boundary domains are merged on demand (default). The merge function can deal with up to 5 meshes:
Mesh m = merge(m1,m2,[m3],[m4],[m5],[mergeSharedBoundary = true],[name = "#Omega"]);
As an exemple:
Rectangle R1(_xmin=0, _xmax=1, _ymin=1, _ymax=3, _nnodes={6,10});
Rectangle R2(_xmin=1, _xmax=2, _ymin=1, _ymax=3, _nnodes={3, 5});
Mesh mP1(R1, _shape=triangle, _generator=structured, _name="P1 mesh");
Mesh mQ1(R2, _shape=quadrangle, _generator=structured, _name="Q1 mesh");
Mesh mP1Q1 = merge(mP1,mQ1);
Rectangle R3(_xmin=1, _xmax=2, _ymin=1, _ymax=3, _nnodes={6,10});
Mesh mQ1a(R3, _shape=quadrangle, _generator=structured, _name="Q1 mesh a");
mP1Q1 = merge(mP1,mQ1a);
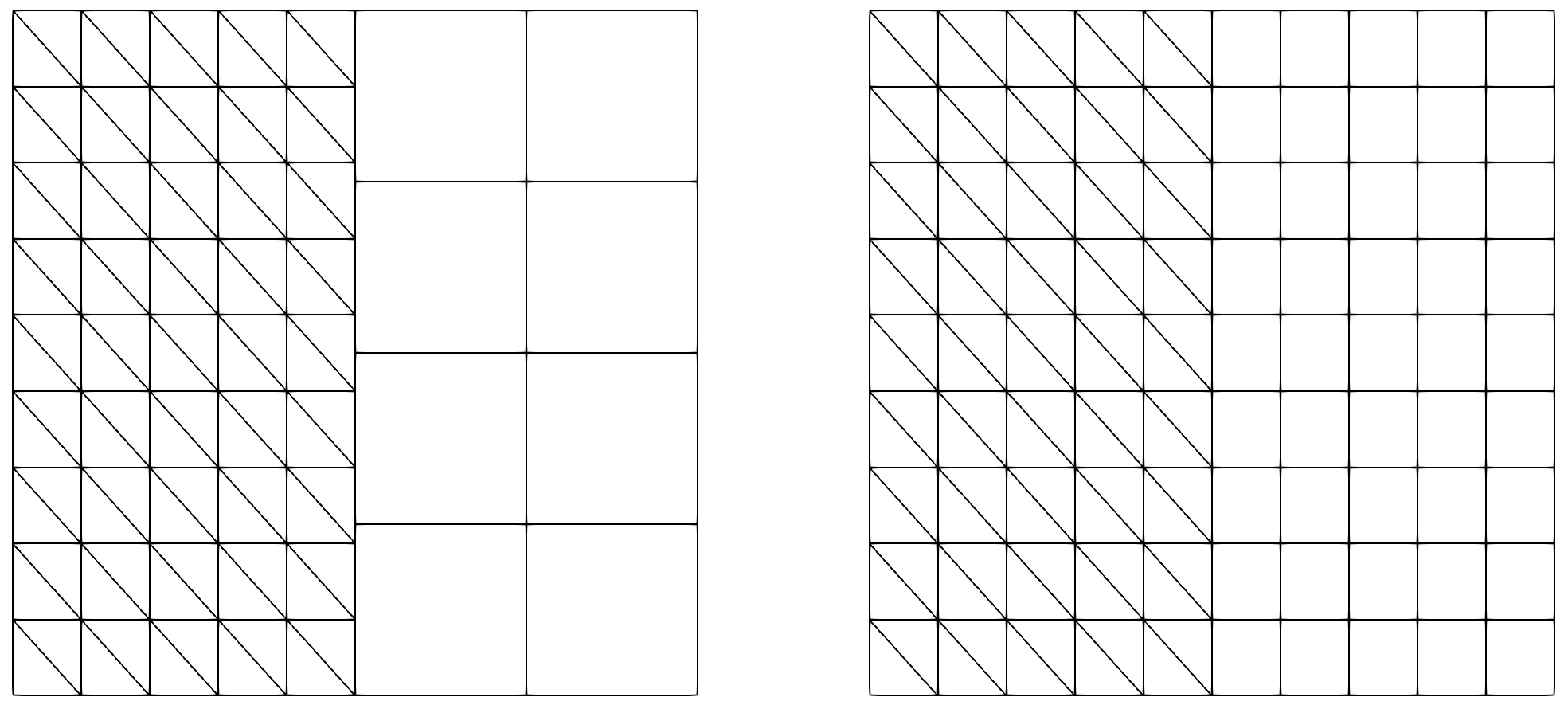
Fig. 52 Non-conforming and conforming merging of a triangular mesh with a quadrangular mesh.#
In merging process, the following rules are aplied:
all named domains of original meshes are preserved, with the same names,
if two different domains have the same name, say domname, they are merged, name being unchanged
if two side domains define an interface and have the same name, say domname, only one domain remains, again named domname and regarded as an interface.
-
if two side domains define an interface in the merging process and do not have the same name, say domname1 and domname2:
if
mergeSharedBoundaryis true, a new domain named domname1_domname2 is created and the original ones are deletedif
mergeSharedBoundaryis false, the original domains domname1 and domname2 are retained
As an exemple, consider two meshes with ‘g’ as side names except the interface \(\{1\}\times ]0,1[\) named ‘s’:
Rectangle R1(_xmin=0, _xmax=1, _ymin=0, _ymax=1, _nnodes={3,3},
_domain_name="omega",_side_names={"g","s","g","g"});
Mesh mR1P1(R1, _shape=_triangle, _order=1, _generator=_structured, _name="P1 mesh");
Rectangle R2(_xmin=1, _xmax=2, _ymin=0, _ymax=1, _nnodes={3,3},
_domain_name="omega", _side_names={"g","g","g","s"});
Mesh mR2Q1(R2, _shape=_quadrangle, _order=1, _generator=_structured _name="Q1 mesh");
Mesh mR1R2=merge(mR1P1,mR2Q1);
The merging process produces the following domains:
Domain 'omega' of dimension 2 from mesh 'P1 mesh + Q1 mesh', orientation not computed, 12 elements
geometric element 4 (material 0, color 0, twin 0): triangle_Lagrange_1, ...
geometric element 5 (material 0, color 0, twin 0): triangle_Lagrange_1,...
geometric element 6 (material 0, color 0, twin 0): triangle_Lagrange_1,...
geometric element 8 (material 0, color 0, twin 0): triangle_Lagrange_1,...
geometric element 9 (material 0, color 0, twin 0): quadrangle_Lagrange_1, ...
geometric element 10 (material 0, color 0, twin 0): quadrangle_Lagrange_1,...
geometric element 11 (material 0, color 0, twin 0): quadrangle_Lagrange_1,...
geometric element 7 (material 0, color 0, twin 0): triangle_Lagrange_1,...
geometric element 12 (material 0, color 0, twin 0): quadrangle_Lagrange_1,...
geometric element 2 (material 0, color 0, twin 0): triangle_Lagrange_1,...
geometric element 1 (material 0, color 0, twin 0): triangle_Lagrange_1,...
geometric element 3 (material 0, color 0, twin 0): triangle_Lagrange_1,...
Domain 'g' of dimension 1 from mesh 'P1 mesh + Q1 mesh', orientation not computed, 12 elements
geometric side element 14: side 3 of element 3
geometric side element 15: side 3 of element 8
geometric side element 13: side 3 of element 1
geometric side element 17: side 3 of element 6
geometric side element 21: side 1 of element 10
geometric side element 18: side 2 of element 1
geometric side element 22: side 2 of element 10
geometric side element 23: side 3 of element 12
geometric side element 16: side 2 of element 5
geometric side element 24: side 3 of element 11
geometric side element 25: side 2 of element 12
geometric side element 26: side 1 of element 9
Domain 's' of dimension 1 from mesh 'P1 mesh + Q1 mesh', orientation not computed, 2 elements
geometric side element 29: side 2 of element 4, side 4 of element 9
geometric side element 30: side 2 of element 8, side 4 of element 11
All domains are merged:
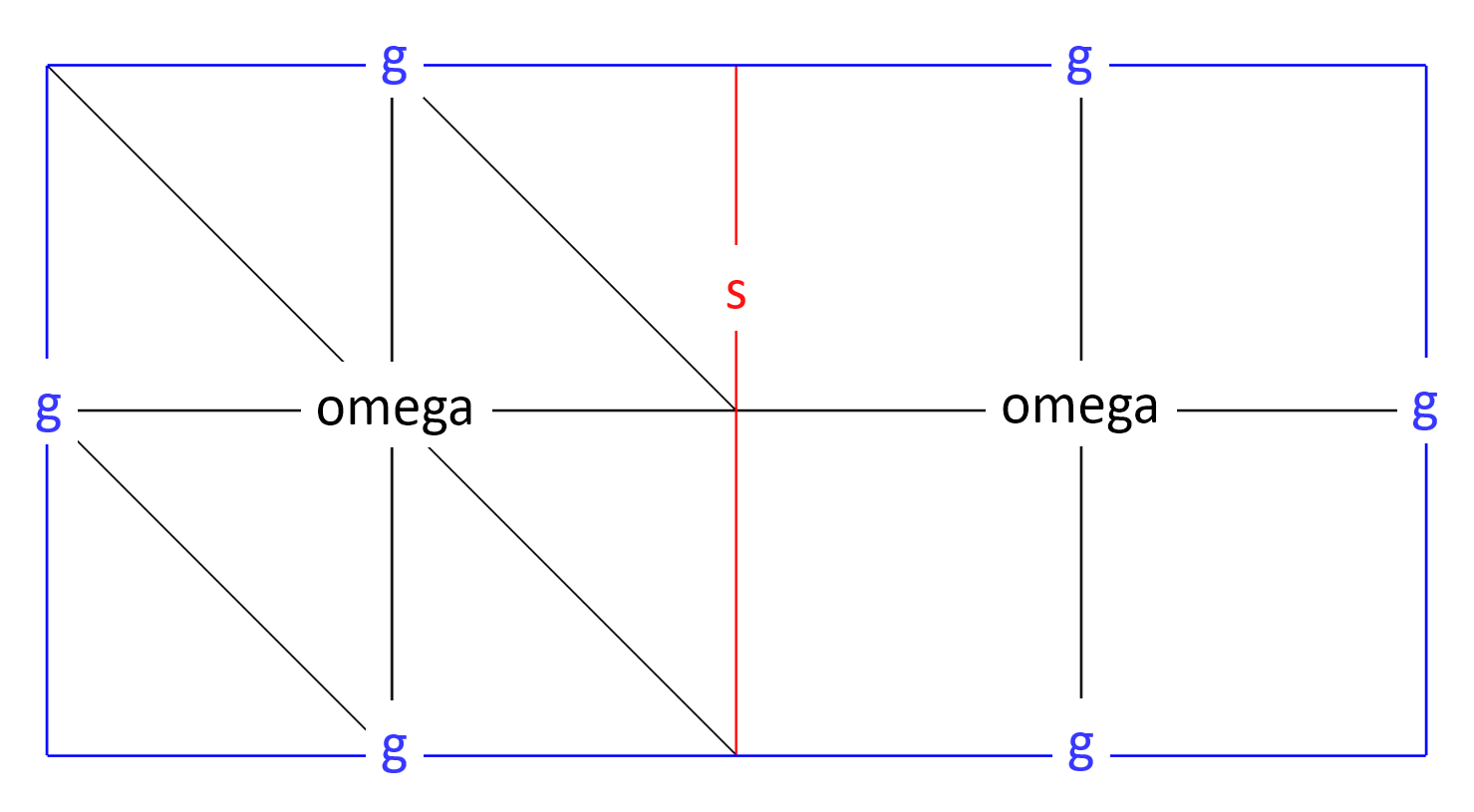
Fig. 53 Merging two meshes with same domain names.#
For additional details see Merging meshes.
How to display the mesh data ?#
Once a mesh is created, it is possible to get information about what it is made of using the function printInfo, which displays on the terminal general information about the mesh: characteristic data, domains, …:
Mesh m1("mesh.msh", _name="My Mesh");
m1.printInfo();
Particular mesh tools#
It may be useful to mesh a cone connected to an ellipsoid in a C1 way. It is provided the following function
Mesh RegularConeSphereTri(Point c, Reals ax, Real hc, Real rc, Real obl, Number nbs, Number nbb, MeshGenerator mg, Strings domNames, String interfaceName, Strings apexNames)
where
c is the center of the cone basis
ax is the cone axis vector
hc is the cone height
rc is the cone basis radius
obl is the oblateness of the sphere (1 means a sphere else an ellipsoid)
nbs is the number of sections of sphere and cone
nbb is the number of nodes on the basis of section of cone or sphere
mg is the mesh generator to use (_subdiv or _gmsh)
domNames is the list of domain names to give to the cone and the ellipsoid
interfaceName is the name of the interface between the cone and the ellipsoid
apexNames is the name of the cone apex and the sphere pole
The following exemples show how to use this function in the two cases of the subdivision generator and the gmsh generator:
Mesh meshConeSphere_subdiv = RegularConeSphereTri(Point(0.,0.,0.), Reals(0.,-1,0.), 4., 1, 0.5, 8, 17, _subdiv, Strings{"cone","sphere"},"circle",Strings{"apex","pole"});
Mesh meshConeSphere_gmsh = RegularConeSphereTri(Point(0.,0.,0.), Reals(0.,-1,0.), 4., 1, 0.5, 8, 17, _gmsh, Strings{"cone","sphere"},"circle",Strings{"apex","pole"});

The mesh obtained with the subdivision generator is more regular than the mesh obtained with the gmsh generator, but the latter is more balanced because the number of nodes on cone sides is adjusted according to the mesh size on the cone basis.That is not possible with the subdivision generator!
Note that only the surface is meshed with triangles, the volume is not meshed!
A full example with periodic cavities#
You want to mesh a rectangular domain, but on the bottom side of the rectangle, you want to have periodic cavities with the following pattern:

Definition of the cavity :
First, you have to define the first cavity, according to the previous figure:
// Definition of the cavity
Real l1=0.06, l2=0.04, l3=0.08, h1=0.05, h2=0.1, s=0.01;
Point po(1.,0.);
Point pa=po+Point(l1,0.), pb=pa+Point(0.,h1), pc=pb+Point(-l2,0.);
Point pd=pc+Point(0.,h2), pe=pd+Point(2.*l2+l3,0.), pf=pe+Point(0.,-h2);
Point pg=pf+Point(-l2,0.), ph=pg+Point(0.,-h1), pi=ph+Point(l1,0.);
Segment s1(_v1=po, _v2=pa, _hsteps=s), s2(_v1=pa, _v2=pb, _hsteps=s),
s3(_v1=pb, _v2=pc, _hsteps=s), s4(_v1=pc, _v2=pd, _hsteps=s),
s5(_v1=pd, _v2=pe, _hsteps=s), s6(_v1=pe, _v2=pf, _hsteps=s),
s7(_v1=pf, _v2=pg, _hsteps=s), s8(_v1=pg, _v2=ph, _hsteps=s),
s9(_v1=ph, _v2=pi, _hsteps=s);
Geometry cavity=s1+s2+s3+s4+s5+s6+s7+s8+s9;
When done, you can define the other cavities as results of translations of the first cavity:
// Definition of the cavities
Real cL=2.*l1+l3; // cavity length
Number nbcav=10; // number of cavities
Geometry cavities=cavity;
for (Number n=1; n<nbcav; n++) { cavities+=translate(cavity, _direction={n*cL,0.}); }
Finally, we define borders of the main domain, and mesh the resulting Geometry object defined with surfaceFrom:
// full geometry
Real sb=0.05;
Point p1(0.,0.), p2(2.+nbcav*cL,0.), p3(2.+nbcav*cL,1.), p4(0.,1.);
Segment s0(_v1=p1, _v2=po, _hsteps=Reals(sb, s)), s10(_v1=Point(1.+nbcav*cL,0.), _v2=p2, _hsteps=Reals(s, sb)), s11(_v1=p2, _v2=p3, _hsteps=sb, _domain_name="SigmaP"), s12(_v1=p3, _v2=p4, _hsteps=sb), s13(_v1=p4, _v2=p1, _hsteps=sb, _domain_name="SigmaM");
Geometry borders=s0+cavities+s10+s11+s12+s13;
// create mesh
Mesh mesh2d(surfaceFrom(borders,"Omega"), _generator=gmsh);
Domain omega=mesh2d.domain("Omega");
Domain sigmaP=mesh2d.domain("SigmaP");
Domain sigmaM=mesh2d.domain("SigmaM");