Problem definition#
Solving linear PDE problem with XLiFE++ is based on a variational formulation which handles a bilinear form, say \(a\) and a linear form, say \(l\), both defined on an approximation space \(V\) and having good properties (continuity, coercivity, …) to ensure the existence and uniqueness of solution:
In the context of XLiFE++, the space \(V\) may be either a Space or a product of Space \(V_i\), the unknown \(u\) a vector of unknowns \(u_i\)
and the associated test function \(v\) a vector of test functions \(v_i\). In first case, we speak of a single unknown formulation whereas it is a multiple unknowns formulation in the second case.
Please refer to Finite elements spaces and Unknowns and test functions to see how to define approximation spaces, unknowns and test functions.
Both bilinear and linear form may be linear combinations of single or double integrals involving operators on unknowns and, in the bilinear case, test functions. As integral are generally computed numerically, an integration method or a quadrature rule can be attached to integrals.
Examples to get you started#
XLiFE++ management of differential operators is as close as possible to the mathematical description, few operators are overloaded and a lot of possibilities are offered. It concerns either the variational formulation, or essential conditions. Here are some examples to understand how it works.
Laplace problem with Neumann condition#
The variational formulation to be solved here is: \(u\in V,\ \forall v\in V\)
Its implementation with XLiFE++ is:
...
BilinearForm auv = intg(omega, grad(u)|grad(v)) + intg(omega, u*v);
LinearForm lv = intg(omega, f*v) - intg(gamma, g*v);
The bilinear form \(a(u, v)\) is handled using a BilinearForm object and the linear form \(l(v)\) with a LinearForm object.
Please see Inhomogeneous coefficients below to learn how to manage functions f and g.
See 2D/3D Laplace problem with Neumann condition for the full example.
Laplace problem with Dirichlet condition#
The variational formulation to be solved here is: \(u\in G+V,\ \forall v\in V\) (\(G\) an extension of the Dirichlet data \(g\))
Implementation with XLiFE++ is:
...
BilinearForm auv = intg(omega, grad(u)|grad(v));
LinearForm lv = intg(omega, f*v);
EssentialConditions ecs = (u|gamma = g)
Here, an EssentialConditions object is used to take into account the non-homogeneous Dirichlet condition. The | restriction operator on a domain allows to define easily essential conditions.
See Essential conditions for more details.
See 2D Laplace problem with Dirichlet condition for the full example.
Helmholtz problem using single layer potential integral equation#
The variational formulation to be solved here is:
where \(\Gamma\) is the boundary of a 2D/3D bounded domain. The solution \(u\) is got from potential \(p\) from the integral representation:
where \(\Omega\) is the outside of the sphere.
Implementation with XLiFE++ is:
Kernel K=Helmholtz3dKernel(k);
IntegrationMethods ims(_method=SauterSchwab, _order=3, _quad=symmetricalGauss, _order=3);
BilinearForm auv = intg(gamma, gamma, p*K*q, _method=ims);
LinearForm lv = - intg(gamma, uinc*q);
Three new elements appear here:
The use of an already implemented kernel with a
Kernelobject. Please see the Available standard kernels.The definition of double integrals, taking 2 domains as arguments. The first concerns the test function part, the second concerns the unknown part.
The definition of a particular integration method for the Boundary Integral Equation Method : the Sauter-Schwab method of order 3 to manage the singularity part, and the symmetrical Gauss quadrature rule of order 3 for the regular part. See the Integration methods for more details.
See 3D Helmholtz problem using single layer potential integral equation for the full example.
Note
In variational formulation, the test function \(q\) is conjugated whereas it is not in the BilinearForm. This could be the case, but there would be no effect because FE basis functions are real-valued!
Maxwell equations#
The variational formulation to be solved in a \(H(curl)\) conform space is:
Implementation with XLiFE++ is:
...
BilinearForm aev=intg(omega, curl(e)|curl(q)) - omg2*mu*eps*intg(omega, e|q);
LinearForm l=intg(omega, f|q);
EssentialConditions ecs = (_n^e)|gamma=0);
Here, e and q are vectors and it appears the curl differential operator and the | operand (inner product). Here is also introduced the symbol _n for the normal vector.
See 2D Maxwell equations using Nedelec elements for the full example.
Elasticity problem#
The variational formulation to be solved here is:
Implementation with XLiFE++ is:
...
BilinearForm auv = lambda*intg(omega, div(u)*div(v)) + 2*mu*intg(omega, epsilon(u) % epsilon(v)) - w2*intg(omega, u|v);
LinearForm fv=intg(omega, f|v);
EssentialConditions ecs= (u|gamma=0);
Here, u and v are vectors. The epsilon operator defining the elasticity tensor and the % operand for the tensor inner product are new elements.
See 2D Elasticity problem for the full example.
Laplace Problem with Discontinuous Galerkin method#
The variational formulation to be solved in \(L^2\) conform space is:
where \(s\Omega\) is the set of sides of elements of \(\Omega\) (see Global operations on domains) and \(\mu\) is a penalty function usually chosen to be proportional to the inverse of the measure of the side \(S_{k\ell}\)
Implementation with XLiFE++ is:
...
BilinearForm a=intg(omega, grad(u)|grad(v)) - intg(somega, mean(grad(u)|_n)*jump(v))
- intg(somega, jump(u)*mean(grad(v)|_n)) + intg(somega, mu*jump(u)*jump(v));
LinearForm lv = intg(omega, f*v);
EssentialConditions ecs= (u|gamma = 0) & (ndotgrad(u)|gamma = 0);
New mean, jump and ndotgrad operators are introduced.
See 2D Laplace Problem with Discontinuous Galerkin method and Dirichlet condition for the full example.
Caution
jump and mean operators are to be used relatively to a domain of side elements (interface of domains or set of sides, see sidesDomain function). They must be interpreted on a side element \(S\) of two elements \(E_1\) and \(E_2\) as
where \(u_1=(u_{|E_1})_{|S}\) and \(u_2=(u_{|E_2})_{|S}\). The sign of jump is sensitive to the choice of the first element. Regarding the context, XLiFE++ may choose the right one, but it is not absolutely safe. Note that for DG approximations, generally the formulation is not sensitive to this choice. For instance
Note that the last expression is the way to take into account such DG term in XLiFE++.
Differential operators#
General syntax#
Differential operators are always built in the same way:
for single integrals (FEM case): an operator on the unknown
u, an operator on the test functionvand an algebraic operation between them.for double integrals (BEM case): an operator on the unknown
u, an operator on a kernelK, an operator on the test functionvand two algebraic operations between them.
An algebraic operand is one of the following:
the standard product, operator
*the inner product (hermitian product), operator
|the cross product, operator
^the tensor inner product, operator
%
For instance, where u denotes an unknown, v a test function, A a matrix, F a function and K a kernel:
mathematical expression |
XLiFE++ translation |
|---|---|
\(\nabla(u)\) |
|
\(\nabla(u)\cdot\nabla(v)\) |
|
\((A*\nabla(u))\cdot\nabla(v)\) |
|
\((F(x)*\nabla(u))\cdot\nabla(\overline{v})\) |
|
\(u(x)*K(x, y)*v(y)\) |
|
See Available differential operators to see the full list of differential operators (involving kernels or not).
Inhomogeneous coefficients#
Analytical functions#
General definition#
Defining analytical functions needs C++ functions with specific prototypes:
OUT f1(const Point& P, Parameters& pa = defaultParameters); // scalar form
Vector<OUT> f2(const Vector<Point>& Ps, Parameters& pa = defaultParameters); // vector form
The return type OUT can be one of the following: Real, Complex, Reals (or RealVector), Complexes (or ComplexVector), RealMatrix or ComplexMatrix.
The second input (Parameters object) can be used to manage additional parameters, such as a wavenumber, some lengths, or whatever you may need.
IF the Parameters is useless for you, you can use the C++ function directly in integrals:
Real f(const Point& P, Parameters& pa = defaultParameters)
{
return P(0)*P(1); // f(x,y)=x*y
}
...
LinearForm lv=intg(omega, f*v);
Functions with parameters#
Basic guidelines on parameters#
See The Parameter and Parameters classes to known how to use Parameters objects, but here are the main features:
-
A
Parametersobject is a list ofParameterobjects mapped by their names :// initialization of a Parameters pars with a Parameter k=2.5 Parameters pars(2.5, "k"); // adding/updating the Parameter nbpt=10 pars << Parameter(10, "nbpt");
A
Parametercan accept any object, either with standard types (See Basic types) or with more complex types, such asGeomDomain,Space, or even aTermVectorobject. In this case, you have to give the address of these objects:TermVector tv(...); pars << Parameter(&tv, "U");
-
To access a
Parameterobject containing a basic type, you can use theoperator():Real k = pars("k");
For more complex types, automatic conversion is not implemented, so you have to write the conversion by yourself by using
reinterpret_cast:TermVector& tv = *reinterpret_cast<const TermVector*>(pars("U").get_p());
Adding parameters to a function#
You can use a Function object to define a function with parameters. This object can be used in integrals
Real f(const Point& P, Parameters& pa = defaultParameters)
{
return P(0)*pa("k"); // f(x,y)=k*x
}
...
Parameters pars(...);
pars << ...;
Function F(f, pars);
LinearForm lv=intg(omega, F*v);
Updating a parameter associated to a function#
You can change the value of a parameter already assigned to a function object by using the setParam method:
Real f(const Point& P, Parameters& pa = defaultParameters)
{
return P(0)*pa("lambda"); // f(x,y)=\lambda*x
}
Parameters pars(2.5, "lambda");
pars << ...;
Function F(f, pars);
...
F.setParam(pi_, "lambda"); // update the value of parameter \lambda to 3.14
Managing normals and other running data in a function#
For advanced usage, you can access to running data related to the FE computation context where the function will be evaluated in an integral:
the current normal vector to the dommain: use
getN(orgetNxorgetNyin double integrals)the current tangent vector to the domain (
Reals&): usegetT(orgetTxorgetTyin double integrals)the current bitangent vector to the domain (
Reals&): usegetB(orgetBxorgetByin double integrals)the current domain (
Domain): usegetDomain(orgetDomainxorgetDomainyin double integrals)the material id (
Number): usegetMaterialIdthe current element (
GeomElement&): usegetElementthe current basis index (
Number): usegetBasisIndexthe current derivative index (
DiffOpType): usegetDerivative
To avoid type errors, use auto type to get correct references!
Caution
getNx, getNy, … have to be used in the context of double integral computations involving two geometric domains. When there is only one geometric involved, getNx returns the same vector as getN (same behaviour for the others functions).
By default, normal and tangent vectors may be not evaluated and therefore available in user function. If some vectors are required by the user’s function, this must be explicitly stated using the member function require:
Real f(const Point& P, Parameters& pa = defaultParameters) // C++ function
{
auto n = getN(); // get normal vector
return n(1)*P(1); // n.(x,0)
}
...
Function F(f); // XLiFE++ function
F.require(_n); // normal vector is required by f (unitary vector : _n, _nx, _ny, _tau, _taux, _tauy)
Interpolated functions#
Interpolated functions are functions defined from finite element approximation:
where \(w_i\) are some finite element shape functions and \(f_i\) are some real/complex scalar/vector coefficients. With Lagrange FE, \(f_i=f(x_i)\) where \(x_i\) is the node related to the shape function \(w_i\).
In XLiFE++ lib, such functions may be represented by TermVector objects that handle both a FE space, thus the shape functions, and the coefficients in an array of values. By specifying a TermVector object in an operator construction, an interpolated function will be handled.
Domain omega=...;
Space V(_domain=omega, _interpolation=P1, _name="V"); Unknown uh(V, _name="u");
TermVector x1(u, omega, _x1, "x1"); // interpolated function x
LinearForm l1=intg(omega, x1*u);
LinearForm l2=intg(omega, (x1^3)*u);
Such approach may be very useful for non-linear problem when non-linear terms are taken into account at a previous step in an iterative scheme.
Hint
For the moment, the way that XLiFE++ processes, consists in transforming the TermVector object in a Function object that performs the computation of the sum outside any context: first, it locates the finite element that contains the point x, then evaluates using local interpolation. As the localization algorithm has a log complexity, computation of the interpolated function at a point is not so time expansive, but it is not optimal, in particular when computing integral.
See Define interpolated values of an analytical function for more details on interpolated functions.
Kernels#
Defining analytical kernels requires also C++ functions with specific prototypes:
OUT k1(const Point& P, const Point & MParameters& pa = defaultParameters); // scalar form
Vector<OUT> k2(const Vector<Point>& Ps, const Vector<Point>& Ms, Parameters& pa = defaultParameters); // vector form
The C++ function can be directly used in integrals, or used to define a Kernel object such as
Kernel K(k1, "K", params);
A name can be given to a Kernel object and a Parameters object can be attached to.
Available standard kernels#
There are currently some kernels available in XLiFE++ for 2D and 3D problems: Laplace and Helmholtz Green functions, and Maxwell Green tensor in 3D:
-
The Laplace kernel used for 2D problems is
\[L_{2d}(x, y) = -\dfrac{1}{2 \pi} \log \left( \|x-y\| \right),\]and for 3D:
\[L_{3d}(x, y) = \dfrac{1}{4 \pi \|x-y\|}\] -
The Helmholtz Green function for 2D problems used is
\[H_{2d}(k, x, y) = \dfrac{i}{4} H_0^{(1)} \left(k \|x-y\|\right),\]with \(H_0^{(1)}\) the first kind Hankel function of order 0.
and for 3D:
\[H_{3d}(k, x, y) = \dfrac{e^{i k \|x -y\|}}{4 \pi \|x-y\|}.\] -
The harmonic Maxwell Green tensor for 3D problems is defined as:
\[M_{3d}(k, x, y)=H_{3d}(k, x, y) \mathbb{I}_3 + \dfrac{1}{k^2} \text{Hess}(H_{3d}(k, x, y)).\] The Green function for 2D Helmholtz problem in the strip \(]-\infty,+\infty[\times ]0,h[\) with Dirichlet or Neumann condition is also available. Its calculation is based on modal expansions (restricted to \(n\) first terms) if \(|x_1-y_1|>l\) and an accelerated image expansion else.
Examples of declaration of these kernels follow:
Kernel GLap2D=Laplace2dKernel();
Kernel GLap3D=Laplace3dKernel();
Parameters pars(k,"k"); // provide the wavenumber k using a Parameters
Kernel G=Helmholtz2dKernel(pars);
Kernel GHelm3D=Helmholtz3dKernel(k); // provide the wavenumber directly
Kernel GMaxw3Helm2DD=Maxwell3dKernel(k);
Kernel GMaxw3D=Maxwell3dKernel(k);
Kernel GHelm2DStrip= Helmholtz2dStripKernel(_Dirichlet, k, h, n, l, eps);
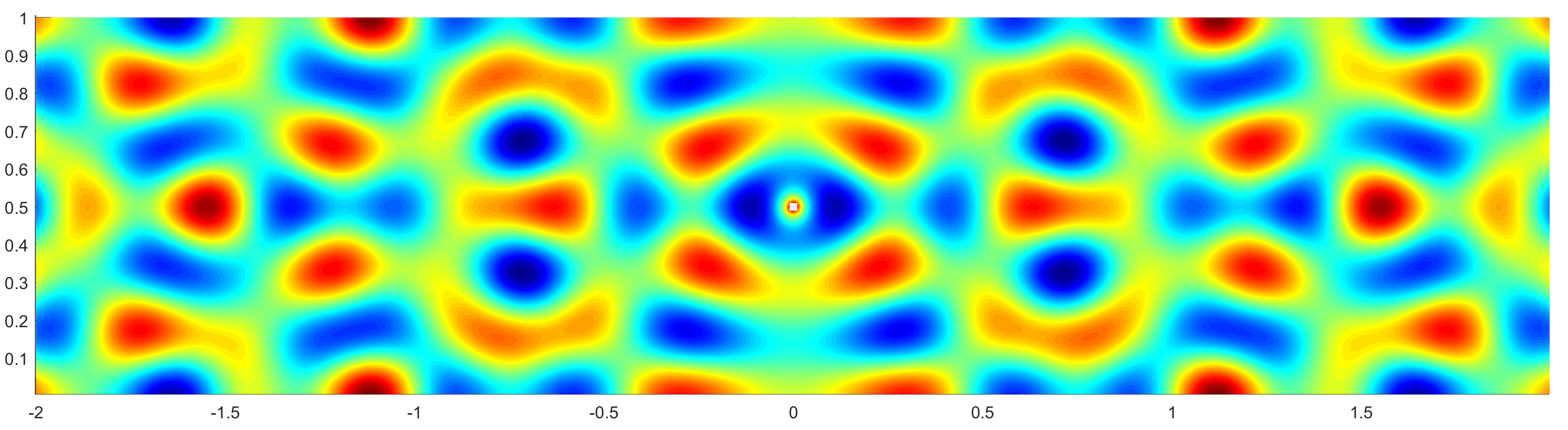
Fig. 56 Helmholtz 2D Green function in the strip \(]-\infty,+\infty[\times ]0,1[\) with \(k=20\) and Neumann condition#
Tensor kernels#
Tensor kernel is a kernel of the general form
It is involved in the so-called DtN operator (spectral expression), for instance:
where a related bilinear form could be
In that case, \(\mathbb{A}\) is a diagonal matrix (\(\mathbb{A}_{nn}=\lambda_n\)).
TensorKernel object can be constructed
from
SpectralBasisfrom
Unknownattached to a spectral spacefrom
Function(\(\varphi_n\) given analytically )from
TermVectors, a list ofTermVector(\(\varphi_n\) given as interpolated functions )
As an example, consider the construction of a TensorKernel from a given function or an unknown:
// spectral functions
Real sin_n(const Point& P, Parameters& pa = defaultParameters)
{
Real x = P.x();
Real h = pa("h"); // get the parameter h (user definition)
Number n = getBasisIndex(); // get the index of function to compute
return sqrt(2. / h) * sin(n * pi_ * x / h); // computation
}
...
Real h=1.; Number N=10;
Parameters ps(h., "h");
Vector<Complex> A(N); // diagonal matrix as a vector
for (Number n=0; n<N; n++) A[n]=sqrt(Complex(k*k-n*n*pi_*pi_/(h*h)));
//using Function
TensorKernel tk(Function(sin_n, "sin_n", ps),A);
//using Unknown attached to a spectral space
Space V(_domain=Omega, _basis=Function(sin_n, "sin_n", ps), _dim=N _name="sinus space");
Unknown phi(V,_name="phi");
TensorKernel tk(phi,A);
When the tensor kernel involves two basis, the second one corresponding to \(\psi_n\) is given after the matrix as a Function or an Unknown:
Function phi_n(sin_n, "sin_n", ps);
Function psi_n(cos_n, "cos_n", ps);
TensorKernel tk(phi_n, A, psi_n);
If the second basis functions involved in the tensor kernel must be conjugated, it can be done by specifying true as last argument of the constructor:
TensorKernel tk(Function(sin_n, "sin_n", ps), A, true);
Linear combination of differential operators (experimental)#
This new and experimental feature allows combining different operations on the unknown \(u\) and the test function \(v\) inside the same integral:
BilinearForm d = intg(omega, grad(u)|grad(v)) + intg(omega, u*v);
BilinearForm d = intg(omega, (grad(u)|grad(v)) + u*v); // new syntax
LinearForm l = intg(omega, v) + intg(omega, dx(v));
LinearForm l = intg(omega, v + dx(v)); // new syntax
It is even possible to factorize expressions:
BilinearForm d = intg(omega, (dx(u) + dy(u)) * v);
Hint
Because of the operation order induced by C++ language, parentheses must be added sometimes to help the interpretation of the integral by XLiFE++. This occurs frequently for low-priority C++ operation such as | and ^{}.
Additional operations on operators#
Transpose and conjugate#
Some quantities (function or kernel) involved in a bilinear form may have to be transposed or conjugated. XLiFE++ provides 3 operators to do it:
tranto transpose an expressionconjto conjugate an expressionadjto conjugate and transpose an expression
Obviously, transposition has only meaning for functions or kernels returning a matrix! In XLiFE++, the shape functions related to a FE space are real scalar/vector functions, so transpose or conjugate an unknown has no interest and, by the way, is not allowed!
Extension#
Some problems require dealing with the extension of a function/kernel, say \(f\) or \(k\), from a boundary (say \(\Gamma\)) to its parent domain (say \(\Omega\)). XLiFE++ provides a particular extension process that extends function/kernel from the boundary \(\Gamma\) to its neighborhood, that is the set of elements that have at least one vertex located onto \(\Gamma\), say \(\Gamma_{ext}\). More precisely, the extension formula is:
where \(M_i\) are some mesh vertices and \(w_i\) the one order Lagrange shape functions related to the vertex \(M_i\). Such extension vanishes outside \(\Gamma_{ext}\).
Define an extension is very easy. You have to specify the boundary domain to be extended, if not unique, the domain where you want to do the extension and the variable if you want to extend a kernel :
Extension Eg(Gamma); // extend from Gamma to elements in its neighborhood
Extension Eg(Gamma, _y); // extend from Gamma for variable y
Extension Eg(Gamma, Omega); // extend from Gamma to Omega
Extension Eg(Gamma, Omega, _x); // extend from Gamma to Omega for variable x
The set of elements in the neighborhood of \(\Gamma\) can be explicitly constructed by using the extendedDomain member function of Domain:
Domain Gamma_ext=Gamma.extendDomain(); // elements having a side on Gamma
Domain Gamma_ext=Gamma.extendDomain(true); // elements having a vertex on Gamma
Finally, to use extension in bilinear form, write for instance
Extension Eg(Gamma, Omega);
BilinearForm a=intg(Omega, u*Eg(f)*v); // extension of a function
Eg.var=_y;
BilinearForm a=intg(Gamma, Omega, u*Eg(k)*v); // extension of a kernel along y
Hint
The computations are automatically restricted to elements of the extended domain, so you do not have to restrict yourself. Be cautious, when applying an extension to an object involving kernel derivatives; for instance
Note
Don’t confuse local extension of function/kernel with global extension of a TermVector (see Extension).
Integration methods#
When defining a linear or a bilinear form, the user may specify the integration method or a list of integration methods to use, using either the _method key, or _quad and _order keys.
BilinearForm auv = intg(omega, grad(u)|grad(v), _quad=GaussLegendre, _order=3);
IntegrationMethods ims(_method=SauterSchwab, _order=3, _quad=symmetricalGauss, _order=3);
BilinearForm auv2 = intg(gamma, gamma, p*K*q, _method=ims);
Note that integration method is attached to the integral definition. So you can mix different integration methods in a bilinear form:
BilinearForm blf = intg(omega, grad(u)|grad(v), _quad=GaussLobatto, _order=1)
+ intg(omega, u*v, _quad=GaussLegendre, _order=2);
Using mixed integration methods is generally slower than using the same integration method!
Hint
It is not mandatory to specify an integration method in form; a default one is chosen according to the order of unknown interpolations, the order of differential operators involved and the fact that there are functions in operator on unknowns. For FE form, it is used the minimal quadrature rule for shapes involved in domain which integrates exactly the polynoms of order
where \(\DeclareMathOperator{\degop}{deg} \degop u\) (resp. \(\DeclareMathOperator{\degop}{deg} \degop v\)) is the degree of polynoms used by \(u\)-interpolation (resp. \(v\)-interpolation), \(\DeclareMathOperator{\order}{order}\DeclareMathOperator{\dif}{dif}\order \left(\dif u\right)\) (resp. \(\DeclareMathOperator{\order}{order}\DeclareMathOperator{\dif}{dif}\order \left(\dif v\right)\)) is the order of differential operator applied to \(u\) (resp. \(v\)) and \(\DeclareMathOperator{\order}{order} \DeclareMathOperator{\mesh}{mesh} \order(\mesh)\) the mesh order if greater than 1. [ ] means an optional coefficient.
Quadrature rules for single integrals#
Using _quad and _order keys is equivalent to use the _method key with a QuadratureIM object.
QuadratureIM quadIM(GaussLegendre, 2); // standard quadrature method
BilinearForm blf=intg(omega, uv, _method=quadIM);
BilinearForm blf=intg(omega, uv, _quad=GaussLegendre, _order=2); // shortcut syntax
To perform computation of integrals over reference elements, XLiFE++ provides a lot of quadrature formulae of the form:
where \((\widehat{x}_i)_{i=1,q}\) are quadrature points belonging to reference element \(\widehat{E}\) and \((w_i)_{i=1,q}\) are quadrature weights.
Up to now, quadrature formulae are implemented for unit segment \(]0,1[\), for unit triangle, for unit quadrangle (square), for unit tetrahedron, for unit hexahedron (cube), for unit prism and for unit pyramid.
See Available rules for the full list of available quadrature rules.
When bothh rule and degree are not given, the degree is determined by looking the degree of polynomials involved in the (bi)linearform taking into account derivative operators and the existence of an additional user function. For instance, the following bilinear form in \(P^k\) finite element space
will ask for a quadrature rule of degree \(d = 3k\) while the following bilinear form
will ask for a quadrature rule of degree \(d = 2*(k-1)\).
Once the degree \(d\) is determined, XLiFE++ chooses the best quadrature rule available for degree \(d\) and element shapes involved in the mesh domain. Generally for low degree (\(d \le 3\)) a specific rule is selected, for intermediate degree (\(4 \le d \le 10\)) a symmetrical Gauss rule is selected and for high degree a quadrature rule working at any degree (Gauss-Legendre or Grundman-Muller) is chosen.
See The best rules per shape and order to get more infomation on how the best rule (best in terms of number of quadrature points) is selected when only shape and degree are specified.
Hint
The user choice is always a priority even his choice leads to under integration. In doubt, let XLiFE++ works for you!
Integration methods for integral equation or integral representation#
Integral equation involves singular kernels. To deal with the singularity in integrals, some particular methods are proposed to users. LenoirSallesxx classes compute in an analytic way integrals involving 2D or 3D Laplace kernel but with low order finite elements (P0 or P1) whereas there are methods for any finite element order but specific problem dimension such as SauterSchwabIM for 3D problems and DuffyIM for 2D problems. Currently, only \(log(r)\) in 2D and \(r^{-1}\) in 3D singularities are addressed.
-
SauterSchwabIM[SaSch10]: -
This class addresses computation of integral
\[\int_{\Gamma} \int_{\Sigma} K(x,y) dx dy\]where \(\Gamma\) and \(\Sigma\) are 2D domains (in 3D) (partition of triangles) and \(K(x,y)\) a kernel having possibly a singularity of type \(1/||x-y||\). This technique is well adapted for most second order PDE in 3D. It uses a tensor product of four Gauss-Legendre quadrature on segment. When creating such method, you may specify the quadrature order on segment:
SauterSchwabIM ssIM(5);
The default order is \(3\). Sauter-Schwab method works for any finite element on triangle.
Hint
The Sauter-Schwab method consist in transforming the integral over a triangle pair to some integrals over the unity cube of \(\mathbb{R}^4\) and then computing each integral using a 4 tensor product of standard quadrature formula on segment. As a consequence, the number of points where the kernel is evaluated grows as a power 4 of the number of quadrature points used on segments. So increasing the order of quadrature on segment may be very time expansive.
-
DuffyIM[Du]: -
This class addresses computation of integral
\[\int_{\Gamma} \int_{\Sigma} K(x,y) dx dy\]where \(\Gamma\) and \(\Sigma\) are 1D domains (in 2D) (partition of segments) and \(K(x,y)\) a kernel having possibly a singularity of type \(\log(\|x-y\|)\). This technique is well adapted for most second order PDE in 2D. Duffy transform is used to compute integrals involving segments sharing only one vertex (say adjacent elements) and \(t^p\) transform method is used to compute self-influence coefficients (same segments). By default, \(p=5\).
When creating such method, the quadrature order on segment may be specified. The default order is 6. It is possible to specify different orders and to choose different quadrature orders depending on whether the case is adjacent or self-influence:
// GaussLegendre of order 10 on x and of order 8 on y DuffyIM dufIM(10,8);
The default order (for direction \(x\) or \(y\)) is 6. A full constructor allows specifying different quadratures regarding the directions \(x\) or \(y\), the geometrical configuration of both segments (self influence or adjacency), the order p of \(t^p\) transform. For instance, to use a very accurate quadrature (required in case of P2 curved element):
// GaussLegendre rule of order 20 for self influence on x and y // and GaussLegendre rule of order 60 for adjacency on x and y // and p=7 DuffyIM dufim(GaussLegendre, 20, GaussLegendre, 20, GaussLegendre, 60, GaussLegendre, 60, 7);
Duffy method works for any finite element on 1D element.
Hint
The
DuffyIMclass addresses only singular configurations. User has to provide some regular quadratures for regular configurations. -
LenoirSalles2dIMandLenoirSalles3dIM[LeSa12]: -
These classes address computation of integral
\[\int_{\Gamma} \int_{\Sigma} p(x) K(x, y) q(y) dx dy\]or
\[\int_{\Gamma} \int_{\Sigma} p(x) \partial_{n_y} K(x, y) q(y) dx dy\]where \(\Gamma\) and \(\Sigma\) are 2D domains in 3D (partition of triangles) or 1D domains in 2D (partition of segments), \(K(x,y)\) the Laplace kernel and \(p\), \(q\) are either piecewise constant functions or piecewise linear functions. It deals only the case of elements sharing at least one vertex. So for elements that are not close to, a standard quadrature has to be used. These classes do not manage any parameter:
LenoirSalles3dIM ls2; LenoirSalles2dIM ls3;
-
LenoirSalles2dIRandLenoirSalles3dIR: -
These classes address computation of integral
\[i(x)=\int_{\Gamma} K(x, y) q(y) dy\]or
\[i(x)=\int_{\Gamma} \partial_{n_y} K(x, y) q(y) dy\]where \(\Gamma\) is either a 2D domain in 3D (partition of triangles) or a 1D domain in 2D (partition of segments), \(K(x,y)\) the Laplace kernel and \(q\) is an either piecewise constant function or piecewise linear function. These classes do not manage any parameter:
LenoirSalles3dIR ls2; LenoirSalles2dIR ls3;
-
CollinoIM: -
This class is a wrapper to an integration method developed by F. Collino to deal with some integrals involved in 3D Maxwell BEM when using Raviart-Thomas elements of order 1 (triangle). More precisely, it can compute the integrals:
\[\DeclareMathOperator{\divop}{div} \int_{\Gamma} \int_{\Gamma} \left(k H(k, x, y) w_j(y) \cdot w_i(x)-\dfrac{1}{k} H(k, x, y) \divop w_j(y) \divop w_i(x)\right)\]and
\[\int_{\Gamma} \int_{\Gamma}\left(\nabla_y H(k, x, y)\times w_j(y)\right) \cdot w_i(x),\]where \((w_i)_{i=1,n}\) denote the Raviart-Thomas shape functions and \(H(k, x, y)\) the Green function of the Helmholtz equation (wave number k) in the 3D free space. For instance, to compute the first integral, write
Space RTh(_domain=Gamma, _interpolation=RT_1, _name="RTh"); Unknown U(RTh, _name="U"); TestFunction V(U, _name="V"); IntegrationMethods imc(_method=CollinoIM(_computeI1, 3, 64, 12, 3.)); Kernel H = Helmholtz3dKernel(k); BilinearForm ac = intg(Gamma, Gamma, k*(U*H|V) - (1./k)*(div(U)*H*div(V)), _method=imc); TermMatrix S(ac);
Use this syntax ONLY in this context! The parameters involved in the
CollinoIMobject correspond to the default values.
Define several integration methods#
Computing integral with kernel is a costly business because of the kernel singularity. But in fact, this singularity is effective only in particular situations: when two elements share at least one vertex in BEM computation or when the point is too close to an element in IR computation. This is the reason why XLiFE++ provides a way to choose different integration methods regarding a geometrical criterion: the relative distance between the centroids of elements.
or the relative distance between a point and the centroid of element
The IntegrationMethods class collects integration methods with two additional information:
the bound value \(b\) telling the integration method is applied when \(dr\leq b\)
the part of the function concerned by the integration method
Here are given some classical definitions of IntegrationMethods:
IntegrationMethods ims1(_method=SauterSchwab, _order=3, _quad=defaultQuadrature, _order=5);
IntegrationMethods ims2(_method=Duffy, _order=5, _quad=GaussLegendre, _order=10, _bound=1., _quad=GaussLegendre, _order=5, _bound=2., _quad=GaussLegendre, _order=3);
IntegrationMethods ims3(_method=LenoirSalles3d, _quad=GaussLegendre, _order=5);
IntegrationMethods imsh(_method=LenoirSalles2dIR(), _functionPart=singularPart, _bound=theRealMax, _quad=QuadratureIM(GaussLegendre, 4), _functionPart=regularPart, _bound=theRealMax);
For instance, the definition of ims2 corresponds to the following choice:
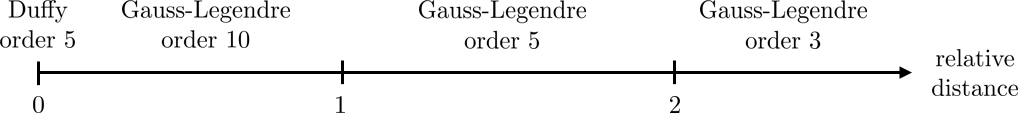
Warning
Beware of the definition of an IntegrationMethods object. In particular, check that all the cases are handled.
Everything is controlled by a key-value system, using keys inside the following set:
_method dedicated to integration methods for integral equation or integral representation
_quad dedicated to standard quadrature rule type
_order for the integration method order
_bound for the bound value telling the integration is applied when relative distance between elements is lower than this bound value
_functionPart for the part of the function concerned by the integration method. Possible values are allFunction (the default), regularPart and singularPart.
To define several integration methods, you have to use these keys several times, let’s say several “sets” of these keys. Here are the guidelines to these sets:
Each set must start with either
_methodkey or_quadkey. When XLiFE++ detects one of these keys, it considers a new set of keys is starting.As
_methodis dedicated up to now for integration methods on singular parts and_quadfor regular part, you should not need to use_functionPartkey.When
_methodis used, the default value of_boundis 0 (meaning auto-influence)When
_quadis used, the default value of_boundistheRealMax(meaning \(+\infty\))The default value of
_orderis set according to the default value of each integration method.-
Sets can be defined in any order. They are automatically sorted by
_boundand_functionPart. In the following example,ims1,ims2andims3are rigourously identical.IntegrationMethods ims1(_method=Duffy, _order=5, _quad=GaussLegendre, _order=10, _bound=1., _quad=GaussLegendre, _order=5, _bound=2., _quad=GaussLegendre, _order=3); IntegrationMethods ims2(_method=Duffy, _order=5, _quad=GaussLegendre, _order=5, _bound=2., _quad=GaussLegendre, _order=3, _quad=GaussLegendre, _order=10, _bound=1.); IntegrationMethods ims3(_quad=GaussLegendre, _order=10, _bound=1., _method=Duffy, _order=5, _quad=GaussLegendre, _order=5, _bound=2., _quad=GaussLegendre, _order=3);
Advanced usage of bilinear forms and linear forms#
Additional keys#
Some additional options are available in BilinearForm definition:
_symmetry-
to force the symmetry of the resulting matrix. Possible values are
symmetric,skewSymmetric,selfAdjoint,skewAdjoint, ornoSymmetrySpace sp(_domain=omega, ...); Unknown u(sp, _name="u", _dim=3); TestFunction v(u, _name="v"); BilinearForm b2 = intg(omega, (A*u)|v, symmetric); // explicit symmetry (supposing A symmetric)
Often, bilinear forms are some linear combination of integrals and the symmetry may result of the sum of non-symmetric integrals. In such cases, it is possible to force the symmetry by using the following syntax:
Space sp(_domain=omega, ...); Unknown u2(sp, _name="u2"); TestFunction v2(u2, _name="v2"); BilinearForm d = intg(omega, dx(u2)*dy(v2))+intg(omega, dy(u2)*dx(v2)); // considered as non-symmetric d.symType()=symmetric; // defined as symmetric
Caution
Be cautious, the usage of
symType()is restricted to single unknown bilinear forms! _isogeo-
To activate the use of isogeometric finite elements (experimental). This key does not take any value.
_computation-
For advanced usage, computation engine to use may be chosen. Possible values are:
FEComputation,IEComputation,SPComputation,FESPComputation,IESPComputation,FEextComputation,IEextComputation,IEHmatrixComputationorDGComputation _diagonal-
to build a diagonal matrix related to the bilinear form. This can be done only for Lagrange FE with Lobatto points:
Mesh msh(Rectangle(_xmin=0,_xmax=1,_ymin=0,_ymax=1,_hsteps=dx),_shape=_quadrangle,_order=1); Domain omg=msh.domain("Omega"); Space V(_domain=omg,_FE_type=Lagrange,_FE_subtype=GaussLobattoPoints,_order=k,_name="V"); Unknown u(V, _name="u"); TestFunction v(u, _name="v"); BilinearForm a = intg(omega, u*v, _diagonal); // to build a diagonal matrix
Using a Gauss-Lobatto quadrature of order \(2(k+1)-3\) leads also to a diagonal matrix:
BilinearForm a = intg(omega, u*v, _quad=GaussLobatto, _order=2*(k+1)-3);
Hint
Keep in mind that unknowns and test functions represent shape functions of the space which are real functions! Thus, there is no reason to conjugate test functions.
Define bilinear form involving unknowns on different meshes#
It is possible to deal with a single integral involving unknowns on different meshes. Consider the following XLiFE++ example:
Rectangle rect(_xmin=-1, _xmax=1, _ymin=-1, _ymax=1, _hsteps=0.1, _domain_name="Omega");
Mesh meshR(rect);
Segment seg(_v1=Point(-2./3,1./3), _v2=Point(2./3,1./3), _hsteps=0.1, _domain_name="Gamma");
Mesh meshS(seg);
Domain omega=meshR.domain("Omega");
Domain gamma=meshS.domain("Gamma");
Space V(_domain=omega, _interpolation=P1, _name="V");
Unknown u(V, _name="u"), TestFunction v(u, _name="v");
Space S(_domain=gamma, _interpolation=P0, _name="S");
Unknown p(S, _name="p"), TestFunction q(p, _name="qv");
BilinearForm a=intg(gamma, u*q);
The test function q is consistent with the domain gamma because q belongs to the FE space S defined from gamma, but u is not, because gamma is not related to the space V. Nevertheless, XLiFE++ can deal with by constructing a “fictitious” domain (named “gamma_F_omega”) made of elements of omega intersecting gamma.
It works also with two domains of same dimension:
Rectangle rect(_xmin=-1, _xmax=1, _ymin=-1, _ymax=1, _hsteps=0.1, _domain_name="Omega");
Mesh meshR(rect);
Rectangle rect_i(_xmin=-0.5, _xmax=0.5, _ymin=-0.5, _ymax=0.5, _hsteps=0.1, _domain_name="Omega_i");
Mesh meshRi(rect_int);
Domain omega=meshR.domain("Omega");
Space V(_domain=omega, _interpolation=P1, _name="V");
Unknown u(V, _name="u"); TestFunction v(u, _name="v");
Domain omegai=meshRi.domain("Omega_i");
Space Vi(_domain=omegai, _interpolation=P1, _name="Vi");
Unknown ui(Vi, _name="ui"); TestFunction vi(ui, _name="vi");
BilinearForm ai=intg(omegai, u*vi);
Dealing with non-standard bilinear form#
In some cases, the bilinear form to be dealt with, cannot be expressed using standard operators of XLiFE++ or involved operations that are not yet available in XLiFE++. This section explains how to use the UserBilinearForm class that handles bilinear form managing particular function doing the computation of elementary matrices.
For such bilinear form, the matrix computation algorithms bypass the quadrature machinery used classically and call the function attached to UserBilinearForm object.
First, a function computing the elementary matrices have to be defined. It has the following prototype:
void bfFun(BFComputationData& bfd)
{ ... }
where the BFComputationData class handles some information related to the elements concerned by the elementary matrix computation:
class BFComputationData
{
public:
const Element* elt_u, *elt_v; // never null pointer (FEM)
const Element* elt_u2, *elt_v2; // may be null pointer
const GeomElement* sidelt; // may be null pointer (DG case)
RealMatrix* matel; // real elementary matrix (pointer)
ComplexMatrix* cmatel; // complex elementary matrix (pointer)
}
elt_u, elt_v are pointers to some finite elements. They may be different if unknown space and test function space are different or if it is a BEM bilinear form (double integral). elt_u2, elt_v2 are pointers to other finite elements when more are involved.
This is the case of discontinuous Galerkin computation on a side element (sidelt) shared by elt_u and elt_u2. From elt, there is an access to the underlying GeomElement
object that handles the GeomMapData giving access to the geometric map from reference element to actual geometric element; in particular the jacobian matrix, the inverse of jacobian matrix,
the differential element can be extracted from this object. The following simple example shows how to compute the elementary matrix related to \(\nabla u \cdot \nabla v\) when using 2D P1 finite element:
void bfGradGrad(BFComputationData& bfd)
{
if (bfd.matel==0) bfd.matel=new RealMatrix(1,1); // allocate if not yet allocated
const Element* elt=bfd.elt_u;
if (elt==0) return; // no computation
GeomMapData& md = *elt->geomElt_p->meshElement()->geomMapData_p; //geometric map
Real dx=0.5*md.differentialElement;
RealMatrix& invJ=md.inverseJacobianMatrix;
RealMatrix C=dx*invJ*tran(invJ);
RealMatrix G(2,3,0.);
G(1,1)=1; G(2,2)=1; G(1,3)=-1; G(2,3)=-1; // gradient of 2D-P1 shape functions
*bfd.matel=tran(G)*C*G;
}
Danger
Here, pointers and references to XLiFE++ objects are explicitely used, so be careful.
Hint
Other information can be extracted from element, see Element class.
Once the function computing the elementary matrix is given, the user bilinear form can be defined:
Mesh ms(Rectangle(_xmin=0., _xmax=1., _ymin=0., _ymax=1., _nnodes=10, _domain_name="Omega"), _generator=structured, _split_direction=alternate);
Domain omega=ms.domain("Omega");
Space V(_domain=omega, _interpolation=P1, _name="H");
Unknown u(V, _name="u"); TestFunction v(u, _name="v");
bool invJ=true, nor=false;
BilinearForm ubf=userBilinearForm(omega, u, v, bfGradGrad, FEComputation, symmetric, invJ, nor);
The bilinear form is constructed using the userBilinearForm function indicating
The geometric domain concerned (or two domains if a double integral),
the unknown and test function involved,
the function computing elementary matrices,
the type of computation :
FEComputation,IEComputation,DGComputation,a symmetry property :
noSymmetry,symmetric, …,a boolean telling if the inverse of jacobian must be computed and a boolean telling if the normal vector must be computed.
The user bilinear form can be used as other bilinear forms. For instance to compute the related matrix associated to:
BilinearForm ubf=userBilinearForm(omega, u, v, bfGradGrad, FEComputation, symmetric, invJ, nor);
TermMatrix K(ubf, "K");
Note that the matrix K related to the user bilinear form ubf is the same as the one obtained using the standard bilinear form intg(omega, grad(u)|grad(v)).
Using H-matrices#
With H-matrices, matrices are represented by a hierarchical tree, each tree node being either a real submatrix (leaf) or a virtual submatrix addressing up to four nodes:
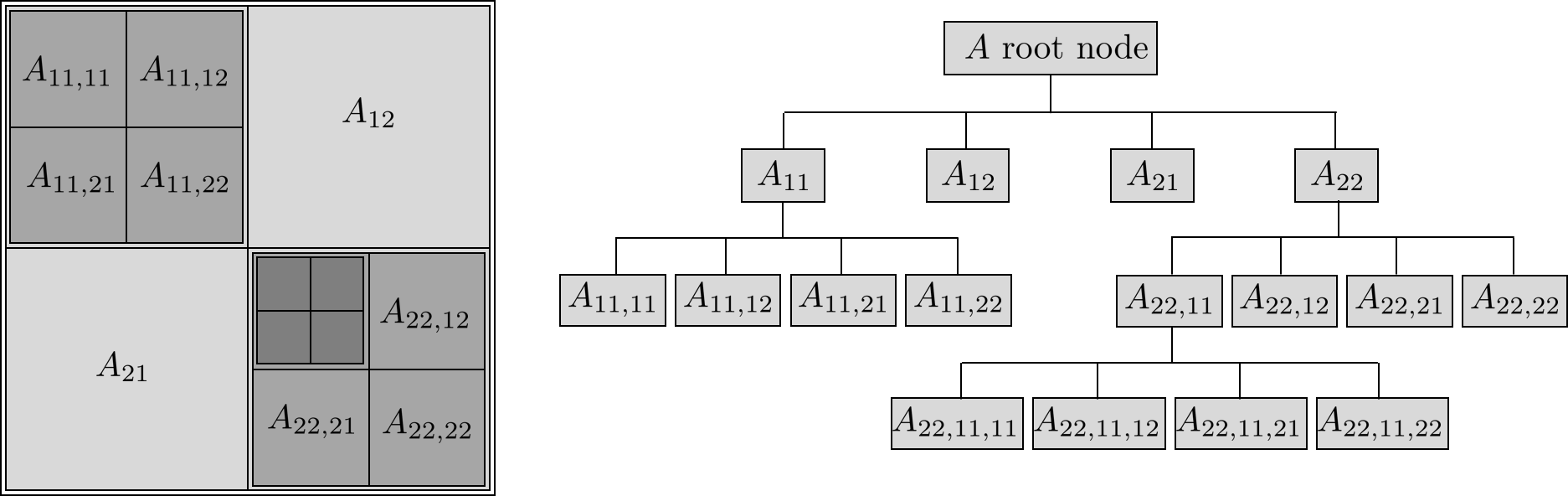
Fig. 57 Hierarchical matrix#
The matrix may be not squared and therefore the submatrices too.
Such representation comes from mesh partition (clustering) where far interactions in BEM may be approximated by low rank matrices, so reducing the storage of matrix and making the matrix vector product faster.
Using H-matrices is giving a HMatrixIM object to the key _method. To define a HMatrixIM object, you may use some of the following keys:
Essential conditions#
Essential conditions are conditions that appear in spaces involved in variational problem. These are constaints on unknown and test functions. The most common one is the Dirichlet condition on a boundary : \(u=0\) on \(\Gamma\) (homogeneous) or \(u=g\) on \(\Gamma\) (non-homogeneous). But there are others: transmission condition on a boundary, periodic condition between two boundaries, null average on a domain, … XLiFE++ provides a symbolic description of such conditions based on operator’s stuff already described.
The general syntax of an essential condition is the following
where
a1,a2are some constants\(\otimes\) is any algebraic operator: (
* | % ^)op1,op2are some operators on unknownu1,u2are some unknownsD1,D2are some domainsfis a constant or a function
Some classic scalar expressions are:
Homogeneous Dirichlet condition:
u|D = 0,Non-homogeneous Dirichlet condition:
u|D = f,Homogeneous transmission condition:
u1|D - u2|D = 0,Homogeneous periodic condition:
u|D1 - u|D2 = 0,Quasi periodic condition (
gfunction):u|D1 - g * u|D2 = 0
Obviously, syntax supports more conditions than the program can really deal with!
Warning
As the operator priority rules are the C++ rules, omitted parenthesis may induce some hazardous compilation errors. In doubt, use parenthesis.
To declare essential condition, users have to instantiate EssentialConditions object, which handles a set of conditions:
Strings sn("y=0", "y=1", "x=0", "x=1");
Mesh mesh2d(SquareGeo(_origin=Point(0.,0.), _length=1, _nnodes=10, _side_names=sn), _generator=structured);
Domain omega=mesh2d.domain("Omega");
Domain sigmaM=mesh2d.domain("x=0");
Domain sigmaP=mesh2d.domain("x=1");
Space V(_domain=omega, _interpolation=P1, _name="V");
Unknown u(V, _name="u");
EssentialConditions ecs = (u|sigmaM = 1);
Note
BoundaryConditions can be used instead of EssentialConditions (alias).
These conditions may use analytical functions or interpolated functions:
Real un(const Point& P, Parameters& pa = defaultParameters)
{ return 1.; }
EssentialConditions ecs = (u|sigma = un);
TermVector tvun (u, sigma, un);
EssentialConditions ecs2 = (u|sigma = tvun); // with an interpolated function
To concatenate conditions, use the operator & :
EssentialConditions ecs = (u|sigmaM = 1) & (u|sigmaP = 1) ;
It is possible to mix conditions. Here is a case with two unknowns related by a transmission condition:
...
Domain sigmaM=mesh2d.domain("x=0");
Domain sigmaP=mesh2d.domain("x=1");
Domain gamma=mesh2d.domain("x=1/2- or x=1/2+");
Space VM(_domain=omegaM, _interpolation=P2, _name="VM");
Unknown uM(VM, _name="u-");
Space VP(_domain=omegaP, _interpolation=P2, _name="VP");
Unknown uP(VP, _name="u+");
EssentialConditions ecs = (uM|sigmaM = 1) & (uP|sigmaP = 1) // Dirichlet
& ((uM|gamma) - (uP|gamma) = 0); // transmission
To deal with periodic condition, the map related to the two domains involved is required:
Vector<Real> mapPM(const Point& P, Parameters& pa = defaultParameters)
{
Point Q(P);
Q(1)-=1;
return Q;
}
...
Domain omega=mesh2d.domain("Omega");
Domain sigmaM=mesh2d.domain("x=0");
Domain sigmaP=mesh2d.domain("x=1");
Domain gammaM=mesh2d.domain("y=0");
Domain gammaP=mesh2d.domain("y=1");
Space V(_domain=omega, _interpolation=P1, _name="V");
Unknown u(V, _name="u");
defineMap(sigmaP, sigmaM, mapPM);
EssentialConditions ecs = (u|gammaM = 0) & (u|gammaP = 0) // Dirichlet
& ((u|sigmaP) - (u|sigmaM) = 0); // periodic
Hint
XLiFE++ uses a very powerful process to deal with essential condition: all constraints are merged in a unique linear constraints’ system which is reduced using a QR algorithm. This process is able to detect redundant or conflicting constraints. When some are redundant, they are deleted. When some are in conflict, they are also deleted but the right-hand side related components are averaged. For instance, this occurs when two Dirichlet conditions are not compatible at the intersection of two boundaries. In both cases a warning message is handled. It is the responsibility of user to check possible conflict.
Warning
Eliminating redundant conditions is based on a test in QR algorithm. More precisely, the QR process stops when the pivot coefficient is below a tolerance factor (by default \(100\times \varepsilon_{mach}\approx 2.10^{-14}\) in double precision). Sometimes, this default tolerance factor may be too small and some quasi redundant conditions are not reduced; leading to quasi ill posed linear system. To force the reduction of quasi redundant conditions, this tolerance factor may be increased:
EssentialConditions ecs = (ncross(ud)-ncross(ug)|Sigma=0);
ecs.redundancyTolerance(1.E-10);
Hint
Contrary to the mathematical point of view, in XLiFE++ the essential conditions are NOT attached to spaces but to algebraic representation of bilinear forms (see next section). This choice avoids defining multiple spaces.
To take into account constraints in the algebraic system, XLiFE++ offers several methods:
pseudo-elimination, not changing the size of the system but may be the storage (default)
elimination , decreasing the size of the system and changing the storage
penalization, not changing the storage but impacting the matrix conditionning (restricted)
dualization, indreasing the size of the system by adding some matrix blocks (not yet available)
See Deal with essential conditions for details.
Attention
Dealing with essential conditions may be time consumming, in particular when dealing with null average condition which impacts all the matrix coefficients when using elimination methods.
Advanced usage:
Most of essential conditions (except moment condition) are expressed as punctual relations. More precisely, the symbolic expression \(op(u)_{|D}\) is translated as
When using a Lagrange approximation, points \(M_i\) are the support of the Lagrange DoFs belonging to the domain \(D\). When non Lagrange element are concerned, virtual point supports, often defined in the reference element, are used. If there is no virtual point support, mesh nodes of the domain are used.
Using points that are shared by two elements (vertices for instance) may cause some troubles when operator or approximation involved is not continuous across element. To bypass this difficulty, it is possible to use internal points of elements instead of boundary points by modifying the property ecMethod of the essential condition:
EssentialCondition ec = (ncross(u)|gamma = 0);
ec.ecMethod = _internalNodeEC;
EssentialConditions ecs = ec;
Attention
Do not confuse EssentialCondition dealing with only one condition and EssentialConditions dealing with several conditions.
Using internal nodes generates more punctual relations than using DoF points, but the reduction process deals with very well.
