Solvers

Linear variational problems lead to algebraic sytems expressed in terms of TermMatrix and Vector, either linear systems: \(\mathbb{A}U=B\) or as eigenvalue problems: \(\mathbb{A}U=\lambda\,U\) and \(\mathbb{A}U=\lambda\,\mathbb{M}U\). XLiFE++ provides a wide set of linear system solvers (direct or iterative) and eigen solvers (built-in solvers or arpack solvers). The following sections explains some simple steps to make use of these solvers.

Direct Solvers

Because direct solvers involve some costly algorithms to solve very large linear systems through LDLt or LU factorization, a prerequisite to call them is to have TermMatrix factorized. It can be done as follows:

TermMatrix LD;        // Create a new TermMatrix to store factorized matrix
ldltFactorize(A, LD); // LDLt−Factorize

Then the linear system is solved in a next step:

TermVector U = factSolve(LD, B);

The TermVector X is returned as a solution of the solver. Or a TermMatrix can be factorized into LU before being solved

TermMatrix LU;      // Create a new TermMatrix to store factorized matrix
luFactorize(A, LU); // LU−Factorize
TermVector X = factSolve(LD, B);

Factorization and solving may be called in one time:

TermVector X = luSolve(A, B);

The available factorizations and direct solvers are

• LDLt factorization and solver (for symmetric matrix): functions ldltFactorize(), ldltSolve()

• LDLstar factorization and solver (for self-adjoint matrix): functions ldlstarFactorize(), ldlstarSolve()

• LU factorization and solver (for any matrix): functions luFactorize(), luSolve()

• umfpack factorization and solver (for any matrix) if umfpack is installed and configured: umfpackFactorize(), umfpackSolve()

• gauss elimination with pivoting for matrix stored in dense format: gaussSolve()

• Schur method on 2x2 TermMatrix : schurSolve()

• lapack solver for matrix stored in dense format if lapack is installed and configured: lapackSolve()

• magma solver for matrix stored in dense format if magma lib is available: magmaSolve()

LDLt, LDLstar and LU factorizations move matrix to skyline storage and may fail even if the matrix is invertible (no pivoting strategy)! Umfpack is most powerful because it works with compressed sparse storage and has pivoting strategy, but it may be slow.

Be sure of symmetry property of the matrix before calling LDLt or LDLstar methods. If not, call generic direct solver functions factorize, factSolve or directSolve which performs tests before calling the well adapted method:

TermMatrix Af;    // create a new TermMatrix to store factorized result
factorize(A, Af); // factorize the TermMatrix
TermVector X = factSolve(Af, B);  //solve factorized linear system

TermVector X = directSolve(A, B);  //same in one call

The behaviour of directSolve is the following:

• if matrix is dense : use lapack solver if available else use XLiFE++ Gauss solver,

• if matrix is sparse (compressed or skyline) use umfpack if available else use XLiFE++ factorization method.

Note that direct solver may induce storage conversion of the TermMatrix. By specifying true as last argument of solver functions, the input matrix is preserved:

TermVector X = directSolve(A, B, true); //keep original matrix

The right hand side is never modified.

Note

UmfPack solver is generally faster than XLiFE++ solvers except for block matrices (multiple unknowns), where the dynamic numbering optimization may be costly. In addition, the UmfPack solver is not multithreaded. Lapack solver may be slower than the XLiFE++ Gauss solver if non optimized lapack-blas libraries are used.

Note

Linear solvers fail when the modulus of a pivot coefficient is below a tolerance (\(\approx 2\, 10^{-16}\) in double precision). This means that the factorization algorithm is not applicable and probably that the matrix is singular.

Most solvers support multiple right-hand sides given as a TermVectors or a std::vector<TermVector:

TermVectors Bs;
...
TermVectors Xs = directSolve(A, Bs);

The factSolve and directSolve functions can also be used with a TermMatrix right hand side, say \(B\). Thus they produce a TermMatrix which is \(A^{-1}B\). Even both the matrices \(A\) and \(B\) are sparse matrix, the matrix \(A^{-1}B\) is not sparse. It is stored using a column dense storage.

TermMatrix Id(M1,_idMatrix,"Id");  // create Id matrix with M1 characteritics
TermMatrix invM1=directSolve(M1,Id,_keep); // create inverse of M1
TermMatrix invM1=inverse(M1);              // direct way to create inverse of M1

Note that inverse(M1) is strictly equivalent to directSolve(M1,Id,_keep). Because the result is stored in dense format, do not use on very large matrices (risk of memory overflow).

Warning

Up to now, the usage of factSolve, directSolve functions with a TermMatrix as right hand side and inverse() is restricted to single unknown TermMatrix.

Iterative solvers

In contrast to direct solvers, iterative methods approach the solution gradually, rather than in one large computational step. Up to now, there are several built-in iterative solvers:

• Conjugate Gradient (CG, CGS, BiCG, BiCGStab)

• Generalized Minimal RESidual (GMRes, Standard or Restarted)

• Quasi Minimal Residual (QMR)

• Successive Over Relaxation (SOR, SSOR)

These methods can be called with a preconditioner (SOR and SSOR excepted)

Define a preconditioner

To define a preconditionner, use the class PreconditionerTerm:

TermMatrix A=...;
Real omega=...;
PreconditionerTerm precond(A,_ssorPrec, omega);

The PreconditionerTerm constructor takes 3 arguments:

• the matrix used to build the precondition matrix.

• the type of preconditioner. Possible values are:

  • _luPrec, _iluPrec: the precondition matrix will be a (incomplete) LU factorization of the input matrix given

  • _ldltPrec, _ildltPrec: the precondition matrix will be a (incomplete) LDLt precondition of the input matrix given

  • _ldlstarPrec, _ildlstarPrec: the precondition matrix will be a (incomplete) LDL* precondition of the input matrix given

  • _ssorPrec: the precondition matrix will be a SSOR precondition of the input matrix given

  • _diagPrec: the precondition matrix will be a diagonal precondition of the input matrix given

  • _embeddedPrec: the precondition matrix will be the input matrix given, with no transform (default value)

• The relaxation parameter when SSOR precondition is used; its default value is 1.0.

Call an iterative solver

To invoke an iterative solver and make use of it, the easiest way is to call external functions:

TermVector U = iterativeSolve(A, B, _solver=_cg); // Solve with default initial guest X0=0

The available solvers (through their keys to the _solver parameter) are: _bicg, _bicgstab, _cg, _cgs, _gmres and _qmr.

There are shortcuts specific to each solver:

TermVector U = cgSolve(A, B);

The available functions are bicgSolve(), bicgStabSolve(), cgSolve(), cgsSolve(), gmresSolve(), qmrSolve(). They all call the general function iterativeSolve(). All these functions take parameters in the following orders:

• the matrix A (TermMatrix)

• the right hand side B (TermVector)

• optionally the initial guess X0 (TermVector)

• optionally the preconditioner P (PreconditionerTerm)

• optionally one or more key-value parameters, among the following:

  • _solver: only for routine iterativeSolve(). This parameter is not optional.

  • _tolerance: tolerance of the iterative solver. Default value is 1e-4 on 32 bits configurations, 1e-8 on 64 bits configurations.

  • _maxIt: maximum number of iterations. Default value is relative to the size of the linear system.

  • _verbose: verbose level (default value is 0, nothing printed).

  • _name: the name of the TermVector solution computes by the routines (default value is “U”).

  • _omega: only for routines sorSolve() and ssorSolve(), the relaxation parameter (default value is 1).

  • _krylovDim: only for routine gmresSolve(), the krylov dimension. Default value is the size of the linear system (for use of Standard GMRes). If it is set and lesser than the maximum number of iterations, it will be the* restarted* GMRes.

An advanced use of solvers would be to instantiate an iterative solver object and call it using operator():

CgSolver mySolver;               // Define an iterative solver object
TermVector U = mySolver(A,B,X0); // Solve the system with initial guess X0

For iterative solver objects, it can be used the same keys as seen prevously (_solver excepted, as it is meaningless here).

CgSolver mySolver(_tolerance=1.e-04, _maxIt=20);
TermVector U = mySolver(A,B,X0); // Solve the linear problem

In this example, the tolerance is made looser than default, to get faster a solution with an error of \(10^{-4}\). Nevertheless, the solver will cease after 20 iterations even if the solution has not been converged.

It is a big disadvantage of the iterative solvers: they do not always “just work”. Different problems do require different iterative solver settings, depending on the nature of the governing equation being solved. However, the advantage of the iterative solvers is their memory usage, which is significantly less than a direct solver for the same sized problems and resolution time, which can be drastically reduced by using a high tolerance factor. Look at the example “Helmholtz problem with CG solver” to know more how to write code with iterative solvers.

Advanced usage

The usage of iterative solvers presented above concerns TermMatrix and TermVector objects. This may be not adapted to some situations where the operators involved are not such objects or require some complex operations. In fact, iterative solvers are objects that support any kind of operator on vector classes. The following example illustrates how to use the GMRES solver using an operator class that implements the action of TermMatrix on a vector (here a double product):

// operator class to deal with TermMatrix double product
class myOperator
{
   const TermMatrix *A1_p, *A2_p; //pointers to TermMatrix
   public:
   myOperator(const TermMatrix& A,const TermMatrix& B)
   : A1_p(&A), A2_p(&B) {}
};

void multMatrixVector(const myOperator& A,const TermVector& X,TermVector& R)
{R=(*A1_p)*()(*A2_p)*X);} //product A1∗(A2∗X)
...
//assume TermMatrix A1, A2 built and TermVector B built
myOperator A(A1,A2);
GmresSolver gmres;          // Gmres solver object
TermVector X=gmres(A,B);    // compute solution

 TermVector X=Gmres()(A,B); // compact call

Warning

Be cautious when dealing with large structures. In particular, use pointers or references to avoid unnecessary copy.

If you plan to use other matrix operator/vector classes, you will have to define additional stuff. The operator class, say Mat, must propose the following functions:

ValueType Mat::valueType() // returning type (Real or Complex)
void multMatrixVector(const Mat&,const Vec&,Vec&) // all solvers
void multVectorMatrix(const Vec&,const Mat&,Vec&) // for Bicg and Qmr solvers
// SOR requires also
void Mat::sorLowerMatrixVector(const Vec&,Vec&,Real) const; // [w∗D + L] ∗ x
void Mat::sorUpperMatrixVector(const Vec&,Vec&,Real) const; // [w∗D + U] ∗ x
// SSOR requires also
void Mat::sorDiagonalMatrixVector(const Vec&,Vec&,Real) const;// [w∗D] ∗ x
void Mat::sorLowerSolve(const Vec&,Vec&,Real) const; // [D/w + L] x = b
void Mat::sorUpperSolve(const Vec&,Vec&, Real) const; // [U/w + U] x = b

The TermVector and Vector classes of XLiFE++ may be used in iterative solvers without any additional stuff. However, to deal with any vector class, say Vec, the following functions have to be defined:

Vec::Vec(const Vec&)             // copy constructor
Vec& Vec::operator*=(Real)       // X∗=a
Vec& Vec::operator*=(Complex)    // X/=a
Vec& Vec::operator*=(Complex)    // X∗=a
Vec& Vec::operator*=(Real)       // X/=a
Vec& Vec::operator+=(const Vec&) // X+=Y
Vec& Vec::operator-=(const Vec&) // X−=Y
Real Vec:norm2()                 // |X|2
Complex dotRC(const Vec&, const Vec&);            // X.Y
Complex hermitianProduct(const Vec&, const Vec&); // X|Y = X.conj(Y)

Even if the class is related to real value vector, complex versions are required for compilation reasons but they will not be used!

To use any preconditioning class, say Prec, the minimal requirements are:

Prec::precondMatrix_p // pointer to an object of Mat class
Vec Prec::solver(Vec&) // solution of P∗x = b

Eigen solvers

XLiFE++ currently provides a built-in solver which targets Hermitian and non-Hermitian eigenvalue problems, standard or generalized, and a wrapper to the well known external library Arpack++. The internal solver is provided in case Arpack++ is not available (see How to install Arpack library subsection 1.3) ; as far as possible, the latter should be preferred.

In the following, we will denote the eigen problems: find \((\lambda,x)\) (eigen pair) such that

• \(Ax=\lambda x\), a standard eigenvalue problem,

• \(Ax=\lambda B x\), a generalized eigenvalue problem.

The nature of the problem to be solved is determined by the matrix \(A\): real or complex, symmetric or not, etc. Both solvers can be used in a rather uniform way, although some parameters may be specific to one package or the other. The calling sequence requires a few mandatory arguments ; some optional ones are provided by the user in the form “_key = value”.

Call an eigen solver

Given two suitable TermMatrix objects A and B, a few eigen elements can be computed as the result of one of the generic calling sequence:

EigenElements ees = eigenSolve(A);    // standard eigenvalue problem
EigenElements eeg = eigenSolve(A, B); // generalized eigenvalue problem

The function eigenSolve() automatically selects Arpack++ if it is available, or the internal solver otherwise. Here, \(10\) (the default number) eigen pairs are computed.

Note

The user may choose himself by adding the argument _solver=_intern or _solver=_arpack. Arpack requires the \(RHS\) matrix \(B\) to be hermitian to ensure the convergence of the computation. When this does not seem to be the case, the original generalized problem is automatically transformed into a standard problem.

The user has always direct access and full control over the parameters (which are never modified in this case) by using the specific functions: the function eigenInternSolve provides a direct access to the built-in solver, while arpackSolve uses Arpack. With these functions, the statements in the previous example would become:

// specific call to internal engine
EigenElements eesi = eigenInternSolve(A); // standard eigenvalue problem
EigenElements eegi = eigenInternSolve(A, B); // generalized eigenvalue problem

// specific call to Arpack engine
EigenElements eesa = arpackSolve(A); // standard eigenvalue problem
EigenElements eega = arpackSolve(A, B); // generalized eigenvalue problem

Results

All these functions store their result in an EigenElements object that holds two containers:

• values, containing the list of the found eigenvalues (Complexes).

• vectors, containing the list of the corresponding eigenvectors (TermVectors).

The eigenvectors are always computed together with the eigenvalues. Both containers have the same size which can be obtained with the member function numberOfEigenValues(). For example, the following code prints the computed eigenvalues stored in \(eeg\), the real part and the imaginary part being separated with a white space if they are complex:

if (eeg.isReal())
{ // eigenvalues and eigenvectors are real
  for (int i=1; i <= eeg.numberOfEigenValues(); i++)
  { cout << eeg.value(i).real() << endl; }
}
else
{ // eigenvalues or eigenvectors may not be real
  for (int i=1; i <= eeg.numberOfEigenValues(); i++)
  { cout << eeg.value(i).real() << " " << eeg.value(i).imag() << endl; }
}

The eigenvalues are always returned as complex numbers, even if the problem is real symmetric in which case the imaginary parts are set to 0. The eigenvectors are real if the problem is real symmetric, complex otherwise. By default, the eigenvalues are sorted by increasing module. There are several sorting possibilities which can be specified by the _sort key (see below).

As eigen vector are TermVector objects, they can be saved individually into a file using one of the output format:

saveToFile("V1", eeg.vector(1), _vtk);

Moreover, an EigenElements object can be saved in multiple files in a single statement:

saveToFile("EV", eeg, _vtk);

The names of all the created files will begin with the same prefix given as first argument (here EV) ordering according to the chosen sorting criterion.

Calling sequence

The functions eigenSolve(), eigenInternSolve() and arpackSolve() taking mandatory A, B matrices as first argument may have other arguments managed with some keys.

Optional arguments

• _nev: (integer) number of eigen elements to be computed (default value is 10).

• _which: (string) specifies which part of the spectrum is to be scanned:

  Value	description	solver
  BE	eigenvalues from both ends of the spectrum	arpack
  LA	eigenvalues with largest algebraic value	arpack
  SA	eigenvalues with smallest algebraic value	arpack
  LM	eigenvalues with largest magnitude	arpack and built-in
  SM	eigenvalues with smallest magnitude	arpack and built-in
  LR	eigenvalues with largest real part	arpack
  SR	eigenvalues with smallest real part	arpack
  LI	eigenvalues with largest imaginary part	arpack
  SI	eigenvalues with smallest imaginary part	arpack

• _sigma: (real or complex) shift value \(\sigma\) used in the spectral transformation in order to scan a portion of the spectrum around.

• _mode: (enumeration) following computational modes are implemented:

  • _krylovSchur only for built-in solver : the block Krylov-Schur method (default mode)

  • _Davidson only for built-in solver, suited only for hermitian problems and sometimes faster than the block Krylov-Schur algorithm.

  • _buckling or _cayley mode, only for Arpack solver for a generalized real symmetric problem.

  • _cshiftRe or _cshiftIm for the complex shift invert mode, for a generalized real nonsymmetric problem.

• _ncv: (integer) only for Arpack++ solver, number of Arnoldi vectors to be computed. It must be less than the dimension of the problem. The default value is computed by Arpack.

• _convToStd: no value, only for Arpack++ solver, to force the conversion of a generalized problem into a standard one.

• _forceNonSym: no value, only for Arpack++ solver, to force to use a nonsymmetric computational mode although the problem is symmetric.

• _tolerance: (real) precision of the computation. The default value is 1e-6.

• _maxIt: (integer) maximum number of iterations. The default value is 10000.

• _verbose: (integer) verbosity level. The default value is the value used in the main frame.

• _sort: (enumeration) sort criterion. The default value is _incr_module, which means “by increasing module”. One can also sort by increasing real part (_incr_realpart) and by increasing imaginary part (_incr_imagpart) ; conversely, one can sort by decreasing order by selecting one of _decr_module, _decr_realpart or _decr_imagpart.

Note

It should be noticed that the parameters _nev, _tolerance, _maxIt, _ncv and _verbose can be used in any case. On the contrary, _which and _sigma are mutually exclusive; the latter takes precedence over the former.

The following calls compute the \(20\) eigenvalues of largest magnitude using the block Davidson method and the \(20\) eigenvalues of smallest magnitude using Arpack++:

Number nev = 20;
EigenElements ee = eigenInternSolve(A, B, _nev=nev, _which="LM", _mode=_davidson);
EigenElements ea = arpackSolve(A, _nev=nev, _which="SM", _tolerance=1.e-12);

For a better understanding of all those parameters, see Eigen solvers.

After a computation with Arpack, one can inquire about informations related to this last computation. The simplest way to get these informations is to call the function

String arEigInfos();

which gathers the main informations into a string.

A full example

The following program computes the smallest eigenvalues of the Laplace operator on the segment \([0; \pi]\) with Neumann conditions. The approximation is made with only one finite element with an interpolation degree \(k=60\) and a quadrature rule of degree \(2k+1\). The expected eigenvalues are the square of the integers, i.e. \(0, 1, 4, 9, 16, 25, 36, 49\), etc. Two computational modes are shown. After the call to arpackSolve, information about the computation done is retrieved and printed, as long as the converged eigenvalues and the corresponding eigenvectors.

#include "xlife++.h"
using namespace xlifepp;

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of XLiFE++

  Number nbint=1; // number of intervalls
  Number dk=60;   // interpolation degree
  theCout << "Interpolation degree = " << dk << eol;
  Segment seg(_xmin=0, _xmax=pi_, _nnodes=nbint+1);
  Mesh zeroPi(seg);
  Domain omega = zeroPi.domain("Omega");
  Space Vk(_domain=omega, _FE_type=Lagrange, _FE_subtype=GaussLobattoPoints, _order=dk, _Sobolev_type=H1, _name="Vk");
  Unknown u(Vk, _name="u");   TestFunction v(u, _name="v");
  Number qrodeg = 2*dk+1;
  BilinearForm muv = intg(omega, u * v, _quad=defaultQuadrature, _order=qrodeg),
  auv = intg(omega, grad(u) | grad(v), _quad=defaultQuadrature, _order=qrodeg);
  TermMatrix S(auv, _name="auv"), M(muv, _name="muv");

  // The eigenvalue problem writes S x = l M x
  // Compute the nev first eigenvalues with the smallest magnitude with Arpack
  Number nev = 8;
  EigenElements areigs = arpackSolve(S, M, _nev=nev, _which="SM");
  // Other computational mode choice, here more powerful:
    EigenElements areigs = arpackSolve(S, M, _nev=nev, _sigma=0.5);

  theCout << arEigInfos();
  theCout.precision(17);
  theCout << "Eigenvalues :" << endl;
  Number nconv = areigs.numberOfEigenValues();
  for (Number i = 0; i < nconv; i++) { cout << areigs.value(i+1).real() << endl; }
  saveToFile("Sy", areigs, _format=matlab);
}

The output produced by the SM mode:

Summary of last Arpack computation:
Number of eigenvalues (requested / converged): 8 / 8
Computational mode: regular inverse mode (generalized problem)
Part of the spectrum requested: SM
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 443 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
1.6569854567517169e-10
0.99999999999869593
4.0000000000087512
9.0000000000560245
16.000000000016872
25.000000000006708
36.000000000077279
48.999999999728566

The output produced by using a sigma shift:

Summary of last Arpack computation:
Number of eigenvalues (requested / converged): 8 / 8
Computational mode: shift and invert mode
Shift used: (0.5,0)
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 4 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
9.5701224722688494e-14
0.9999999999997693
4.0000000000003446
8.9999999999997247
15.999999999999394
25.000000000000259
35.999999999999922
48.999999999999908

We can observe that the eigenvalues are numerically close to the previous ones. It’s worth noting that the first one, which is expected to be 0, is better approximated with the shifted computational mode, and the number of iterations is reduced from 443 to 4. The eigenvectors are shown on the following figure:

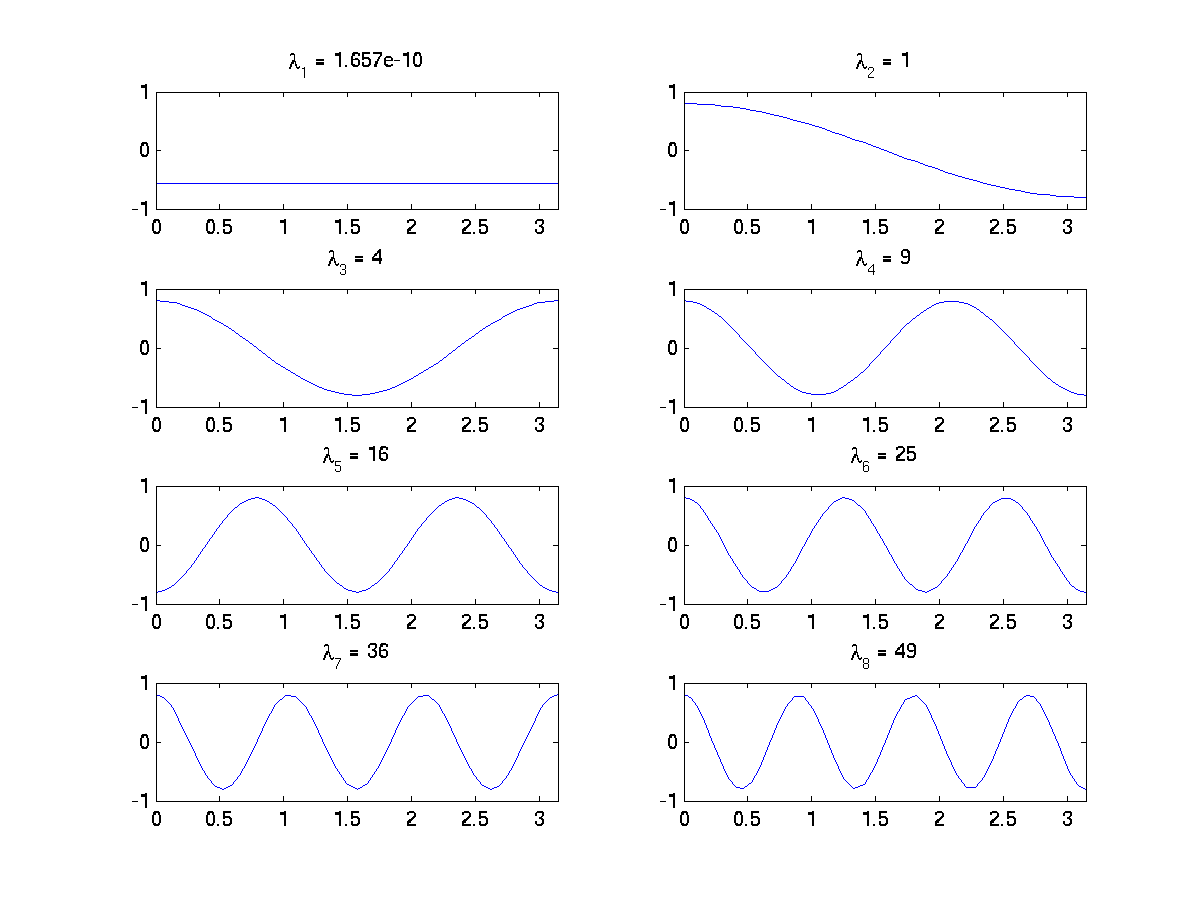
Fig. 55 First eigenvectors of Laplace operator on a segment with Neumann conditions.

Advanced usage of Arpack

When the definition of the operator involves other algebraic operations than the matrix product, like the computation of the inverse of a matrix for example, the above process cannot be used. But it is possible by defining user class providing all operations required by Arpack++ (several products of matrix and vector) to use the Arpack solver:

• create a user class to define the operators of the problem (this requires some programming work),

• use it to create an ArpackProb intermediate object (this is straightforward),

• call arpackSolve with this object as unique argument.

See language reference documentation (Eigen solvers) for details and examples.