Eigen solvers

XLiFE++ currently provides a built-in solver which targets Hermitian and non-Hermitian eigenvalue problems, standard or generalized, and a wrapper to the well known external library Arpack via its companion package Arpack++. The internal solver is provided in case Arpack is not available (see How to install Arpack library subsection 1.3) ; as far as possible, the latter should be preferred.

In the following, we will denote the problems using the generic form:

• \(Ax=\lambda x\), for a standard eigenvalue problem,

• \(Ax=\lambda B x\), for a generalized eigenvalue problem.

The couple \((\lambda,x)\) is called an eigen pair, and consists of an eigenvalue \(\lambda\) and the corresponding eigenvector \(x\). The nature of the problem to be solved is determined by the matrix \(A\): real or complex, symmetric or not, etc.

Both solvers can be used in a rather uniform way, although some parameters may be specific to one package or the other. The calling sequence requires a few mandatory arguments ; some optional ones are provided by the user in the form “_key = value”.

In the following, we describe some features common to both solvers, targeting in particular the result object. Then the parameters governing the computation are described for the built-in solver, followed by those related to Arpack, including a special help paragraph that is worth to be mentioned right now. At last, two special sections are devoted to post-computation information retrieving and an advanced usage of Arpack.

Call an eigen solver

Given two suitable \(TermMatrix\) objects \(A\) and \(B\), corresponding to the mathematical operators \(A\) and \(B\) above, a few eigen elements can be computed as the result of one of the generic calling sequence:

EigenElements ees = eigenSolve(A); // standard eigenvalue problem
EigenElements eeg = eigenSolve(A, B); // generalized eigenvalue problem

In this example, \(10\) (the default number) eigen pairs are computed from the unique knowledge of the mandatory arguments \(A\), or \(A\) and \(B\) ; the other parameters are left to their default values. The function eigenSolve automatically selects Arpack if it is available, or the internal solver otherwise.

Note

The user may choose himself by adding the argument _solver=_intern or _solver=_arpack.

If they are present, the other parameters, given in the form “_key = value”, are checked and passed to the specific solver. Moreover, when Arpack is used, some of them may be modified to benefit from experience feedback. Also, Arpack requires the \(RHS\) matrix \(B\) to be hermitian to ensure the convergence of the computation. When this does not seem to be the case, the original generalized problem is automatically transformed into a standard problem. Whenever such a decision is made or a parameter is modified, an information message is printed on the terminal and in the main print file of XLiFE++.

The user has always direct access and full control over the parameters (which are never modified in this case) by using the specific functions: the function eigenInternSolve provides a direct access to the built-in solver, while arpackSolve uses Arpack. With these functions, the statements in the previous example would become:

// specific call to internal engine
EigenElements eesi = eigenInternSolve(A); // standard eigenvalue problem
EigenElements eegi = eigenInternSolve(A, B); // generalized eigenvalue problem

// specific call to Arpack engine
EigenElements eesa = arpackSolve(A); // standard eigenvalue problem
EigenElements eega = arpackSolve(A, B); // generalized eigenvalue problem

Results

All these functions store their result in an EigenElements object that holds two containers:

• values, containing the list of the found eigenvalues,

• vectors, containing the list of the corresponding eigenvectors.

The eigenvectors are always computed together with the eigenvalues. Both containers have the same size which can be obtained with the member function numberOfEigenValues(). The list values is in fact a vector of complex numbers (even if the problem is real symmetric), and vectors is a vector of TermVector objects. Given an EigenElements object \(eeg\) , these containers can be used directly by \(eeg.values\) and \(eeg.vectors\) with the standard C++ syntax ; alternatively, some member functions are available to extract the eigen pairs using their number, starting at 1. Their names are simply value and vector. For example, the following code prints the computed eigenvalues stored in \(eeg\), the real part and the imaginary part being separated with a white space if they are complex:

if (eeg.isReal())
{ // eigenvalues and eigenvectors are real
  for (int i=1; i <= eeg.numberOfEigenValues(); i++)
  { cout << eeg.value(i).real() << endl; }
}
else
{ // eigenvalues or eigenvectors may not be real
  for (int i=1; i <= eeg.numberOfEigenValues(); i++)
  { cout << eeg.value(i).real() << " " << eeg.value(i).imag() << endl; }
}

The type of the eigenvalues depends on the problem. It can be retrieved by the member function isReal(), as shown above, which returns true if the problem is real symmetric, false otherwise.

The eigenvalues are always returned as complex numbers, even if the problem is real symmetric in which case the imaginary parts are set to 0. The eigenvectors are real if the problem is real symmetric, complex otherwise.

By default, the eigenvalues are sorted by increasing module ; the eigen pairs are internally stored according to this order. There are several sorting possibilities which can be specified by the _sort key (see below).

The eigenvectors can be easily used in the following of the program, since they are available as TermVector objects. They can also be saved individually into a file using one of the output format, in order to be plotted afterwards. The statement:

saveToFile("V1", eeg.vector(1), _vtk);

creates the file V1_Omega.vtk, whose name is build from the prefix given by the user and the name of the domain where the solution is computed ; the suffix is automatically appended according to the output format (here .vtk).

Moreover, an EigenElements object can be saved in multiple files in a single statement:

saveToFile("EV", eeg, _vtk);

The names of all the created files will begin with the same prefix given as first argument (here EV). The eigenvalues will be written in the file EV_eigenvalues and the ith eigenvector will be written in the file EV_i_DomainName.ext, where DomainName will be replaced with the domain name and the extension depend on the chosen format (here .vtk). The eigenvalues are printed in the file EV_eigenvalues from the first one to the last one according to the chosen sorting criterion ; the eigenvectors are printed in files whose numbers follow the same order.

Calling sequence

Let’s recall that the functions eigenSolve, eigenInternSolve and arpackSolve have two main calling sequences according to the kind of problem to define. The arguments can be:

• A, _key1=value1, …_keyN=valueN, in the case of a standard eigenvalue problem,

• A, B, _key1=value1, …_keyN=valueN, in the case of a generalized eigenvalue problem.

The arguments A and B are TermMatrix objects. The others (key, value) pairs are not mandatory. They are used to specify some particular settings. They can be given in any order and their list is given in the corresponding sections below.

Optional parameters for the built-in eigen solver

The built-in eigen solver accepts the following keys:

• _nev: (integer) number of eigen elements to be computed. The default value is 10.

• _which: (string) specifies which part of the spectrum is to be scanned. The default value is “LM”, for largest magnitude. The other possible value is “SM”, for smallest magnitude.

• _sigma: (real or complex) shift value \(\sigma\) used in the spectral transformation in order to scan a portion of the spectrum around.

• _mode: (enumeration), two computational modes are implemented:

  • the block Krylov-Schur method, based on Krylov decomposition with Rayleigh quotient ably reduced to Schur form, and suitable for hermitian and non hermitian eigenvalue problems. To call it, use the value _krylovSchur. This is the default.

  • the block Davidson method, suited only for hermitian problems and sometimes faster than the block Krylov-Schur algorithm. To call it, use the value _davidson.

• _tolerance: (real) precision of the computation. The default value is 1e-6.

• _maxIt: (integer) maximum number of iterations. The default value is 10000.

• _verbose: (integer) verbosity level. The default value is the value used in the main frame.

• _sort: (enumeration) sort criterion. The default value is _incr_module, which means “by increasing module”. One can also sort by increasing real part (_incr_realpart) and by increasing imaginary part (_incr_imagpart) ; conversely, one can sort by decreasing order by selecting one of _decr_module, _decr_realpart or _decr_imagpart.

Examples:

The following call computes the \(20\) eigenvalues of largest magnitude (and the corresponding eigenvectors) of a generalized eigenvalue problem using the block Davidson method:

Number nev = 20;
EigenElements ee = eigenInternSolve(A, B, _nev=nev, _which="LM", _mode=_davidson);

The following call computes \(nev\) eigenvalues around the complex shift value \(2.5+i\) (and the corresponding eigenvectors) of a generalized eigenvalue problem using the block Krylov-Schur method:

Complex sig = (2.5, 1.);
EigenElements ee = eigenInternSolve(A, B, _nev=ne

Optional parameters for Arpack solver

The Arpack solver accepts the following keys:

• _nev: (integer) number of eigen elements to be computed. The default value is 10.

• _which: (string) specifies which part of the spectrum is to be scanned. The default value is “LM”, for largest magnitude. The possible values are:

  Value	description
  BE	eigenvalues from both ends of the spectrum
  LA	eigenvalues with largest algebraic value
  SA	eigenvalues with smallest algebraic value
  LM	eigenvalues with largest magnitude
  SM	eigenvalues with smallest magnitude
  LR	eigenvalues with largest real part
  SR	eigenvalues with smallest real part
  LI	eigenvalues with largest imaginary part
  SI	eigenvalues with smallest imaginary part

For symmetric problems, _which must set to be one of LA, SA, LM, SM or BE. For real nonsymmetric and complex problems, the alternatives are LM, SM, LR, SR, LI and SI.

• _sigma: (real or complex) shift value \(\sigma\) used in the spectral transformation in order to scan a portion of the spectrum around \(\sigma\).

• _mode: (enumeration) when a shift is specified (thanks to _sigma), some additional computational modes are available. In order to activate one of them, one of the following keywords should be specified:

  • _buckling or _cayley for the Buckling mode or the Cayley mode, for a generalized real symmetric problem,

  • _cshiftRe or _cshiftIm for the complex shift invert mode, for a generalized real nonsymmetric problem.

• _tolerance: (real) precision of the computation. The default value is set by Arpack to the machine epsilon.

• _maxIt: (integer) maximum number of iterations. The default value is computed by Arpack.

• _ncv: (integer) number of Arnoldi vectors to be computed. It must be less than the dimension of the problem. The default value is computed by Arpack. WHen eigenSolve is used, this default value is a little improved for small/intermediate linear systems.

• _convToStd: parameter specified to force the conversion of a generalized problem into a standard one. This key does not take any value: it is present or absent (any assigned value is ignored).

• _forceNonSym: parameter specified to force to use a nonsymmetric computational mode although the problem is symmetric. This key does not take any value: it is present or absent (any assigned value is ignored).

• _verbose: (integer) verbosity level. The possible values are 0 or 1, and the default value is 0, which means no output trace.

• _sort: (enumeration) sort criterion. The default value is _incr_module, which means “by increasing module”. One can also sort by increasing real part (_incr_realpart) and by increasing imaginary part (_incr_imagpart) ; conversely, one can sort by decreasing order by selecting one of _decr_module, _decr_realpart or _decr_imagpart.

For a better understanding of all those parameters, one should know that Arpack classifies the eigenvalue problems first as standard or generalized problems, and second according to the matrix A which can be real symmetric, real nonsymmetric or complex. This makes six categories that all own at least two main computational modes called “regular” and “shift and invert”. The “regular” mode is automatically selected if no shift is given. Some additional particular shifted computational modes exist for generalized problems ; this is summarized in the following table:

Kind of problem	Computational mode	Relevant parameters
Standard, real symmetric, nonsymmetric or complex	Regular shift and invert	_which _sigma
generalized real symmetric	Regular shift and invert Buckling Cayley	_which _sigma _sigma, _mode=_buckling _sigma, _mode=_cayley
generalized real nonsymmetric	Regular Real shift and invert Complex shift and invert (Re) Complex shift and invert (Im)	_which _sigma _sigma, _mode=_cshiftRe _sigma, _mode=_cshiftIm
Generalized complex	Regular shift and invert	_which _sigma

Hint

For a generalized eigenvalue problem:

• if A is real, the matrix B is required to be real symmetric positive semi-definite, except in regular mode where it should be real symmetric positive definite. In bukling mode, the real symmetric matrix A is required to be positive semi-definite while B is only required to be real symmetric indefinite.

• if A is complex, the matrix B is required to be hermitian positive semi-definite, except in regular mode, where it should be positive definite. Notice that B may still be real and symmetric.

It should be noticed that the parameters _nev, _tolerance, _maxIt, _ncv and _verbose can be used in any case. On the contrary, _which and _sigma are mutually exclusive ; the latter takes precedence over the former. Moreover, _mode indicates a particular shifted computational mode, and as such is ignored if it is used without _sigma.

For generalized problems, the shifted modes require the computation of \((A-\sigma B)^{-1}x\) (see the table in the section Advanced usage of Arpack below). When \(A\) is real nonsymmetric and \(\sigma\) is complex, \((A-\sigma B)^{-1}x\) is complex, but the internal computation steps of the algorithm are performed in real arithmetic (the vector \(x\) is real). This saves memory requirements and computation time. This is the reason why the user should specify which part of the operator \((A-\sigma B)^{-1}\), real or imaginary, must be taken into account. Both strategies lead to comparable results (see Arpack’s documentation). The parameter _mode should be set to _cshiftRe to select \(\Re \left((A-\sigma B)^{-1} \right)\); it should be set to _cshiftIm to select \(\Im \left( (A-\sigma B)^{-1} \right)\), and in this case obviously, the imaginary part of \(\sigma\) should not be null.

The parameter _convToStd can be used to convert the generalized problem \(A x = \lambda B x\) into the standard one \(B^{-1} A x = \lambda x\). This feature increases the number of computational modes available. This is done internally with the help of a so-called user-class in a way described in the section Advanced usage of Arpack below.

Hint

When the function eigenSolve() is called to solve a generalized problem, tests are performed to check the hypotheses given above. Thus, if it happens that they do not seem to be fulfilled, the conversion into a standard problem is automatically done and an information message is printed.

In the same spirit, _forceNonSym is a switch useful to allow the computational modes of the real nonsymmetric case to be used for a real symmetric problem ; indeed, it may happen that the symmetric algorithms fail, and using the nonsymmetric algorithms can be helpful to obtain a solution. As a last resort, we can also use the complex algorithms, but the entries of the matrix \(A\) should be first converted to complex (to achieve that, see the second example in the section Advanced usage of Arpack below).

Example:

The following call computes the 20 eigenvalues of smallest magnitude (and the corresponding eigenvectors) of a standard eigenvalue problem using the regular mode, with a prescribed tolerance:

Number nev = 20;
EigenElements ee = arpackSolve(A, _nev=nev, _which="SM", _tolerance=1.e-12);

Some hints about the parameters

The convergence of the algorithms highly depends on the data. The ideal situation is when there is no multiplicity and the eigenvalues are well separated, which is rarely the case in practice. Here are some hints to help convergence to occur.

In regular mode, Arpack is better used to search for eigenvalues of largest magnitude (this is why “LM” is the default value of the parameter _which). Thus, as far as possible, the problem should be written to use this mode. It may happen that the eigenvalues of smallest magnitude are hard to compute ; in this case, try using the shifted mode which is generally very powerful.

If there is multiplicity or the eigenvalues are clustered, consider decreasing or on the contrary increasing the number of requested eigenvalues.

The number of iterations is by default computed by Arpack and is generally large enough ; if convergence is not attained, the tolerance (_tolerance) or the number of Armoldi vectors (_ncv) should be modified in priority. By default, Arpack sets the tolerance parameter to the machine epsilon which insures the computation to be performed with the highest possible precision. This represents the relative precision on the computed eigenvalues. It sometimes happens that this stopping criterion is unattainable and the tolerance value should be increased. On the other hand, a too loose value may lead the algorithm to miss some eigenvalues.

The last parameter that can be tuned is the number of Arnoldi vectors generated by the algorithm at each iteration. This parameter can greatly influence the convergence of the algorithm ; it is related with the dimension of the subspaces associated to the eigenvalues. It must be greater than the number of wanted eigenvalues nev and less than the problem dimension n. By default, Arpack sets it to \(min(2*nev + 1, n-1)\). Increasing this value may facilitate the convergence ; on the other hand, this increases the computational time and the memory consumption.

To sum up, here are some actions that can be undertaken to get convergence, listed in the order it is advisable to try them :

• if possible, use a formulation of the eigenvalue problem in order to use the default “LM” computation mode,

• change the number of requested eigenvalues (_nev),

• change the computation mode (_which, _sigma, _mode, _convToStd, _forceNonSym),

• increase the number of Arnoldi vectors (_ncv),

• increase the tolerance (_tolerance), which will lose precision.

Retrieving post-computation informations

After a computation with Arpack, one can inquire about informations related to this last computation. The simplest way to get these informations is to call the function

String arEigInfos();

which gathers the main informations into a string and returns it. This string can then be printed out.

To do that, arEigInfos calls external functions whose names are the names of the true Arpack++ function names prefixed with ar (the true Arpack++ functions are member functions that should be used in conjunction with an Arpack object ; these ones are external functions that can be directly used alone). The available functions are the following:

• bool arParametersDefined(); which returns true if all internal variables were correctly defined, false otherwise.

• int arConvergedEigenvalues(); which returns the number of eigenvalues found. This is the same value as the one provided by the member function numberOfEigenValues() already seen in the Results section above.

• int arGetMaxit(); which returns the maximum number of Arnoldi update iterations allowed.

• int arGetMode(); which returns the computational mode used as described in the following table:

  Value	Mode
  1	regular mode (standard problems)
  2	regular inverse mode (generalized problems)
  3	shift and invert mode. For real nonsymmetric generalized problems, this option can also mean that a complex shift is being used but, in this case the operator is \(\Re \left( (A-\sigma B)^{-1}\right)\)
  4	buckling mode (real symmetric generalized problems) or shift and invert mode with complex shift and the operator is \(\Im \left( (A-\sigma B)^{-1}\right)\) (real nonsymmetric generalized problems)
  5	Cayley mode (real symmetric generalized problems)

• std::string arGetModeStr(); which returns a user friendly string describing the computational mode used. This function does not exist in Arpack and has been written in complement to the previous one which gives a rather raw information.

• int arGetIter(); which returns the number of Arnoldi update iterations actually taken by Arpack to solve the eigenvalue problem.

• int arGetN(); which returns the dimension of the eigenvalue problem.

• int arGetNcv(); which returns the number of Arnoldi vectors generated at each iteration.

• int arGetNev(); which returns the number of required eigenvalues. The number of eigenvalues actually found, however, is given by the function arConvergedEigenvalues.

• std::complex<double> arGetShift(); which returns the shift \(\sigma\) used to define the spectral transformation. This one is a slightly modified version of the original Arpack’s one in that it returns a complex value ; so if the problem is real symmetric, only the real part is relevant. If the problem is being solved in regular mode, this function will return 0.0. To avoid any confusion in this case, the user should call the function arGetMode before this one.

• double arGetShiftImag(); which returns the imaginary part of the shift when the shift and invert mode is being used to solve a real nonsymmetric problem. This value is also returned as the imaginary part of the previous function.

• double arGetTol(); which returns the stopping tolerance used to find the eigenvalues. It corresponds to the relative accuracy of the computed eigenvalues.

• std::string arGetWhich(); which returns the part of the spectrum the user is seeking for. The returned string is one of those used in conjunction with the parameter _which above.

A full example

The following program computes the smallest eigenvalues of the Laplace operator on a segment with Neumann conditions. The approximation is made with the finite element method using a single element, the segment \([0; \pi]\), with an interpolation degree \(k=60\). The quadrature rule has degree \(2k+1\). The expected eigenvalues are the square of the integers, i.e. \(0, 1, 4, 9, 16, 25, 36, 49\), etc. Two computational modes are shown. After the call to arpackSolve, informations about the computation done are retrieved and printed, as long as the converged eigenvalues and the corresponding eigenvectors.

#include "xlife++.h"
using namespace xlifepp;

 int main(int argc, char** argv) {
 init(argc, argv, _lang=en); // mandatory initialization of XLiFE++

 theCout << " Eigenvalues of the 1D Laplace operator with Neumann conditions\n";
 theCout << " ==============================================================\n";

 Number nbint=1; // number of intervalls
 Number dk=60; // interpolation degree
 theCout << "Interpolation degree = " << dk << eol;

 // mesh : segment [0, pi]
 Segment seg(_xmin=0, _xmax=pi_, _nnodes=nbint+1);
 Mesh zeroPi(seg);
 Domain omega = zeroPi.domain("Omega");

 Space Vk(_domain=omega, _FE_type=Lagrange, _FE_subtype=GaussLobattoPoints, _order=dk, _Sobolev_type=H1, _name="Vk");
 Unknown u(Vk, "u");
 TestFunction v(u, "v");

 Number qrodeg = 2*dk+1;
 BilinearForm muv = intg(omega, u * v, defaultQuadrature, qrodeg),
 auv = intg(omega, grad(u) | grad(v), defaultQuadrature, qrodeg);
 // Compute the Stiffness and Mass matrices
 TermMatrix S(auv, "auv"), M(muv, "muv");

 // The eigenvalue problem writes S x = l M x
 // Compute the nev first eigenvalues with smallest magnitude with Arpack
 Number nev = 8;
 EigenElements areigs = arpackSolve(S, M, _nev=nev, _which="SM");
 // Other computational mode choice, here more powerfull:
 // EigenElements areigs = arpackSolve(S, M, _nev=nev, _sigma=0.5);

 theCout << arEigInfos();

 theCout.precision(17);
 theCout << "Eigenvalues :" << endl;
 Number nconv = areigs.numberOfEigenValues();
 for (Number i = 0; i < nconv; i++) { cout << areigs.value(i+1).real() << endl; }

 saveToFile("Sy", areigs, matlab);
 }

The output produced by this program is the following:

Eigenvalues of the 1D Laplace operator with Neumann conditions
==============================================================

Interpolation degree = 60
computing FE term intg_Omega grad(u) | grad(v), using 1 threads : done
computing FE term intg_Omega u * v, using 1 threads : done

Summary of last Arpack computation:
Number of eigenvalues (requested / converged): 8 / 8
Computational mode: regular inverse mode (generalized problem)
Part of the spectrum requested: SM
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 443 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
1.6569854567517169e-10
0.99999999999869593
4.0000000000087512
9.0000000000560245
16.000000000016872
25.000000000006708
36.000000000077279
48.999999999728566

If we comment the line containing the first call to arpackSolve using regular computational mode and uncomment the second one using a shift, the last part of the output is the following:

Summary of last Arpack computation:
Number of eigenvalues (requested / converged): 8 / 8
Computational mode: shift and invert mode
Shift used: (0.5,0)
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 4 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
9.5701224722688494e-14
0.9999999999997693
4.0000000000003446
8.9999999999997247
15.999999999999394
25.000000000000259
35.999999999999922
48.999999999999908

We can observe that the eigenvalues are numerically close to the previous ones. It’s worth noting that the first one, which is expected to be 0, is better approximated with the shifted computational mode, and the number of iterations is reduced from 443 to 4. Indeed, using a shifted mode is often suitable since the convergence is attained faster than with the “SM” mode, but this is not a general rule and this depends on the problem. Moreover, the choice of the shift should be made manually and carefully since every eigenvalue is forbidden. Here, in order to retrieve the eigenvalues of smallest magnitude, the value 0.5 has been chosen, which lies between the first two eigenvalues.

The last statement of the program produces nine files ; their names are Sy_eigenvalues, which contains the eigenvalues, and Sy_i_Omega.m with i equal to 1, 2…8, which contain the components of the eigenvectors, one eigenvector per file. Of course, the two computational modes give the same eigenvectors, possibly with a change in the sign. They are shown on the following figure (obtained as described in section 9.3Graphical exploitation) :

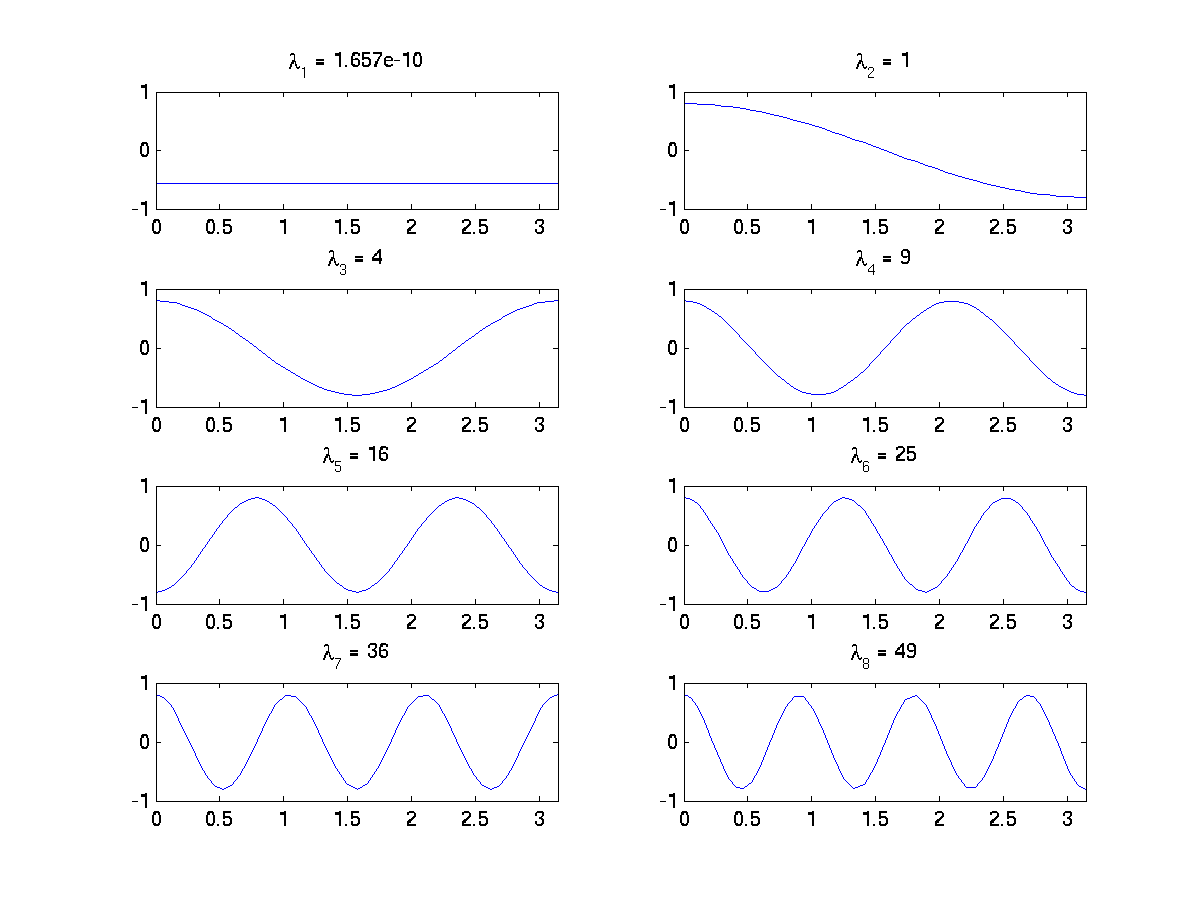
Fig. 151 First eigenvectors of Laplace operator on a segment with Neumann conditions.

Advanced usage of Arpack

The way the function arpackSolve is to be used, as presented so far, is sufficient if the operator A can be expressed as a linear combination of TermMatrix objects, or more frequently as a unique TermMatrix object built from a combination of bilinear forms. However, when the definition of the operator involves other algebraic operations, like the computation of the inverse of a matrix for example, the above process cannot be used.

Indeed, it requires the creation of a specific object containing the sequence of operations needed to define the operator. In other words, the user has to write a class describing the way the operator can be computed.

Hint

This strategy is used internally in XLiFE++ when the function eigenSolve is called to transform a generalized problem into a standard one when the matrix B is not hermitian.

General guidelines

In order to get rid of the technicalities of Arpack++ and to help to the creation of the user class, a general frame has been prepared that involves the creation of an intermediate placeholder object whose type is ArpackProb, designed to hold the characteristics of the true Arpack++ object internally created. The definition of the user class should be made in coherence with the Arpack computational mode chosen, hold in the ArpackProb object. To summarize this, the user has to:

• create a so-called user class to define the operators of the problem (this requires some programming work),

• use it to create an ArpackProb intermediate object (this is straightforward),

• call arpackSolve with this object as unique argument.

Arpack++’s usage made here imposes the user class to define some matrix-vector products related to the computational mode chosen. The required products are described in the documentation of Arpack++ and are summarized in the following table. The name of the member functions, MultOPx, MultBx and MultAx, are the generic names used in the documentation of Arpack++. They have been kept here to make things easier and should be left unchanged in our context:

Kind of problem	Computational mode	Matrix-vector products	member fcts to use
Standard:
all	Regular	\(y \leftarrow Ax\)	MultOPx
	Shift and invert	\(y \leftarrow (A-\sigma Id)^{-1} x\)	MultOPx
Generalized:
real symmetric	Regular	\(y \leftarrow B^{-1}Ax; x \leftarrow Ax\)	MultOPx
		\(y \leftarrow Bx\)	MultBx
	Shift and invert	\(y \leftarrow (A-\sigma B)^{-1} x\)	MultOPx
		\(y \leftarrow Bx\)	MultBx
	Buckling	\(y \leftarrow (A-\sigma B)^{-1} x\)	MultOPx
		\(y \leftarrow Ax\)	MultBx
	Cayley	\(y \leftarrow (A-\sigma B)^{-1} x\)	MultOPx
		\(y \leftarrow Ax\)	MultAx
		\(y \leftarrow Bx\)	MultBx
real nonsymmetric	Regular	\(y \leftarrow B^{-1}Ax; x \leftarrow Ax\)	MultOPx
		\(y \leftarrow Bx\)	MultBx
	Real shift and invert	\(y \leftarrow (A-\sigma B)^{-1} x\)	MultOPx
		\(y \leftarrow Bx\)	MultBx
	Complex shift and invert (real part)	\(y \leftarrow \Re \left( (A-\sigma B)^{-1} \right) x\)	MultOPx
		\(y \leftarrow Ax\)	MultAx
		\(y \leftarrow Bx\)	MultBx
	Complex shift and invert (imag part)	\(y \leftarrow \Im \left( (A-\sigma B)^{-1} \right) x\)	MultOPx
		\(y \leftarrow Ax\)	MultAx
		\(y \leftarrow Bx\)	MultBx
complex	Regular	\(y \leftarrow B^{-1}Ax; x \leftarrow Ax\)	MultOPx
		\(y \leftarrow Bx\)	MultBx
	Real shift and invert	\(y \leftarrow (A-\sigma B)^{-1} x\)	MultOPx
		\(y \leftarrow Bx\)	MultBx

In order to help to the definition of the user class, we have found convenient to create it as a derived class of ARStdFrame<Real>, ARStdFrame<Complex>, ARGenFrame<Real> or ARGenFrame<Complex>, depending on the nature of the problem, standard or generalized, and its type, real or complex. As their name suggests, these classes are frames prepared to facilitate the definition of the matrix-vector product(s) required by the computational mode chosen. They are abstract classes that declare the matrix-vector products MultOPx, MultBx and MultAx as virtual functions that the user must provide. They have a unique construct or whose prototype is:

template<class K_> ARStdFrame(const TermMatrix& charMat);
template<class K_> ARGenFrame(const TermMatrix& charMat);

The unique argument is a so-called characteristic matrix that allows to retrieve informations about the context of the problem such as its dimension and the associated unknowns. In practice, it is one of the matrices involved in the definition of the operator A. Those two classes derive themselves from the class ARInterfaceFrame that provides, in addition, the member function

int GetN();

which returns the dimension of the problem to be solved.

We will now show how all this takes place and give further details on an example.

User class example 1

We consider again the problem of the Laplace operator on a segment with Neumann conditions (see the previous section). This problem is written and solved there as a generalized eigenvalue problem \(Sx=\lambda Mx\). Now, assume we want to write this problem as a standard eigenvalue problem \(M^{−1}Sx=\lambda x\), which is correct since the mass matrix \(M\) is invertible. We are facing to the operator \(A=M^{−1}S\) that cannot be handled in the framework presented in the previous sections. Thus, we write a special class StdNonSym whose definition is the following:

 class StdNonSym: public ARStdFrame<Real> {
 public:
 //! constructor
 StdNonSym(TermMatrix& S, TermMatrix& M);
 //! destructor
 ~StdNonSym(){ delete fact_p; }

 //! matrix−vector product required : y <− inv(M)∗S ∗ x
 void MultOPx(Real *x, Real *y);

 private:
 //! pointers to internal data objects
 const LargeMatrix<Real> *matS_p, *matM_p;
 //! pointer to temporary factorized matrix M
 LargeMatrix<Real>* fact_p;
}; // end of Class StdNonSym =========================================

This class contains three member functions: a constructor (with two arguments which are the two matrices needed to define the problem), the destructor and the matrix-vector product required, whose name is MultOPx, as mentionned in the previous table.

Since we plan to use the regular computational mode, the function MultOPx should compute the result \(y\) of \(M^{−1}Sx\) for a given \(x\). This is done in two steps: first compute \(z=Sx\), second solve \(My=z\) using a Cholesky factorization of \(M\) which is symmetric positive definite. The function MultOPx may be called many times during the computation, so the Cholesky factorization of \(M\) has to be computed once and stored. This is done in the constructor through the initialization of the pointer fact_p, along with the initialization of the two other pointers matS_p and matM_p (see below). The destructor’s unique role is to free the memory allocated to store the Cholesky factorization. Let’s now describe the constructor and the matrix-vector product in more details. The implementation is the following:

//!
// Assumptions (not checked) :
// S real
// M real symmetric positive definite
StdNonSym::StdNonSym(TermMatrix& S, TermMatrix& M)
: ARStdFrame(S), matS_p(&S.matrixData()->getLargeMatrix<Real>()),
matM_p(&M.matrixData()->getLargeMatrix<Real>()) {
fact_p = newSkyline(matM_p);
ldltFactorize(*fact_p);
}
//! Matrix−vector product y <− inv(M)∗S ∗ x
void StdNonSym::MultOPx(Real *x, Real *y) {
array2Vector(x, lx);
std::vector<Real> Sx(GetN());
multMatrixVector(*matS_p, lx, Sx);
// Solve linear system. Matlab equivalent: ly = matM_p \ Sx;
(fact_p->ldltSolve)(Sx, ly); // store the solution into ly
vector2Array(ly, y);
}

Since StdNonSym derives from ARStdFrame, the ARStdFrame constructor is first called, passing S as the characteristic matrix, and the pointers matS_p and matM_p are initialized. They hold the addresses of the low level LargeMatrix objects containing the effective real data values. The reason is that the algebraic operations are attached to the LargeMatrix class with the adequate storage type. Then the Cholesky factorization of \(M\) is computed in two steps: first record in the pointer fact_p the result of newSkyline, i.e. the address of a copy of the matrix \(M\) stored in skyline storage type, second call the function ldltFactorize to compute the Cholesky factorization.

The prototype of the function MultOPx is imposed by Arpack. Each of the two arguments is the address of a C-style array. But the algebraic operations provided by XLiFE++ require operands whose type are std::vector. Thus, the data values should be copied in and out using the two utilitary functions array2Vector and vector2Array. The two vectors lx and ly are local buffers with the right size prepared for this purpose ; they are members of ARInterfaceFrame and are ready to use. Thus, the input array x is first copied into the local vector lx, then the matrix-vector product Sx is computed by the function multMatrixVector and stored into the local vector Sx. Then comes the resolution of the linear system \(My=Sx\) by the function ldltSolve which uses the precomputed Cholesky factorization through the pointer fact_p. At last, the result is copied from the local vector ly into the output array y.

The following action is to use this user class to create an ArpackProb intermediate object which will set the computational mode to be used by Arpack. For this purpose, five constructors are available. In their list of arguments, usrcl denotes the user class, which bears the the kind of problem to be solved, standard or generalized, and nev is the number of desired eigenvalues:

• Constructors for regular mode (for standard or generalized eigenvalue problems)

  The argument which defines the part of the spectrum to be scanned. The possible values are described in a previous section (see optional parameter _which).

  • real case

    ArpackProb(const ARInterfaceFrame<Real>& usrcl, int nev, const char* which, bool sym = true);
    

  • complex case

    ArpackProb(const ARInterfaceFrame<Complex>& usrcl, int nev, const char* which);
    

    The last argument sym specifies by default to use the algorithm designed for a symmetric operator ; if it takes the value false, then the algorithm designed for a nonsymmetric operator will be used.

• Constructors for shifted computational mode (for standard or generalized problems)

  1. • real symmetric case:

       • for standard problems: shift and invert mode (default)

       • for generalized problems: shift and invert mode (default), Buckling and Caley mode

     • real nonsymmetric case:

       • for standard or generalized problems: (real) shift and invert mode

         ArpackProb(const ARInterfaceFrame<Complex>& usrcl, int nev, const char* which);
         

         As above, the argument sym tells if the algorithm designed for the symmetric case (true) or nonsymmetric case (false) should be used. The argument sigma is the value of the shift (real number here). The buckling and Cayley modes can be selected by giving the argument cMode the character value ’B’ or ’C’ respectively.

         Tip

         for standard eigenvalue problems, this last argument (computational mode cMode ) is irrelevant and thus has not to be specified.

  2. real nonsymmetric case, for generalized problems only: complex shift and invert mode

     ArpackProb(const ARInterfaceFrame<Real>& usrcl, int nev, double sigmaR, double sigmaI, char cMode = 'R');
     

     The shift is given by both its real part, sigmaR, and its imaginary part, sigmaI. The argument cMode should be set to ’R’ to select \(\Re ( (A-\sigma B)^{-1})\) ; it should be set to ’I’ to select \(\Im ( (A-\sigma B)^{-1})\) (for more explanations, see the description of the parameter _mode in the previous section).

  3. complex case, for standard or generalized problems: shift and invert mode

     ArpackProb(const ARInterfaceFrame<Complex>& usrcl, int nev, double sigmaR, double sigmaI = 0.0);
     

     The shift is given by both its real part, sigmaR, and its imaginary part, sigmaI.

In order to terminate this illustration, the last thing to do is to call the solver. Technically, we can reuse the program shown at the end of the previous section and called A full example. and do the following:

1. copy the declaration of the user class StdNonSym, followed by its implementation as given above, just before the main function,

2. replace the call to arpackSolve():

   EigenElements areigs = arpackSolve(S,M, _nev=nev, _which="SM");
   

   by the three lines:

   StdNonSym usrcl(S,M);
   ArpackProb Arpb(usrcl,nev,"SM",false); // false means "use the nonsymmetric algorithm"
   EigenElements areigs = arpackSolve(Arpb);
   

   The first line creates an object called usrcl by calling the constructor of the user class to which the stiffness and mass matrices are passed. Then, the intermediate object Arpb is created using the first constructor in the list just above. This completely defines the Arpack problem: the user class derives from ARStdFrame, so it is a real standard problem ; the eigenvalues of smallest magnitude are requested and the nonsymmetric algorithm is chosen. Indeed, the operator \(A=M^{−1}S\) is not symmetric, so we should select the corresponding computational mode (this justifies the name given to the user class).

3. print the eigenvalues as complex numbers by removing the call to real() in the last line of the program:

   for (int i = 0; i < nconv; i++) { cout << areigs.value(i+1) << endl; }
   

The output produced by this new program is the following:

Interpolation degree = 60
computing FE term intg_Omega grad(u) | grad(v), using 1 threads : done
computing FE term intg_Omega u * v, using 1 threads : done

Number of eigenvalues (requested / converged): 8 / 8
Computational mode: regular mode (standard problem)
Part of the spectrum requested: SM
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 266 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
(-3.9936942641816131e-12,0)
(0.99999999998896483,0)
(3.9999999999884972,0)
(8.9999999999974278,0)
(15.999999999996687,0)
(25.000000000000899,0)
(35.999999999997002,0)
(63.999999992827938,0)

We can observe that the last eigenvalue is close to 64 instead of 49 which has been missed. Inserting the line

Arpb.ChangeTol(1.e-15);

between the declaration of Arpb and the call to arpackSolve sets a slightly relaxed value of the tolerance that suffices to obtain the expected result:

Interpolation degree = 60
computing FE term intg_Omega grad(u) | grad(v), using 1 threads : done
computing FE term intg_Omega u * v, using 1 threads : done

Number of eigenvalues (requested / converged): 8 / 8
Computational mode: regular mode (standard problem)
Part of the spectrum requested: SM
Problem size = 61, Tolerance = 1e-15
Nb_iter / Nb_iter_Max = 252 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
(-3.9815928332131989e-12,0)
(0.99999999998896794,0)
(3.9999999999885101,0)
(8.9999999999974225,0)
(15.999999999996653,0)
(25.000000000000909,0)
(35.999999999996525,0)
(48.999999999971514,0)

Other tuning functions

This gives the opportunity to mention that the parameters governing the computation can be set using exactly the same function names as the ones defined in Arpack++. Besides the function ChangeTol() just seen, we can use the following functions:

• \(ChangeMaxit(int)\) to change the maximum number of iterations,

• \(ChangeNcv(int)\) to change the number of Arnoldi vectors to be computed.

• \(Trace()\) to activate the output of statistics related to the computation.

For more information, see the description of the parameters _maxIt, _ncv and _verbose in the previous section.

User class example 2

As a second example, we can use the complex algorithm to solve the same problem. The operator \(A=M^{−1}S\) should be complex ; for this, we choose to convert the matrix \(S\) to complex. The corresponding user class StdComp is a slight modification of the class StdNonSym:

 class StdComp: public ARStdFrame<Complex> {
 public:
 //! constructor
 StdComp(TermMatrix& S, TermMatrix& M);

 //! destructor
 ~StdComp(){ delete fact_p; }

 //! matrix−vector product required : y <− inv(M)∗S ∗ x
 void MultOPx(Complex *x, Complex *y);

 private:
 //! pointers to internal data objects
 const LargeMatrix<Complex> *matS_p;
 const LargeMatrix<Real> *matM_p;
 //! pointer to temporary factorized matrix M
 LargeMatrix<Real>* fact_p;
}; // end of Class StdComp =========================================

The modifications concern the type of \(S\) and the operands x and y changed to complex. The implementation is thus quite similar to the StdNonSym one:

//!
// Assumptions (not checked) :
// S complex
// M real symmetric positive definite
StdComp::StdComp(TermMatrix& S, TermMatrix& M)
: ARStdFrame(S), matS_p(&S.matrixData()->getLargeMatrix<Complex>()),
matM_p(&M.matrixData()->getLargeMatrix<Real>()) {
       fact_p = newSkyline(matM_p);
      ldltFactorize(*fact_p);
      }
//! Matrix−vector product y <− inv(M)∗S ∗ x
void StdComp::MultOPx(Complex *x, Complex *y) {
    array2Vector(x, lx);
    std::vector<Complex> Sx(GetN());
    multMatrixVector(*matS_p, lx, Sx);
    // Solve linear system. Matlab equivalent: ly = matM_p \ Sx;
    (fact_p->ldltSolve)(Sx, ly); // store the solution into ly
    vector2Array(ly, y);
}

One can just mention the initialization of the pointer matS_p to the complex data values. The factorization of \(M\) is unchanged and it should be noticed that here the Cholesky solver handles complex data.

The final step consists in modifying the initial program (A full example. above) by inserting the declaration and the implementation of the user class StdComp as given above before the main function, and replace the call to arpackSolve() by the three lines:

TermMatrix Sc = toComplex(S);
StdComp usrcl(Sc,M);
ArpackProb Arpb(usrcl,nev,"SM");

The first statement converts the matrix \(S\) to the complex one Sc. Then the object corresponding to the user class usrcl is created from the complex stiffness matrix and the real mass matrix. The intermediate object Arpb is created using the second constructor in the list given above. This completely defines the Arpack problem: the user class derives from ARStdFrame, so it is a complex standard problem ; the eigenvalues of smallest magnitude are requested. All the other parameters are the default ones.

The output produced by this last program is the following:

 Interpolation degree = 60
 computing FE term intg_Omega grad(u) | grad(v), using 1 threads : done
 computing FE term intg_Omega u * v, using 1 threads : done

Number of eigenvalues (requested / converged): 8 / 8
Computational mode: regular mode (standard problem)
Part of the spectrum requested: SM
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 235 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
(1.6895427007126359e-10,-5.3921458890663075e-11)
(1.0000000000208538,-1.1338949016552641e-13)
(4.0000000000304183,7.7808203477527148e-12)
(9.0000000000377973,1.1273274779629001e-11)
(16.000000000012292,2.7943890983902115e-11)
(24.999999999985345,1.3070479010254708e-11)
(36.00000000008869,-3.2309836334379703e-11)
(49.000000000591157,-2.8194647537903334e-10)

User class example 3

At last, we can create a user class defining a generalized problem, what we were starting from and thus redoing in fact what is already done internally when the first calling sequence of the function arpackSolve() presented in the previous section is used. The corresponding user class GenSym is the following :

class GenSym: public ARGenFrame<Real> {
public:
//! constructor
GenSym(TermMatrix& S, TermMatrix& M);

//! destructor
~GenSym(){ delete fact_p; }

//! matrix−vector products required : y <− inv(M)∗S ∗ x and x <− S ∗ x
void MultOPx(Real *x, Real *y);
//! matrix−vector product y <− M ∗ x
void MultBx(Real *x, Real *y);

private:
//! pointers to internal data objects
const LargeMatrix<Real> *matS_p, *matM_p;
//! pointer to temporary factorized matrix M
LargeMatrix<Real>* fact_p;
}; // end of Class GenSym =========================================

Take notice that this class derives from ARGenFrame and in accordance with Arpack’s requirements for a real symmetric generalized problem (see the table above), this class provides the two matrix-vector products MultOPx and MultBx. The implementation is very similar to the StdNonSym’s one:

//!
// Assumptions (not checked) :
// S real symmetric
// M real symmetric positive definite
GenSym::GenSym(TermMatrix& S, TermMatrix& M)
: ARGenFrame(S), matS_p(&S.matrixData()->getLargeMatrix<Real>()),
matM_p(&M.matrixData()->getLargeMatrix<Real>()) {

  fact_p = newSkyline(matM_p);
  ldltFactorize(*fact_p);
}
//! Matrix−vector products y <− inv(M)∗S ∗ x and x <− S ∗ x
void GenSym::MultOPx(Real *x, Real *y) {
  array2Vector(x, lx);
 std::vector<Real> Sx(GetN());
 multMatrixVector(*matS_p, lx, Sx);
 vector2Array(Sx, x);
 // Solve linear system. Matlab equivalent: ly = matM_p \ Sx;
 (fact_p->ldltSolve)(Sx, ly); // store the solution into ly
 vector2Array(ly, y);
}
//! Matrix−vector product y <− M ∗ x
void GenSym::MultBx(Real *x, Real *y) {
 array2Vector(x, lx);
 multMatrixVector(*matM_p, lx, ly);
 vector2Array(ly, y);
 }

The constructor’s code is nearly identical to the one of StdNonSym. The function MultOPxcomputes() the same product \(M^{-1} S\); it additionally stores \(Sx\) in \(x\) which is here both an input and an output argument as required by Arpack. The function MultBx() simply computes the product \(Mx\).

Again, the initial program (A full example above) can be modified by inserting the declaration and the implementation of the user class GenSym before the main function and replace the call to arpackSolve() by:

GenSym usrcl(S, M);
ArpackProb Arpb(usrcl, nev, "SM");
EigenElements areigs = arpackSolve(Arpb);

The first line creates an object called usrcl by calling the constructor of the user class to which the stiffness and mass matrices are passed. Then, the intermediate object Arpb is created using the first of the constructors of the class ArpackProb given above. This completely defines the Arpack problem: the user class derives from ARGenFrame<Real>, so it is a real generalized problem ; the eigenvalues of the smallest magnitude are requested, and the symmetric algorithm is chosen (since this is the default).

The output produced by this new program is the following:

 Interpolation degree = 60
 computing FE term intg_Omega grad(u) | grad(v), using 1 threads : done
 computing FE term intg_Omega u * v, using 1 threads : done

Number of eigenvalues (requested / converged): 8 / 8
Computational mode: regular inverse mode (generalized problem)
Part of the spectrum requested: SM
Problem size = 61, Tolerance = 1.11022e-16
Nb_iter / Nb_iter_Max = 443 / 800, Number of Arnoldi vectors = 17
Eigenvalues :
 1.6569854567517169e-10
 0.99999999999869593
 4.0000000000087512
 9.0000000000560245
 16.000000000016872
 25.000000000006708
 36.000000000077279
 48.999999999728566