`ParametrizedSurface`#

A ParametrizedSurface geometry is defined by a Parametrization object handling a map \((u,v)\in \hat{\Omega}\rightarrow P(u,v)\in \mathbb{R}^3\). In most of the cases, \(\hat{\Omega}=[x_1,x_2]\times[y_1,y_2]\). Since mesh tools, generally, does not support this type of geometry representation, two additional data must be provided, to describe how to partition the surface into small representable pieces:

the type of partition : linear or spline (key _partitioning with value _linearPartition or _splinePartition)
the number of pieces in the partition (key _nbParts )

The following example shows the construction of a ParametrizedSurface using a parametrization defined by a symbolic function and a linear partition with 50 pieces:

Parametrization pars(0,2*pi_,0.,2*pi_, x_1, x_2, cos(x_1)*cos(x_2), Parameters());
ParametrizedSurface Psl(_parametrization = pars, _partitioning=_linearPartition,
                  _nbParts=50, _hsteps=0.2, _domain_name=sh,_side_names="Gamma");

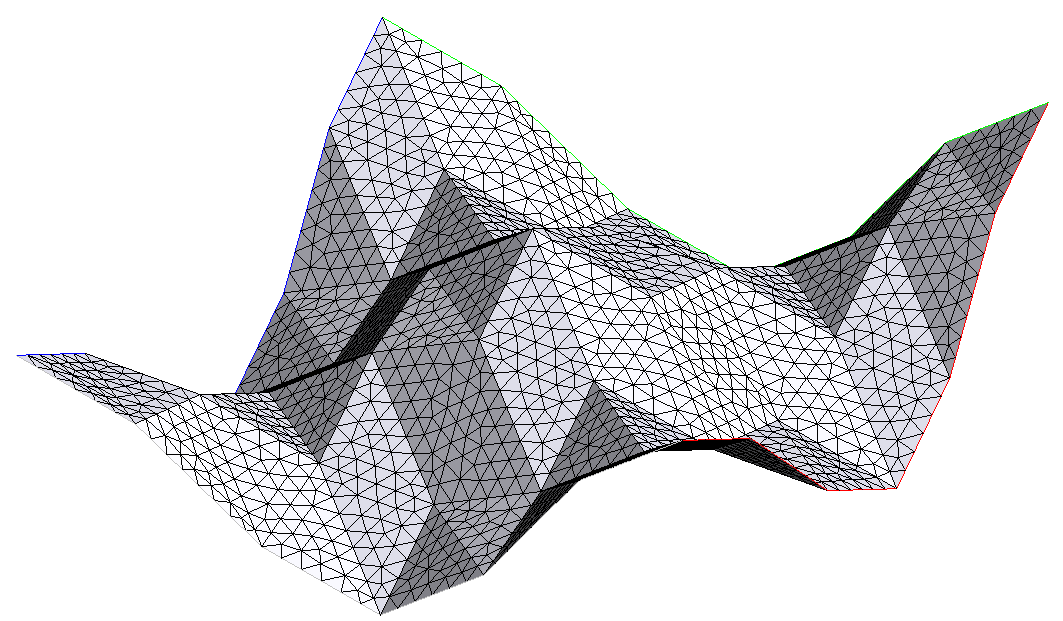
The number of parts (triangles) is not strictly equal to 50 because the partitioning process consists in splitting the u-direction and v-direction relatively to their lengths such the total number of triangles be close to 50. The parameter _hsteps is propagated on all vertices of the triangle partition. It is not yet possible to manage different _hsteps. The side names are numbered relatively to the parametrization: \(v=v_{min}\), \(u=u_{max}\), \(v=v_{max}\), \(u=u_{min}\).

To get a good linear approximation of an oscillating surface, a lot of triangles are required, up to the desired mesh ideally! This is why using a spline partition is a better solution:

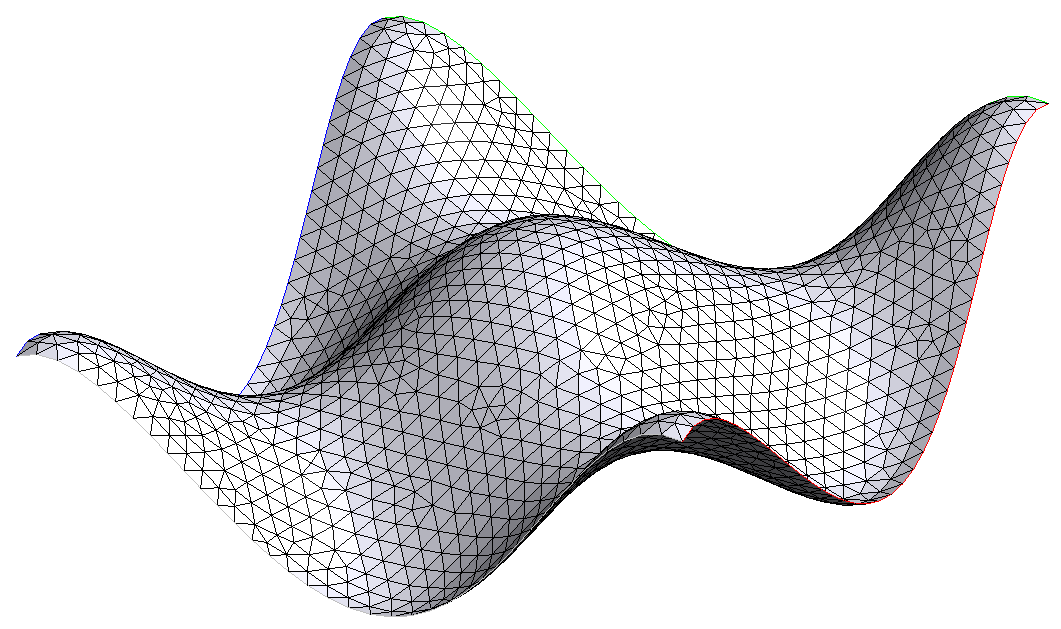
ParametrizedSurface Pss(_parametrization = pars, _partitioning=_splinePartition,
                  _nbParts=16, _hsteps=0.2, _domain_name=sh, _side_names="Gamma");

In addition to the standard keys (_hsteps, _domain_name, …) only the following keys are available:

key(s)	authorized types	examples
`_parametrization`	`Parametrization` object	`_parametrization =pars`
`_partitioning`	_linearPartition , _splinePartition	`_partitioning = _splinePartition`
`_nbParts`	unsigned int (`Number`)	`_nbParts =16`

.

Warning

Be cautious, in any case the surface meshed is an approximated surface of the parametrized surface. As spline partition uses interpolation splines, the approximation may be a quite good one.

Danger

Up to now, the ParametrizedSurface geometry can be meshed only with the OpenCASCADE engine!

ParametrizedSurface#

`ParametrizedSurface`#