Finite elements#

The finiteElements library concerns all the stuff related to the elementary objects of a finite elements discretization, say reference elements that are managed by the base class: RefElement. This class handles the following data:

an Interpolation object carrying some general informations on the finite element such that the finite element type and its conforming space,
a GeomRefElement object describing the geometric support of the element,
a vector of RefDof to handle all the degrees of freedom (DOF) attached to the reference element,
and additionnal stuff useful for the computation (for instance ShapeValues object to store the values of shape functions).

Figure made with TikZ

All concrete finite element classes are organized according to their geometry: LagrangeSegment, LagrangeTriangle, LagrangeTetrahedron, … inherit from the RefElement class through the intermediate classes: RefSegment, RefTriangle, RefTetrahedron, … GeomRefElement also provides child classes: GeomRefSegment, GeomRefTriangle, GeomRefTetrahedron, …

A GeomElement object (geometric element from the mesh) and RefElement are the main components of the Element object, defining a finite element in the physical space. In few words, a Mesh is a collection of GeomElement objects and Space will be a collection of Element objects.

Important

The Space is the user class managing the finite elements parameters at its construction. Other classes are internal classes that handle a lot of information and functionnality.

On segment#

The RefSegment class has three main child classes :

LagrangeStdSegment which implements standard Lagrange element at any order
LagrangeGLSegment which implements Lagrange element based on Gauss-Lobatto points at any order
HermiteStdSegment which implements standard Hermite element, currently only P3 Hermite

Figure made with TikZ

On triangle#

The RefTriangle class provides the following types of element:

standard Lagrange element at any order LagrangeStdTriangle and LagrangeStdTrianglePk; the template LagrangeStdTriangle class is defined only for low order (up to 6) with better performance and LagrangeStdTrianglePk class is designed for any order. It uses a general representation of shape functions on xy-monoms basis get from the solving of a linear system. This method is not stable for very high order.
HermiteStdTriangle which implements standard Hermite element, currently only P3 Hermite (not H2 conforming)
CrouzeixRaviartStdTriangle which implements the Crouzeix-Raviart element, currently only P1 (not H1 conforming)
RaviartThomasTriangle which implements the Raviart-Thomas elements (Hdiv conforming): :cpp:class:` RaviartThomasStdTriangleP1` for Raviart-Thomas standard P1 element and RaviartThomasStdTrianglePk for Raviart-Thomas at any order.
NedelecTriangle which implements the Nedelec elements (Hcurl conforming): NedelecFirstTriangleP1 for Nedelec first family of order 1 element, NedelecFirstTrianglePk for Nedelec first family of any order and NedelecSecondTrianglePk for Nedelec second family of any order.
MorleyTriangle and ArgyrisTriangle elements designed for H2-approximation (non H2 conforming and H2 conforming).

Figure made with TikZ

Lagrange elements#

Fig. 105 Triangle P1 Fig. 106 Triangle P1	Fig. 107 Triangle P2 Fig. 108 Triangle P2
Fig. 109 Triangle P3 Fig. 110 Triangle P3	Fig. 111 Triangle P4 Fig. 112 Triangle P4
Fig. 113 Triangle P5 Fig. 114 Triangle P5	Fig. 115 Triangle P6 Fig. 116 Triangle P6

Raviart-Thomas elements#

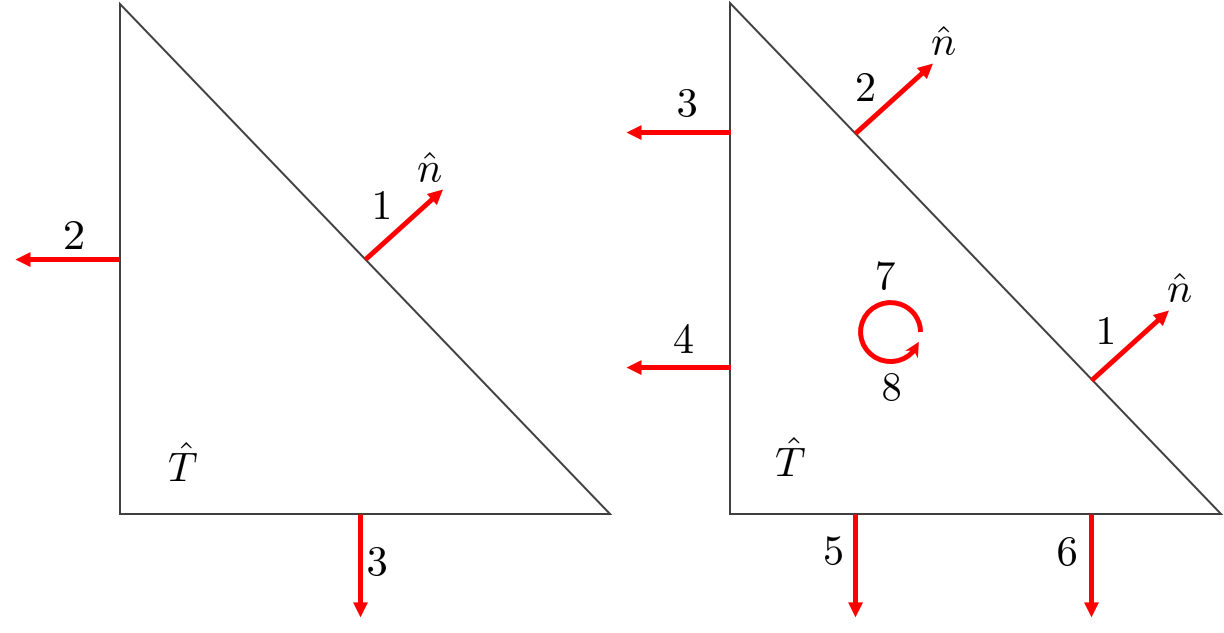
../../_images/RT1_RT2.png — Fig. 117 Raviart-Thomas elements (order 1 and 2)#

Nedelec edge elements#

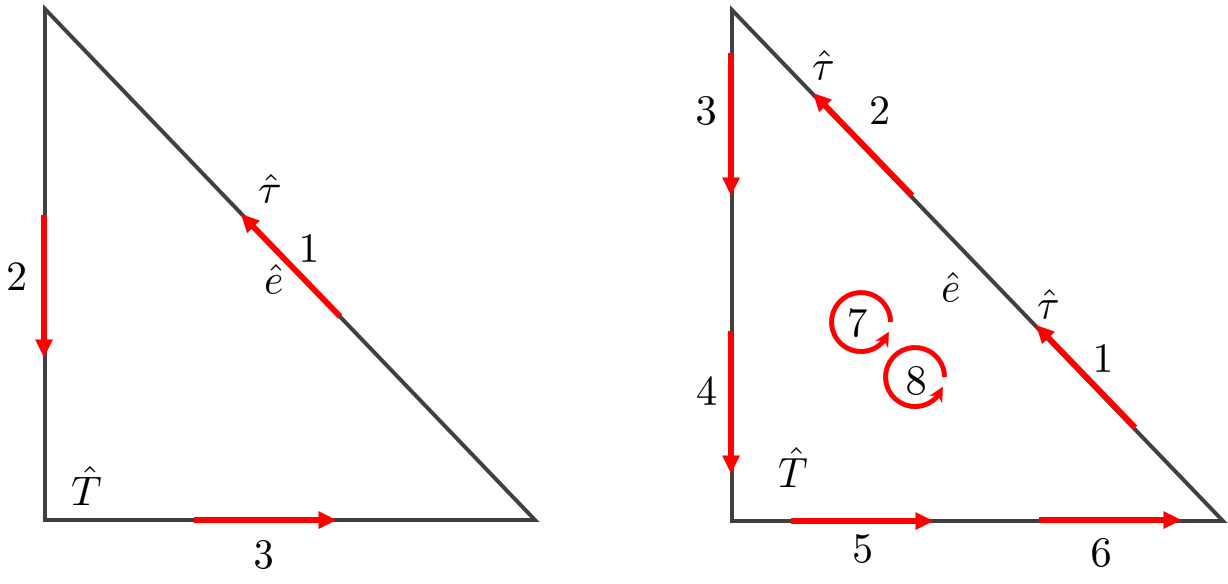
../../_images/NET1_NET2.png — Fig. 118 Nedelec edge elements (order 1 and 2)#

On quadrangle#

The RefQuadrangle class provides

standard Qk-Lagrange element at any order LagrangeStdQuadrangle and LagrangeGLQuadrangle classes inherited from LagrangeStdQuadrangle
the first family Pk-Nedelec element at any order NedelecEdgeFirstQuadranglePk class inherited from NedelecEdgeQuadrangle

Figure made with TikZ

Lagrange elements#

Fig. 119 Quadrangle Q1 Fig. 120 Quadrangle Q1	Fig. 121 Quadrangle Q2 Fig. 122 Quadrangle Q2
Fig. 123 Quadrangle Q3 Fig. 124 Quadrangle Q3	Fig. 125 Quadrangle Q4 Fig. 126 Quadrangle Q4
Fig. 127 Quadrangle Q5 Fig. 128 Quadrangle Q5	Fig. 129 Quadrangle Q6 Fig. 130 Quadrangle Q6

Nedelec edge elements#

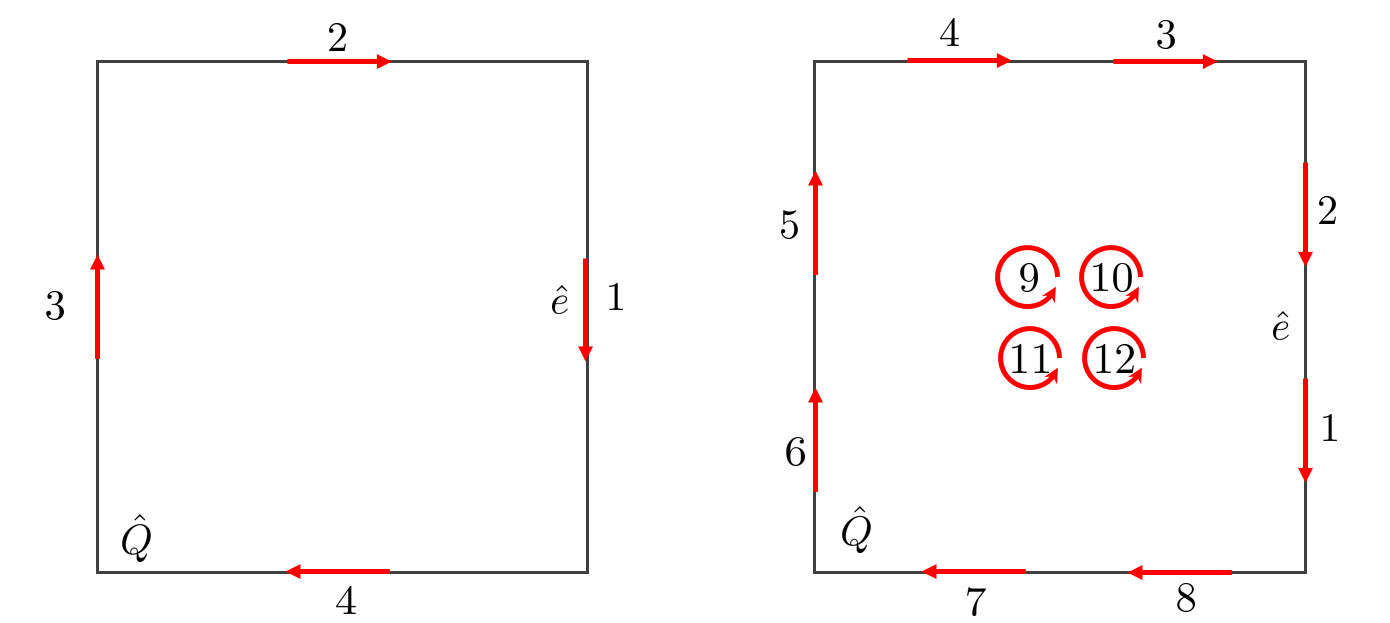
../../_images/NEC1_NEC2.png — Fig. 131 Nedelec edge elements (order 1 and 2)#

On tetrahedron#

Figure made with TikZ

The RefTetrahedron class provides the following types of element:

LagrangeStdTetrahedron class is defined only for low order (up to 6) with better performance and LagrangeStdTetrahedronPk class is designed for any order. It uses a general representation of shape functions on xyz-monoms basis get from the solving of a linear system. This method is not stable for very high order.
CrouzeixRaviartTetrahedron which implements the Crouzeix-Raviart element, currently only P1 (not H1 conforming)
NedelecFaceTetrahedron which implements the Nedelec elements Hdiv conforming: NedelecFaceFirstTetrahedronPk for Nedelec first family of any order and NedelecFaceSecondTetrahedronPk for Nedelec second family of any order. The second family is not yet available.
NedelecEdgeTetrahedron which implements the Nedelec elements Hrot conforming: NedelecEdgeFirstTetrahedronPk for Nedelec first family of any order and NedelecEdgeSecondTetrahedronPk for Nedelec second family of any order. The second family is not yet available.

Short identifiers of face/edge elements are defined in the following enumerations:

enum FeFaceType
{
 _RT_1 = 1, RT_1 = _RT_1, _NF1_1 = _RT_1, NF1_1 = _RT_1,
 _RT_2 ,    RT_2 = _RT_2, _NF1_2 = _RT_2, NF1_2 = _RT_2,
 _RT_3 ,    RT_3 = _RT_3, _NF1_3 = _RT_3, NF1_3 = _RT_3,
 _RT_4 ,    RT_4 = _RT_4, _NF1_4 = _RT_4, NF1_4 = _RT_4,
 _RT_5 ,    RT_5 = _RT_5, _NF1_5 = _RT_5, NF1_5 = _RT_5,
 _BDM_1 ,    BDM_1 = _BDM_1, _NF2_1 = _BDM_1, NF2_1 = _BDM_1,
 _BDM_2 ,    BDM_2 = _BDM_2, _NF2_2 = _BDM_2, NF2_2 = _BDM_2,
 _BDM_3 ,    BDM_3 = _BDM_3, _NF2_3 = _BDM_3, NF2_3 = _BDM_3,
 _BDM_4 ,    BDM_4 = _BDM_4, _NF2_4 = _BDM_4, NF2_4 = _BDM_4,
 _BDM_5 ,    BDM_5 = _BDM_5, _NF2_5 = _BDM_5, NF2_5 = _BDM_5
};

enum FeEdgeType
{
 _N1_1 = 1, N1_1 = _N1_1, _NE1_1 = _N1_1, NE1_1 = _N1_1,
 _N1_2 ,    N1_2 = _N1_2, _NE1_2 = _N1_2, NE1_2 = _N1_2,
 _N1_3 ,    N1_3 = _N1_3, _NE1_3 = _N1_3, NE1_3 = _N1_3,
 _N1_4 ,    N1_4 = _N1_4, _NE1_4 = _N1_4, NE1_4 = _N1_4,
 _N1_5 ,    N1_5 = _N1_5, _NE1_5 = _N1_5, NE1_5 = _N1_5,
 _N2_1 ,    N2_1 = _N2_1, _NE2_1 = _N2_1, NE2_1 = _N2_1,
 _N2_2 ,    N2_2 = _N2_2, _NE2_2 = _N2_2, NE2_2 = _N2_2,
 _N2_3 ,    N2_3 = _N2_3, _NE2_3 = _N2_3, NE2_3 = _N2_3,
 _N2_4 ,    N2_4 = _N2_4, _NE2_4 = _N2_4, NE2_4 = _N2_4,
 _N2_5 ,    N2_5 = _N2_5, _NE2_5 = _N2_5, NE2_5 = _N2_5
};

The naming convention is based on the FE periodic table. Note that there is an equivalence between NF1_k and RT_k (Raviart-Thomas), NF2_k and BDM_k (Brezzi-Douglas-Marini), N1_k and NE1_k and, N2_k and NE2_k.

Hint

NedelecEdgeTetrahedron and NedelecFaceTetrahedron classes use a general process to build shape functions as polynomials related to moment DoFs. To match DoFs on shared edge or shared face, the ascending numbering of vertices is implicitly used even if it is not in fact. This method is particular touchy in case of face DoFs of Nedelec Edge element. Indeed, such DoFs depend on the choice of two tangent vectors, generally two edges of faces of the reference tetrahedron that are mapped to some edges of physical element in a non-trivial way. To ensure a correct matching of such DoFs on a shared face, a rotation has to be applied to shape values to guarantee that they correspond to the same tangent vectors. This is the role of the member function NedelecEdgeFirstTetrahedronPk::rotateDofs.

Note that if the element vertex numbering and face vertex numbering are ascending, rotateDofs does nothing. This trick is commonly used to overcome this difficulty but as XLiFE++ makes no assumption on geometry, this DoFs rotation is mandatory.

More details on edge/face elements are provided in a specific paper.

Attention

Nedelec second families are not yet available.

Lagrange elements#

Fig. 132 Tetrahedron P1 Fig. 133 Tetrahedron P1	Fig. 134 Tetrahedron P2 Fig. 135 Tetrahedron P2
Fig. 136 Tetrahedron P3 Fig. 137 Tetrahedron P3	Fig. 138 Tetrahedron P4 Fig. 139 Tetrahedron P4

Nedelec edge elements#

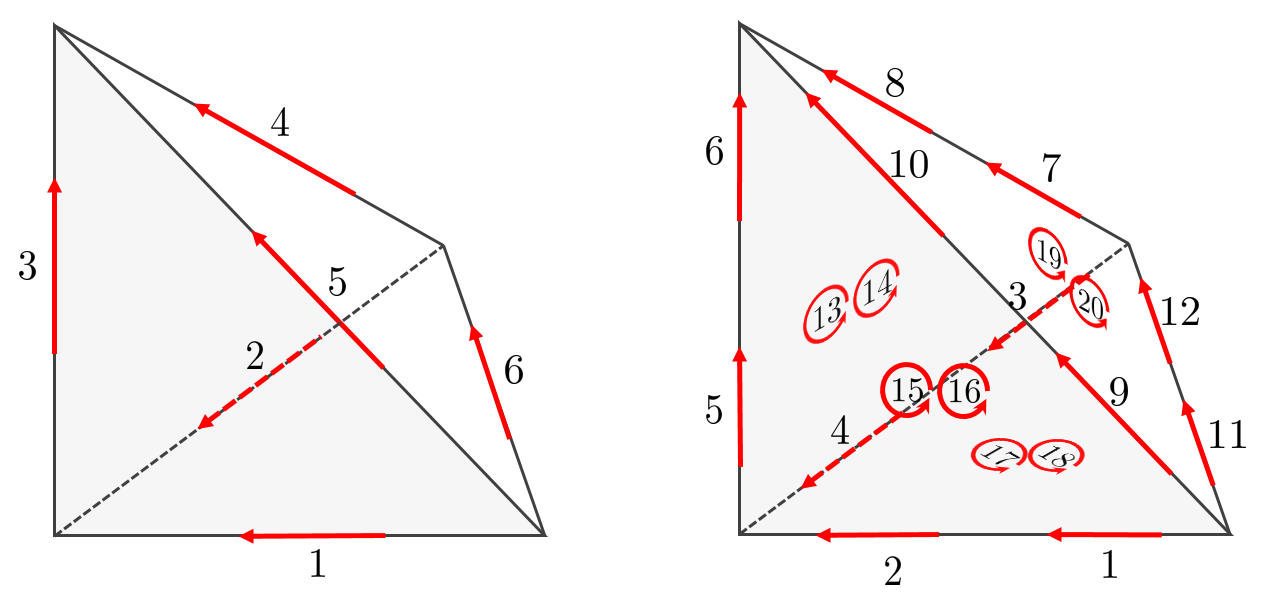
../../_images/NETet1_NETet2.png — Fig. 140 Nedelec edge elements (first family, order 1 and 2)#

Nedelec face elements#

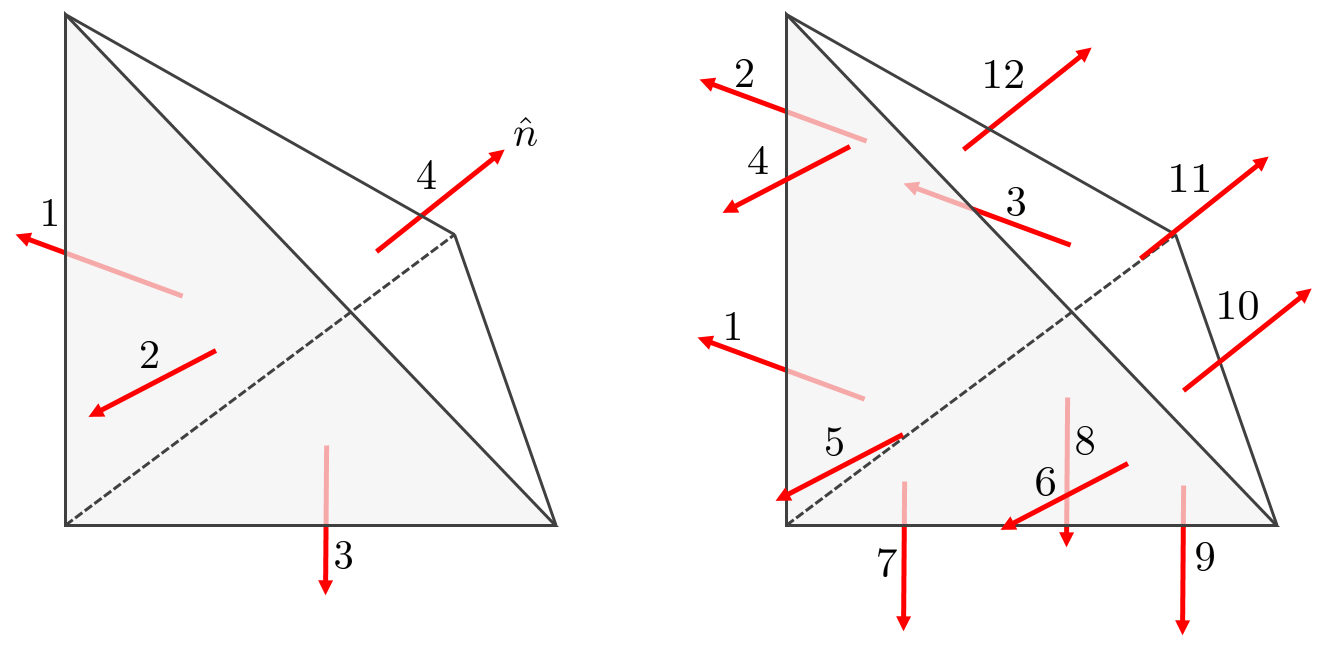
../../_images/NFT1_NFT2.png — Fig. 141 Nedelec face elements (first family, order 1 and 2)#

On hexahedron#

Figure made with TikZ

Lagrange elements#

Fig. 142 Hexahedron Q1: Fig. 143 Hexahedron Q1:	Fig. 144 Hexahedron Q2: Fig. 145 Hexahedron Q2:
Fig. 146 Hexahedron Q3: Fig. 147 Hexahedron Q3:

Nedelec edge elements#

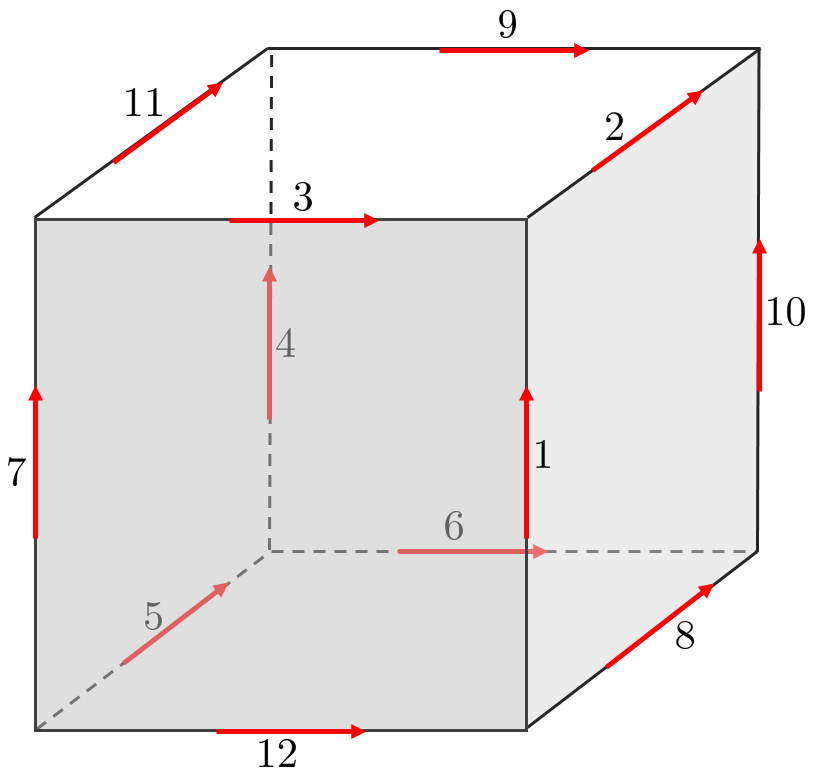
../../_images/NEHex1.png — Fig. 148 Nedelec edge elements (order 1)#

On prism#

Figure made with TikZ

Lagrange elements#

Figure made with TikZ

Fig. 149 Prism P1Q1:

Figure made with TikZ

Fig. 150 Prism P1Q1:

Figure made with TikZ

Fig. 151 Prism P2Q2:

Figure made with TikZ

Fig. 152 Prism P2Q2:

On pyramid#

Figure made with TikZ

Lagrange elements#

Figure made with TikZ

Fig. 153 Pyramid P1Q1:

Figure made with TikZ

Fig. 154 Pyramid P1Q1:

Figure made with TikZ

Fig. 155 Pyramid P2Q2:

Figure made with TikZ

Fig. 156 Pyramid P2Q2:

Reference element stuff#

The `RefElement` class#

The RefElement is the main class of the finiteElement library. It handles all the stuff related to a finite element defined on a reference geometry:

an Interpolation object managing finite element description,

a GeomRefElement object managing geometric data,

a collection of RefDof objects (degrees of freedom related to the finite element )

some collection of ShapeValues (values of shape functions related to the finite element)

It is the parent class of the wide range of true reference elements, identified by shape and interpolation type (see above). That is why it is a complex class collecting a lot of information and providing many numbering functions such as the number of DoFs, the same number on vertices, on sides, on side of sides, …:

class RefElement
{
 public:
  GeomRefElement* geomRefElem_p;        //pointer to geometric reference element
  const Interpolation* interpolation_p; //interpolation parameters
  vector<RefDof*> refDofs;              //local reference Degrees of Freedom
  FEMapType mapType;                    //type of map applied to shape functions
  DofCompatibility DoFCompatibility;    //compatibility rule to applied to side DoFs
  Dimen dimShapeFunction;               //dimension of shape function
  Number maxDegree;                     //maximum degree of shape functions
  bool rotateDof;                       //if true, apply rotation to shape values
 protected:
  String name_;                     //name (for documentation)
  Number nbDofs_;             //nb of Degrees Of Freedom
  Number nbPts_;              //nb of Points (for local coordinates of points)
  Number nbDofsOnVertices_;   //nb of sharable DoF on vertices (first DoF)
  Number nbDofsInSideOfSides_;//nb of sharable DoF on side of sides (edges)
  Number nbDofsInSides_;      //nb of sharable DoF on sides (faces or edges)
  Number nbInternalDofs_;     //nb of non-sharable DoF's
  vector<RefElement*> sideRefElems_;       //pointers to side reference elements
  vector<RefElement*> sideOfSideRefElems_; //pointers to side of side reference elements
 public:
  vector<vector<Number>> sideDofNumbers_;        //DoF numbers for each side
  vector<vector<Number>> sideOfSideDofNumbers_;  //DoF numbers for each side of side
  PolynomialsBasis Wk;                           //shape functions basis as polynomials
  vector<PolynomialsBasis> dWk;                  //derivatives of shape functions
  map<Quadrature*,vector<ShapeValues>> qshvs_;   //to store shape function values
  map<Quadrature*,vector<ShapeValues>> qshvs_aux;//to store shape function values
};

The FEMapType enumerates the types of affine mapping from reference element to any element. It depends on finite element type:

enum FEMapType {_standardMap,_contravariantPiolaMap,_covariantPiolaMap,_MorleyMap,_ArgyrisMap};

Most of the data are filled by inherited classes (true finite element class). Shape functions of high order element are boring to find. So, XLiFE++ provides tools to get them in a formal way, using Polynomials class. The virtual function computeShapeFunctions computes them and the buildPolynomialTree function builds a tree representation of the formal representation of shape functions, in order to make faster their computations.

This class drives the computation of shape function values, using the virtual member function:

void computeShapeValue(pt_iterator itp, ShapeValues& shv, bool withDer = true,
                                                     bool withwithDer2 = false);

The `Interpolation` class#

The purpose of the Interpolation class is to store data related to finite element interpolation. It concerns only general description of an interpolation:

type of the finite element interpolation (Lagrange, Hermite, …),
subtype among standard, Gauss-Lobatto (only for Lagrange) and first or second family (only for Nedelec),
the “order” of the interpolation
the space conformity (one of L2, H1, Hdiv, Hcurl, H2).

For instance, a Lagrange standard P1 with H1 conforming is the classic P1 Lagrange interpolation but a Lagrange standard P1 with L2 conforming means a discontinuous interpolation (like Galerkin discontinuous approximation) where the vertices of an element are not shared.

For the moment, this class is only intended to support the following choices, that correspond to the _FE_type, the _FE_subtype and the _order keys used in Space construction:

type	subtype	order
Lagrange	standard, Gauss-Lobatto	any order
Hermite	standard
Morley	standard	order 2
Argyris	standard	order 5
Crouzet-Raviart	standard	order 1
Raviart-Thomas	standard	any order
Nedelec	first or second family	any order
Nedelec face	first or second family	any order
Nedelec edge	first or second family	any order

Hint

Nedelec face and Nedelec edge are specific to 3D. Nedelec face corresponds to the 2D Raviart-Thomas family and Nedelec edge corresponds to the 2D Nedelec family.

Hint

The Interpolation class is intended to support a lot of finite element family, but all are not available. See child classes of RefElement class to know which families are actually available.

The class Interpolation has the following attributes:

class Interpolation
{
  public:
    const FEType type;        // interpolation type
    const FESubType subtype;  // interpolation subtype
    const Number numtype;     // additional number type (degree for Lagrange)
    SobolevType conformSpace; // conforming space
    String name;              // name of the interpolation type
    String subname;           // interpolation sub_name
    String shortname;         // short name (see build)
};

FEType, FESubType and SpaceType are enumerations defined in the config.hpp file as follows:

enum SobolevType{L2=0,H1,Hdiv,Hcurl,Hrot=Hcurl,H2,Hinf};
enum FEType {Lagrange,Hermite,CrouzeixRaviart,Nedelec,RaviartThomas,
             NedelecFace,NedelecEdge,_Morley,_Argyris};
enum FESubType  {standard=0,gaussLobatto,firstFamily,secondFamily};

Interpolation objects may be constructed in two ways:

Interpolation intp(Lagrange,standard,2,H1);                // using explicit constructor
Interpolation& intp=interpolation(Lagrange,standard,2,H1); // using implicit constructor

The `GeomRefElement` class#

The GeomRefElement class carries geometric data of a reference element: type, dimension, number of vertices, sides and side of sides, measure, and coordinates of vertices. Furthermore, to help to find geometric data on sides, it also carries type, vertex numbers of each side on the first hand, and vertex numbers and relative number to parent side of each side of side on the second hand:

class GeomRefElement
{
 protected:
  ShapeType shapeType_;     //element shape
  const Dimen dim_;         //element dimension
  const Number nbVertices_, nbSides_, nbSideOfSides_; //number of vertices, ...
  const Real measure_;                       //length or area or volume
  vector<Real> centroid_;                    //coordinates of centroid
  vector<Real> vertices_;                    //coordinates of vertices
  vector<ShapeType> sideShapeTypes_;         //shape type of each side
  vector<vector<Number> > sideVertexNumbers_;
  vector<vector<Number> > sideOfSideVertexNumbers_;
  vector<vector<Number> > sideOfSideNumbers_;
};

This class proposes various functions to get geometrical information and has has child classes :

GeomRefSegment in 1D,
GeomRefTriangle and GeomRefQuadrangle in 2D
GeomRefHexahedron, GeomRefTetrahedron, GeomRefPrism and GeomRefPyramid in 3D.

that propose specific numbering functions.

The `RefDof` class#

The RefDof class handles the representation of a generalized degree of freedom in a reference element. It manages:

A support that can be a point, a side, a side of side or the whole element. When it is a point, its coordinates are available.
A dimension, that means the number of components of shape functions of the DoF.
Projections data (type and direction) when the DoF is a projection DoF. The projection type is 0 for a general projection, 1 for a $u . n$ DoF, 2 for a $u \times n$ DoF.
Derivative data (order and direction) when the DoF is a derivative DoF. The order is 0 when the DoF is defined by an ‘integral’ over its support, or $n$ for a Hermite DoF derivative of order $n > 0$ or a moment DoF of order $n > 0$ .
A shareable property: a DoF is shareable when it is shared between adjacent elements according to space conformity. Such a DoF can be shared or not according to interpolation. For example, every DoFs of a Lagrange H1-confirming element on a side is shared, while DoFs in discontinuous interpolation are not.

class RefDof
{
 private:
  RefElement* refElt_p;      // pointer to refElement related to current refdof
  bool sharable_;            // DoF is shared according to space conformity
  DofLocalization where_;    // hierarchic localization of DoF
  Number supportNum_;        // support localization
  Number index_;             // rank of the DoF in its localization
  Dimen supportDim_;         // dimension of the DoF geometric support
  Number nodeNum_;           // node number when a point DoF
  Dimen dim_;                // number of components of shape functions of DoF
  std::vector<Real> coords_; // coordinates of DoF support if supportDim_=0
  Number order_;             // order of a derivative DoF or a moment DoF
  String name_;                        // DoF-type name for documentation
  ProjectionType projectionType_;      // type of projection
  std::vector<Real> projectionVector_; // direction vector(s) of a projection
  DiffOpType diffop_;                  // DoF differential operator (_id,_dx,_dy, ...)
  std::vector<Real> derivativeVector_; // direction vector(s) of a derivative

}

RefDof objects are created by the child classes of RefElement (specific finite element classes).

Hint

For non-nodal DoFs (supportDim_>0), virtual coordinates are also defined. They are useful when dealing with essential conditions.

Hint

Up to now, derivative vectors are not used, and the normal vector involved in $n . \nabla$ DoFs is stored in the projection vector.

The `ShapeValues` class#

A ShapeValues object stores the values of shape functions at a given point. Thus, it carries 2 real vectors of:

class ShapeValues
{
 public:
  vector<Real> w;          //shape functions at a point
  vector<vector<Real>> dw; //first derivatives (dx,[dy,[dz]])
  vector<vector<Real>> d2w;//2nd derivatives   (dxx,[dyy,dxy,[dzz,dxz, dyz]])
 ...
};

This class also drives the mapping of shape functions according to the mapping type (FEMapType):

void map(ShapeValues&,GeomMapData&,bool der1,bool der2);  //standard mapping
void contravariantPiolaMap(ShapeValues&,GeomMapData&,bool der1,bool der2);
void covariantPiolaMap(ShapeValues&,GeomMapData&,bool der1,bool der2);
void Morley2dMap(ShapeValues&,GeomMapData&,bool der1,bool der2);
void Argyris2dMap(ShapeValues& rsv,GeomMapData& gd,bool der1,bool der2);
void changeSign(vector<Real>& sign, Dimen); //change sign of shape functions according to a sign vector

The contravariant and covariant Piola maps are respectively used for Hdiv and Hcurl finite element families. They preserve respectively the normal and tangential traces. If $J$ denotes the jacobian of the mapping from the reference element to any element, $\hat{u}$ a vector field in the reference space:

the covariant map is $J^{- t} \hat{u}$
the contravariant map $J \hat{u} / | J |$
the Morley and Argyris map are specific to these elements. They preserve first and second derivatives involved in such elements.

Finite elements#

On segment#

On triangle#

Lagrange elements#

Raviart-Thomas elements#

Nedelec edge elements#

On quadrangle#

Lagrange elements#

Nedelec edge elements#

On tetrahedron#

Lagrange elements#

Nedelec edge elements#

Nedelec face elements#

On hexahedron#

Lagrange elements#

Nedelec edge elements#

On prism#

Lagrange elements#

On pyramid#

Lagrange elements#

Reference element stuff#

The RefElement class#

The Interpolation class#

The GeomRefElement class#

The RefDof class#

The ShapeValues class#

The `RefElement` class#

The `Interpolation` class#

The `GeomRefElement` class#

The `RefDof` class#

The `ShapeValues` class#