`SplineSurface`#

A spline surface is a geometrical surface in 3D built from a Nurbs object (see Spline surface (nurbs)) implicitly parametrized by two scalars \((u,v)\in[0,1]\times[0,1]\). It has at most 4 sides (some may be degenerated).

A SplineSurface geometry may be either constructed directly from a Nurbs object:

Number nbu=7, m= 2*nbu+1, n=nbu+1;
Real ds=pi_/(2*nbu); Real u=-pi_/2,v;
Points pts(m*n);
for(Number i=0;i<=2*nbu;i++,u+=ds)
{
  v=0;
  for(Number j=0;j<=nbu;j++,v+=ds)
    pts[i*n+j]=Point(cos(u)*cos(v),cos(u)*sin(v),sin(u));
}
Nurbs nuI(_splineInterpolation,pts,m,);  // interpolation nurbs
SplineSurface spsI(_spline=nuI, _hsteps=0.2, _domain_name="Omega",
                   _side_names={"Gamma1","Gamma2","Gamma3","Gamma4"});

or using parameter keys:

SplineSurface sps(_vertices=pts, _nbu=m, _hsteps=0.2, _domain_name="Omega",
                  _side_names={"Gamma1","Gamma2","Gamma3","Gamma4"});

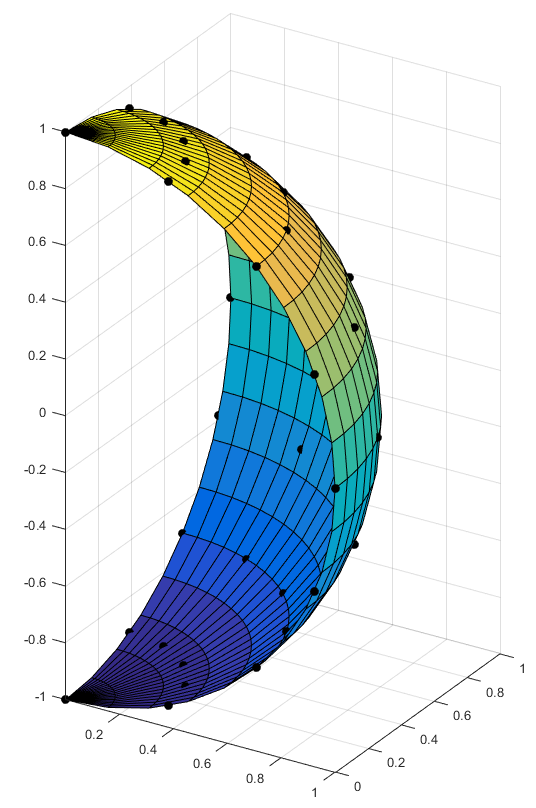
Sides names order rule is \(v=0\), \(u=1\), \(v=1\) and \(u=0\). In the previous example, because some bound points collapse, there are only two sides really named (\(v=0\) and \(v=1\)), , corresponding to “Gamma1” and “Gamma3”.

Important

By using the option _splineApproximation, it is also possible to address approximation splines.

In addition to the standard keys (_hsteps, _domain_name, …) the following keys are available:

key(s)	authorized types	examples
`_spline`	`Nurbs`	`_spline=nu`
`_splineSubtype`	_splineInterpolation or _splineApproximation	`_splineSubtype=_splineInterpolation`
`_vertices`	`Point` vector (`Points`)	`_vertices =pts`
`_weights`	`Real` vector (`Reals`)	`_weights=ws`
`_nbu`	unsigned int (`Number`)	`_nbu =5`

Warning

Do not forget to specify the value nbu (either in Nurbs construction or in key) that specifies the number of control/interpolation points in u-direction; the number of points in v-direction is deduced from the size of control/interpolation point vector. It should be a multiple of nbu!

Danger

Up to now, such SplineSurface geometry can be meshed only with the OpenCascade engine!

Hint

Parametrization of the spline surface is related to the Spline class parametrization (see Splines)

SplineSurface#

`SplineSurface`#