H-matrices#

The hierarchicalMatrix library deals with large matrices that are represented by a hierarchical tree, each tree node being either a real submatrix (leaf) or a virtual submatrix addressing up to four nodes:

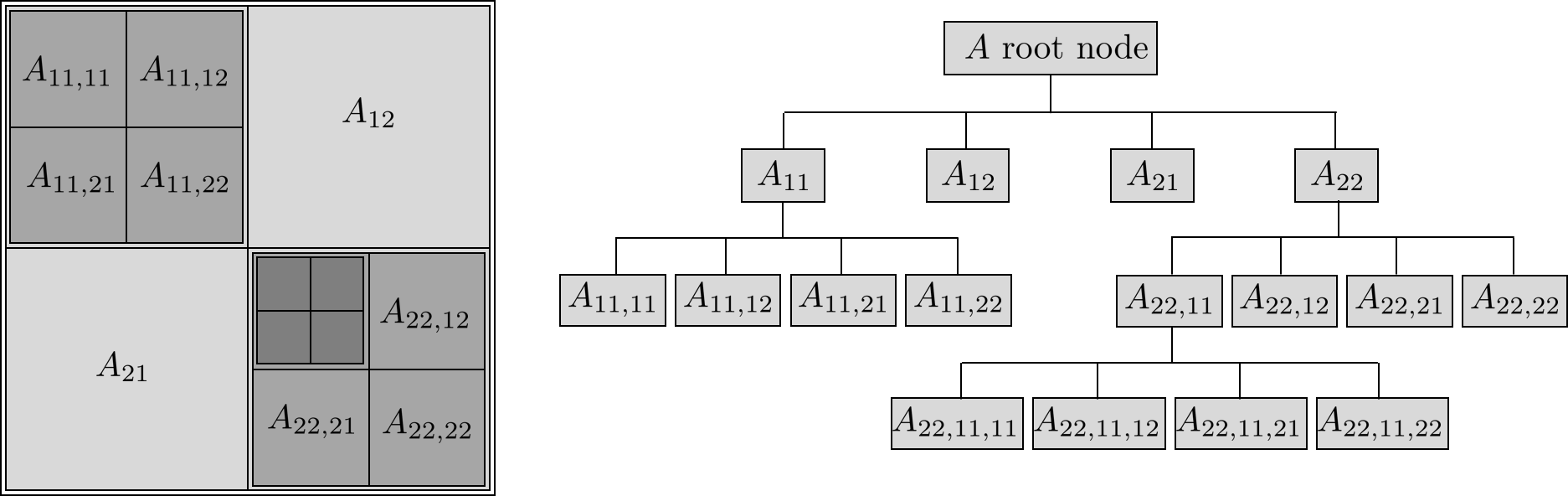
HMatrix1 — Fig. 145 Hierarchical matrix#

The matrix may be not squared and therefore the submatrices too.

Such representation comes from mesh partition (clustering) where far interactions in BEM may be approximated by low rank matrices, so reducing the storage of matrix and making the matrix vector product faster. The hierarchicalMatrix library proposes

some template classes to deal with clusters of Points, FeDofs, Elements, … : ClusterTree and ClusterNode
some template classes to deal with approximated matrices: ApproximateMatrix<T> and LowRankMatrix<T>
some template classes addressing hierarchical matrices: HMatrix<T, I>, HMatrixNode<T,I> and HMatrixEntry

Cluster tree#

The clustering of a set of objects consists in a partition of this set with a hierarchical structure. Each node of the cluster being a subset of the parent node subset. The partitioning of a subset is done according to some rules depending on the purpose of the cluster.

In the case of a mesh, we are interested in clusters of points (mesh nodes) or in clusters of elements where the partitioning rule aims to separate geometrically the points or the elements.

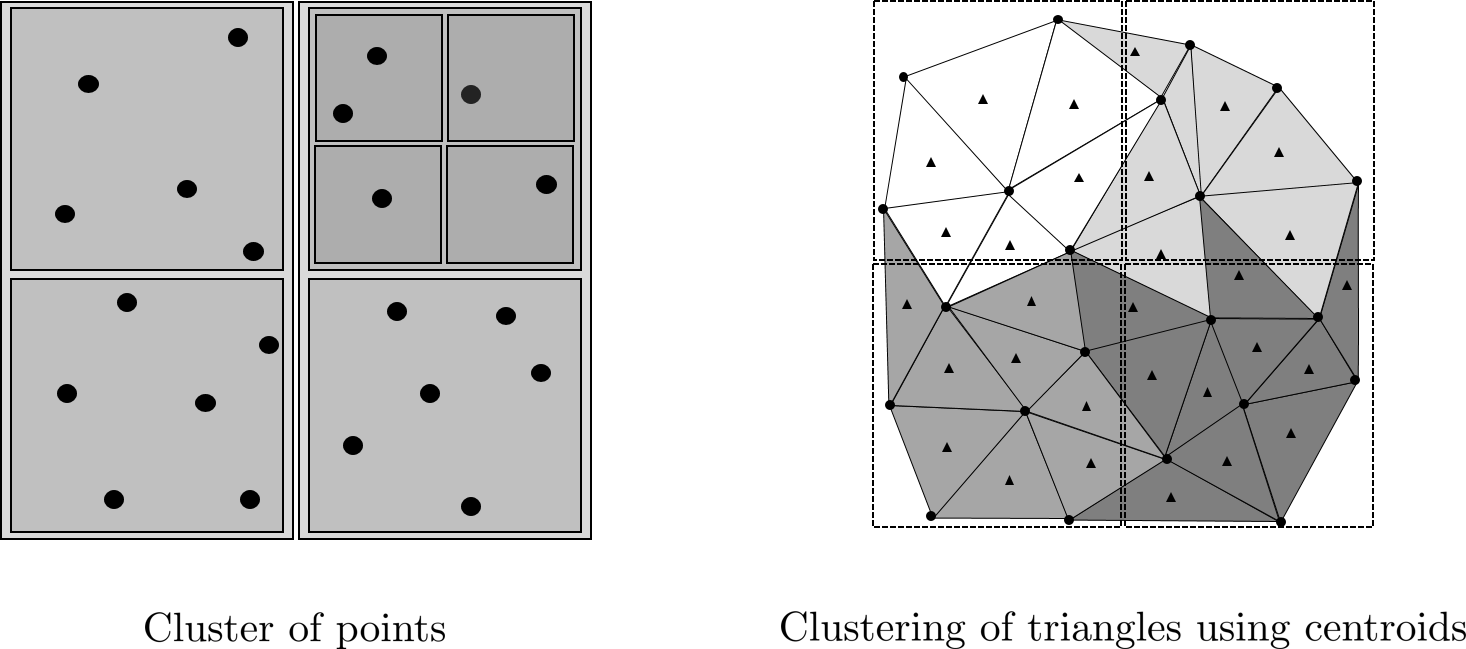
XLiFE++ provides two classes templated by the type I of objects to be clustered:

ClusterNode managing one node of the tree representation
ClusterTree managing the tree representation from the root node

The `ClusterNode<T>` class#

The ClusterNode class describes one node of the tree representing the cluster where I is the type of objects to be clustered. It is assumed that I is a geometric object and that the three following functions are available:

Dimen dim(const T&) const;               //dimension of T object
Real coords(const T&, Number i) const  //i-th coordinates of T object
BoundingBox boundingBox(const T &)         //xy(z) bounding box of T object

For instance, these functions are provided for the XLiFE++ classes : Point, FeDof, Element allowing to cluster mesh using either some points of mesh (vertices), some finite element DoFs or some finite elements.

The class manages standard information:

vector<T>* objects_;      //pointer to the list of all objects
vector<Number> numbers_;//object numbers related to objects_ vector
ClusterNode* parent_;     //pointer to its parent (0 for root node)
ClusterNode* child_;      //pointer to its first child (0 = no child)
ClusterNode* next_;       //pointer to its brother, (0 = no brother)
Number depth_;          //depth of node/leaf in tree (0 for root node)
BoundingBox boundingBox_;        //bounding box from characteristic points
BoundingBox realBoundingBox_;    //bounding box from bounding boxes of objects

The list of objects belonging to the cluster node is given by the Numbers vector that stores the indices of objects in the vector objects_. The clusters we deal with are supposed to be geometrical clusters and the clustering methods are mainly based on splitting of boxes, it is the reason why the class deals explicitly with bounding boxes. In the context of finite element, some additional data (mutable) can be handled:

vector<Number> DoFNumbers_;  //list of DoF numbers related to the node
vector<Element*> elements_;    //list of element numbers related to the node

The class provides only one constructor assigning fundamental data ( objects_, parent_, child_, next_, depth_) and a clear method that deletes recursively the subtree from the current node:

ClusterNode(vector<T>*,ClusterNode*,Number, ClusterNode*=0, ClusterNode*=0);
void clear();

Hint

The copy constructor and assignment operator are the default ones, so the tree structure is not duplicated but only shared. Be cautious, when you use copy or assignment.

The class provides some functions to get some properties or data:

Number dimSpace() const;   //geometric dimension
Number size() const;       //number of objects
bool isVoid() const;         //true if void node
vector<ClusterNode*> getLeaves() const; //list of leave pointers
list<Number> getNumbers(bool) const;  //list of Numbers (recursive)
const BoundingBox& box() const;     //return the real bounding box if allocated
Real boxDiameter() const;         //diameter ot the (real) bounding box

The main member function that builds the tree structure from a division process is:

void divideNode(ClusteringMethod cm, Number mininleaf, Number maxdepth=0, bool store = true);

where

ClusteringMethod is the enumeration of clustering methods:
```
enum ClusteringMethod { _regularBisection, _boundingBoxBisection, _cardinalityBisection, _uniformKdtree, _nonuniformKdtree };
```
Except the _uniformKdtree and _nonuniformKdtree methods, all others are bisection method in the direction where the boxes are larger, so the tree is a binary one. _regularBisection split boxes in two boxes of the same size, _boundingBoxBisection split bounding boxes of objects in two boxes of the same size, _cardinalityBisection split boxes in two boxes such that all new boxes have the same number of objects. The trees produced by this last method are better balanced. The _uniformKdtree and _nonuniformKdtree methods split any boxes in 2, 4 or 8 sub-boxes regarding the space dimension (1, 2 or 3); the sub-boxes are of the same size in any direction. Thus, it produces binary tree in 1D, quadtree in 2D and octree in 3D. With _uniformKdtree method, all the boxes at the same level have the same size whereas with _nonuniformKdtree method, all the boxes are the minimal bounding boxes defined from the objects that they embed.

maxinleaf is the maximum of objects in a leaf node, more precisely, a node is divided when its number of objects is greater than maxinleaf.
maxdepth, if not null, allows to stop the division process when maxdepth is reached. This stopping criterion has priority over the previous criteria.
if store parameter is true, data (numbers_}, bounding boxes, …) are stored for each node else they are only stored for each leaves. By default, its value is true, but if cluster is too large, not storing some data may save memory but some algorithms working on clusters could be slower.

Hint

Up to now, only three clustering methods are offered, but it is quite easy to add a new one by handling a new case in divideNode function. Bisection methods build binary tree, but there is no limitation of the number of children in the ClusterNode class!

When some data (numbers_, bounding boxes, …) are not available it is possible to build or update it:

void setBoundingBox();           //set the bounding box
void setRealBoundingBox();       //set the real bounding box
void updateRealBoundingBoxes();  //update recursively real bounding boxes
void updateNumbers();            //update numbers_ vector

When dealing with finite elements some additional data may be useful, in particular the link between DoFs and elements. To avoid costly re-computation, it may be clever to store it. The following member functions do the job on demand when working with a ClusterNode<FeDof> or a ClusterNode<Element>:

const vector<Number>& DoFNumbers() const; //access to DoFNumbers
const vector<Element*>& elements() const;   //access to elt pointers
vector<Number> getDofNumbers(bool=false) const; //list of DoF numbers
vector<Element*> getElements(bool=false) const;   //list of elt numbers
void updateDofNumbers();                   //update recursively DoFNumbers
void updateElements();                     //update recursively elements
Number nbDofs() const;                   //number of DoFs

Finally, there are some stuff to print and save to file node information:

void printNode(std::ostream&, bool shift=true) const; //print node
void print(std::ostream&) const;         //print tree from current node (recursive)
void printLeaves(std::ostream&) const;   //print leaves of the tree
void saveToFile(const String&, bool) const; //save bounding boxes to file
friend ostream& operator<<(std::ostream&, const ClusterNode<T>&);

The `ClusterTree<T>` class#

The ClusterTree<T> class is the front end of ClusterNode<T> class which supports the tree structure of the cluster. Because the ClusterTree<T> class interfaces most data and functionalities of the ClusterNode<T> class, for explanation go to the previous section.

The ClusterTree<T> class manages the parameters and information required or provided by the ClusterTree<T> class. It handles the tree structure (the cluster) through the root node pointer:

template <typename T = FeDof> class ClusterTree
{
  public:
   vector<T>* objects_;       //pointer to a list of objects
   ClusteringMethod method_;  //clustering method
   Number maxInBox_;        //maximum number of objects in a leaf
   Number depth;            //depth of the tree
   bool storeNodeData_;       //store data on each node if true
   bool clearObjects_;        //if true deallocate vector objects_ when clear
   Number nbNodes;          //number of nodes (info)
   Number nbLeaves;         //number of leaves (info)
   bool withOverlap_;         //true if DoF numbering of nodes overlap
   bool noEmptyBox_;          //do not keep empty boxes in tree
  private:
   ClusterNode<T>* root_;     //root node of cluster
  ...
}

Note that the ClusterTree has FeDof object as template default argument. This is the standard cluster used by the HMatrix class presented in a next section.

This class provides a unique constructor, building the cluster from a list of geometric object, a clustering method, the maximal depth of the tree, the maximal number of objects in leaf node and a flag telling if empty leaf nod are removed from the tree:

ClusterTree(const vector<T>&, ClusteringMethod, Number depth, Number maxinleaf=0, bool store=true, bool noemptybox = true);

Hint

The copy constructor and assignment operator are the default ones, so the tree structure is not duplicated but only shared. Be cautious, when you use copy or assignment. In particular avoid destruction of ClusterTree object, except if you set the member data clearObjects to false before destroy it.

Almost all the member functions are interface to their equivalent in ClusterNode class:

ClusterNode<T>* root();
void setOverlap();
void updateBoundingBoxes();            //update recursively bounding boxes
void updateRealBoundingBoxes();        //update recursively real bounding boxes
void updateNumbers();                  //update recursively Numbers_ vector
void updateDofNumbers();               //update recursively DofNumbers_ vector
void updateElements();                 //update recursively Elements_ vector
void updateInfo();                     //update tree info (depth, ...)
Number nbDofs() const;
void print(ostream&) const;            //print tree
void printLeaves(ostream&) const;      //print only leaves
void saveToFile(const String&,
bool withRealBox= false) const; //save (real) bounding boxes to file
ostream& operator<<(ostream& out, const ClusterTree<T>&);

For instance, to generate a cluster of a disk mesh, write :

Disk disk(_center=Point(0.,0.), _radius=1., _nnodes=16, _domain_name="Omega");
Mesh mesh(disk, _generator=gmsh);
Domain omg=mesh.domain("Omega");
Space V(_domain=omg, _interpolation=P0, _name="V", _notOptimizeNumbering);
ClusterTree<FeDof> clt(V.feSpace()->DoFs,_regularBisection,10);
clt.saveToFile("cluster_disk.txt");

As the DoFs of P0 approximation are virtually located at the centroids of triangles, clustering of FeDof is equivalent to the clustering of centroids.

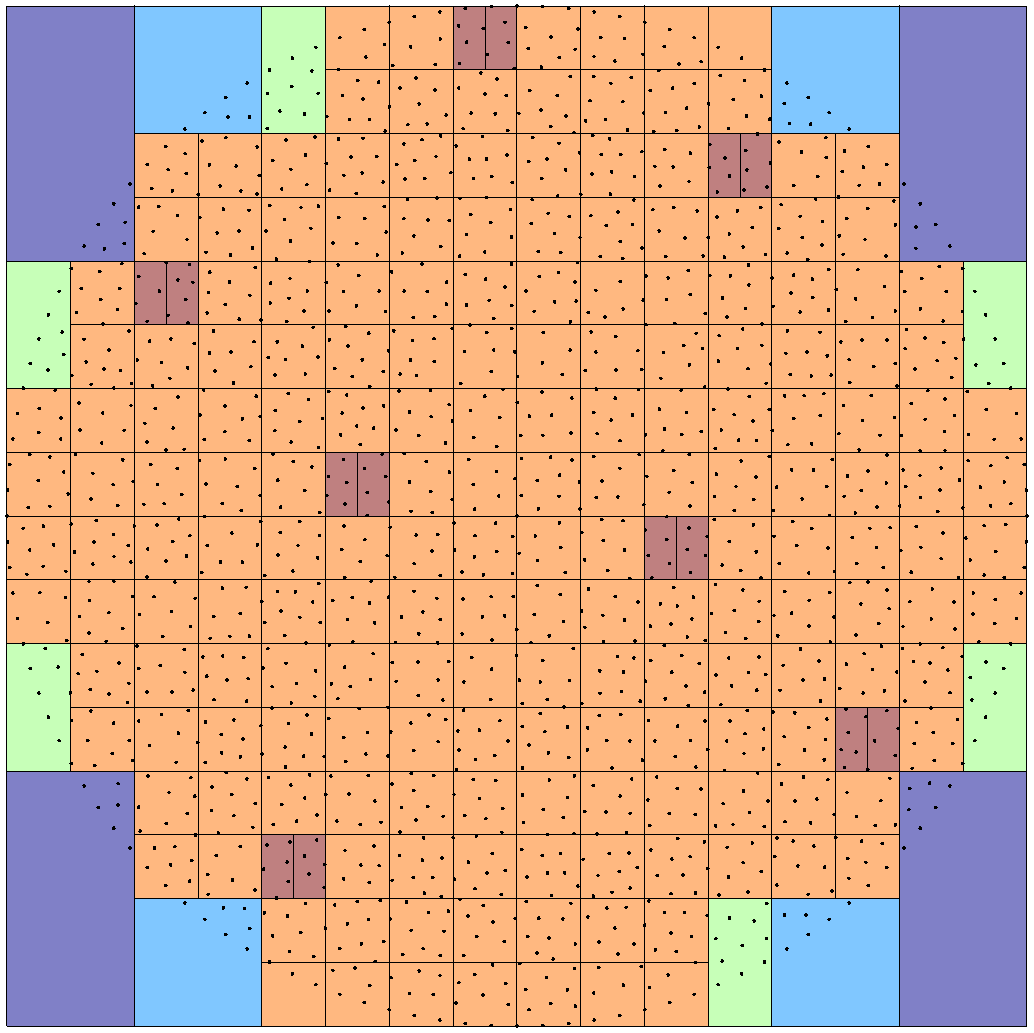
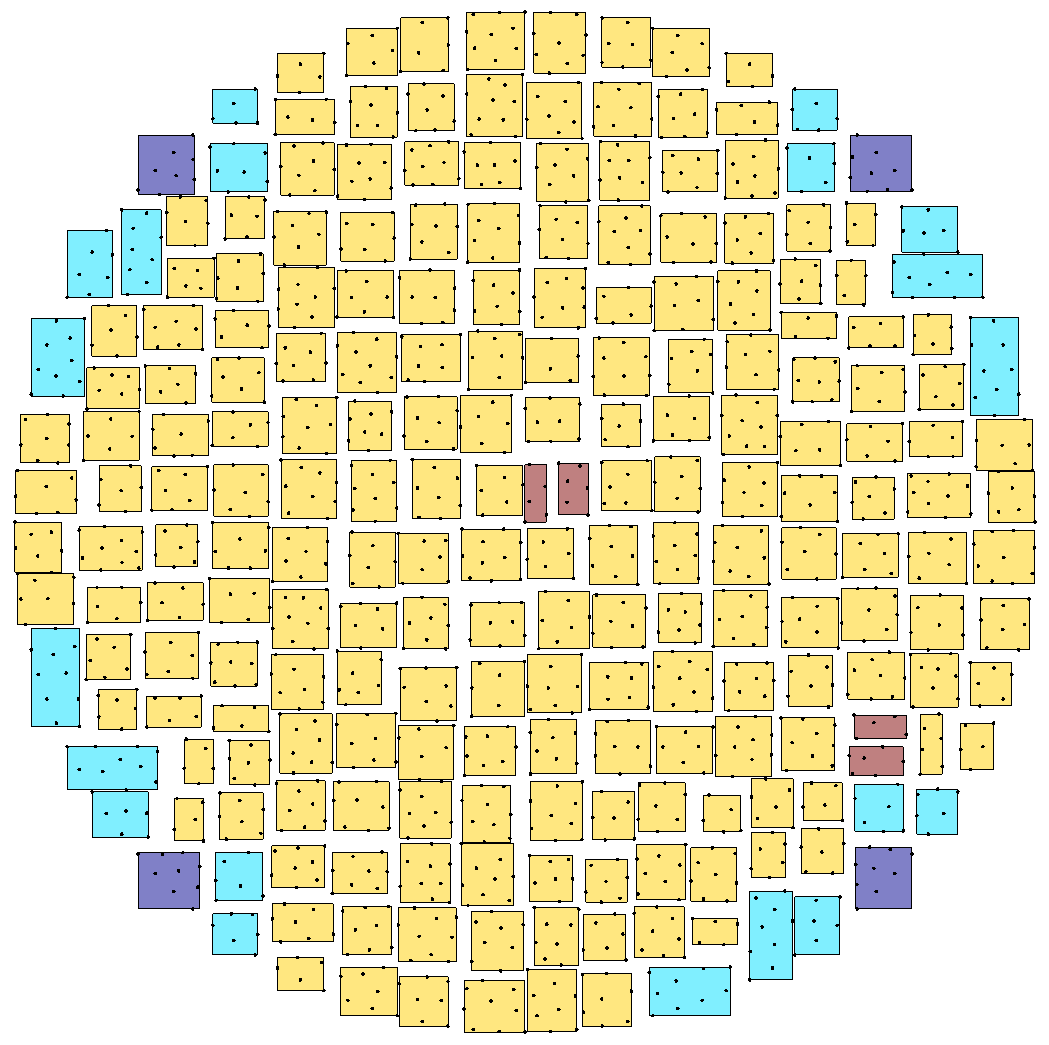
We show on the figure Clustering of a disk mesh using regular, bounding box and cardinality bisection methods the clustering of a disk mesh (1673 nodes) with maximum of 10 nodes by box, using regular method, boundingbox, cardinality bisection methods. Only boxes of leaves are displayed; different colors correspond to different node depths.

regular cluster — Fig. 146 Clustering of a disk mesh using regular, bounding box and cardinality bisection methods#

bounding cluster — Fig. 146 Clustering of a disk mesh using regular, bounding box and cardinality bisection methods#

uniform Kdtree — Fig. 147 Clustering of a disk mesh using kdtree methods#

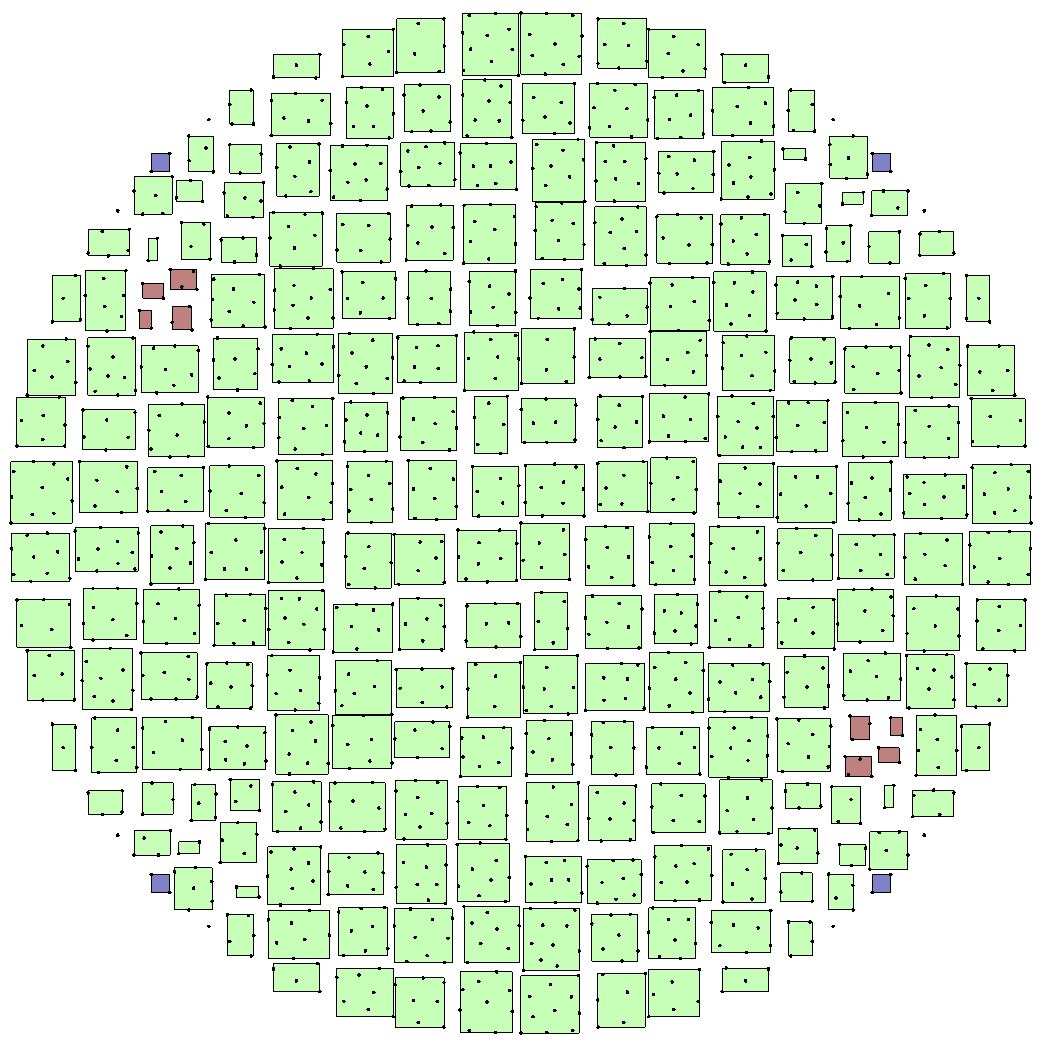
non uniform Kdtree — Fig. 147 Clustering of a disk mesh using kdtree methods#

Approximate matrix#

In the context of hierarchical matrix, some sub-matrices may be “compressed” to save memory and time computation. XLiFE++ provides a general class ApproximateMatrix to deal with real or complex approximate matrix that can be

low rank matrix represented as the product \(UDV^*\) (LowRankMatrix)
sinus cardinal decomposition (SCDMatrix), not yet available
fast multipole representation (FMMMatrix), not yet available

The `ApproximateMatrix` class#

The ApproximateMatrix class is a template abstract class (templated by the type of coefficients) that manages only the type of approximation, the name of the approximate matrix and defines all virtual functions that children has to implement:

template <typename T>
class ApproximateMatrix
{
  public :
   MatrixApproximationType approximationType;     //type of approximation
   String name;                                 //optional name useful for doc
   virtual ~ApproximateMatrix() {};               //virtual destructor
   virtual ApproximateMatrix<T>* clone() const=0; //creation of a clone
   virtual Number numberOfRows() const =0;      //nb of rows
   virtual Number numberOfCols() const =0;      //nb of columns
   virtual Number nbNonZero() const =0;         //nb of nonzeros coefficient
   virtual Number rank() const =0;              //rank of matrix
   virtual vector<T>& multMatrixVector(const vector<T>&, vector<T>&) const = 0;
   virtual vector<T>& multVectorMatrix(const vector<T>&, vector<T>&) const = 0;
   virtual Real norm2() const =0;                  //Frobenius norm
   virtual Real norminfty() const=0;               //infinite norm
   virtual LargeMatrix<T> toLargeMatrix() const = 0; //convert to LargeMatrix
   virtual void print(std::ostream&) const =0;       //print to stream
};

Up to now, the only children available is the templated LowRankMatrix<T> class.

The `LowRankMatrix<T>` class#

A low rank matrix is a matrix of the form

\[U\,D\,V^*\]

where \(U\) is an \(m\times r\) matrix, \(V\) is an \(n\times r\) matrix and \(D\) is an \(r\times r\) diagonal matrix. The rank of a such matrix is at most \(r\). So it is a low rank representation of an \(m\times n\) matrix if \(r\) is small compared to \(m\), \(n\). Contrary to the class name suggests, some matrix may be not low rank representation. Think about the SVD (singular value decomposition) of an \(m\times n\) matrix that can be handled by this class (\(r=\min(m,n)\)).

The LowRankMatrix class is derived from the ApproximateMatrix and handles the \((U,V)\) matrices as Matrix objects of XLiFE++ (dense matrix with major row access) and the diagonal matrix \(D\) as a Vector object of XLiFE++ :

template <typename T>
class LowRankMatrix : public ApproximateMatrix<T>
{
  public :
   Matrix<T> U_, V_;
   Vector<T> D_;
  ...
}

Different constructors are available:

LowRankMatrix();    //default constructor
//constructor from explicit matrices and vector
LowRankMatrix(const Matrix<T>&, const Matrix<T>&, const Vector<T>&, const String& na="");
LowRankMatrix(const Matrix<T>&, const Matrix<T>&, const String& na="");
//constructor from dimensions
LowRankMatrix(Number m, Number n, Number r, const String& na="");
LowRankMatrix(Number m, Number n, Number r, bool noDiag, const String& na="");
//constructor from matrix iterators and vector iterator
template <typename ITM, typename ITV>
LowRankMatrix(Number m, Number n, Number r, ITM itmu, ITM itmv, ITV itd, const String& na="");
template <typename ITM>
LowRankMatrix(Number m, Number n, Number r, ITM itmu, ITM itmv, const String& na="");

The LowRankMatrix class provides all virtual functions declared by the ApproximateMatrix class:

ApproximateMatrix<T>* clone() const;
Number numberOfRows() const;
Number numberOfCols() const;
Number nbNonZero() const;
Number rank() const;
bool hasDiag() const;
vector<T>& multMatrixVector(const vector<T>&, vector<T>&) const;
vector<T>& multVectorMatrix(const vector<T>&, vector<T>&) const;
LargeMatrix<T> toLargeMatrix() const;
Real norm2() const;
Real norminfty() const;
void print(std::ostream&) const;

In addition, the class offers specific algebraic operations as member functions:

LowRankMatrix<T> svd(Real eps) const;
LowRankMatrix<T>& operator+=(const LowRankMatrix<T>&);
LowRankMatrix<T>& operator-=(const LowRankMatrix<T>&);
LowRankMatrix<T>& operator*=(const T&);
LowRankMatrix<T>& operator/=(const T&);
LowRankMatrix<T>& add(const LowRankMatrix<T>&, const T&, Real eps=0);

and as external functions to the class (template declaration is omitted):

LowRankMatrix<T> combine(const LowRankMatrix<T>&, const T&, const LowRankMatrix<T>&, const T&, Real eps=0);
LowRankMatrix<T> operator+(const LowRankMatrix<T>&, const LowRankMatrix<T>&);
LowRankMatrix<T> operator-(const LowRankMatrix<T>&, const LowRankMatrix<T>&);
LowRankMatrix<T> operator-(const LowRankMatrix<T>&);
LowRankMatrix<T> operator+(const LowRankMatrix<T>&);
LowRankMatrix<T> operator*(const LowRankMatrix<T>&, const T&);
LowRankMatrix<T> operator/(const LowRankMatrix<T>&, const T&);
LowRankMatrix<T> operator*(const T&, const LowRankMatrix<T>&);

Note that the combination of a low rank matrix \(L_1=U_1D_1V_1\) of rank \(r_1\) and a low rank matrix \(L_2=U_2D_2V_2\) of rank \(r_2\) produces a low rank matrix \(L=U\,D\,V\) of rank \(r=r_1+r_2\) because

\[\begin{split}L=a_1L_1+a_2L_2=\left[\begin{array}{cc}U_1 & U_2\end{array}\right] \left[\begin{array}{cc} a_1D_1 & 0 \\ 0 & a_2D_2 \end{array}\right] \left[\begin{array}{c}V_1\\ V_2\end{array}\right].\end{split}\]

When nonzero, the eps argument in the LowRankMatrix::add and combine functions is used to re-compress the combined matrix with a truncated svd.

Finally, some compression methods based on SVD are implemented too. These compression methods “produce” a LowRankMatrix from a dense matrix stored in major column access and passed by a pointer to its first coefficient (template declaration is omitted):

void svdCompression(T* mat, Number m, Number n, Number r, LowRankMatrix<T>& lrm);
void svdCompression(T* mat, Number m, Number n, Real eps, LowRankMatrix<T>& lrm);
void rsvdCompression(T* mat, Number m, Number n, Number r, LowRankMatrix<T>& lrm);
void rsvdCompression(T* mat, Number m, Number n, Real eps, LowRankMatrix<T>& lrm);
void r3svdCompression(T* mat, Number m, Number n, Real eps, LowRankMatrix<T>& lrm, Number t = 0, Number p = 0, Number q = 0,  Number maxit = 0)

The SVD compression functions do the full svd of the given matrix and then truncate the number of singular values and singular vectors keeping either the \(r\) largest singular values/vectors or the singular values greater than a given eps. The fact that this process leads to a good approximate matrix results from the Eckart–Young–Mirsky theorem.

As the full svd is an expansive algorithm time computation, some alternative methods based on the random svd are also available. Random svd consists in capturing the matrix range using only few gaussian random vectors and doing a svd on a smaller matrix. Again, two versions of random svd are available, one providing a low rank matrix of a given rank, the other one providing a low rank matrix with a control on the approximate error. This last method iterates on the rank, so it is more expansive. The r3svd is a more sophisticated iterative method (see R3SVD).

Hint

As svd and qr algorithms have not been implemented for the \(Matrix\) class, XLiFE++ uses the Eigen library that is provided when installing XLiFE++.

Warning

svd, rsvd and aca compression does not work for matrix of matrices!

H-matrices#

Cluster tree#

The ClusterNode<T> class#

The ClusterTree<T> class#

Approximate matrix#

The ApproximateMatrix class#

The LowRankMatrix<T> class#

The `ClusterNode<T>` class#

The `ClusterTree<T>` class#

The `ApproximateMatrix` class#

The `LowRankMatrix<T>` class#