`SplineArc`#

SplineArc is the geometry class describing curves constructed from spline functions, either C2-spline (C2Spline), Catmull-Rom (CatmullRomSpline), Bézier spline (BezierSpline) or B-spline (BSpline), see Splines.

The mandatory keys to build a SplineArc geometry are:

key(s)	authorized types	examples
`_splineType`	_CatmullRomSpline, _C2Spline, _BezierSpline, _BSpline	`_splineType =_BSpline`
`_splineSubtype`	_splineInterpolation, _splineApproximation	`_splineSubtype =_splineInterpolation`
`_vertices`	vector of `Point`	`std::vector<xlifepp::Point> vp; ... _vertices=vp`

Important

To close a curve, the last point must be equal to the first one.

Warning

_splineSubtype concerns only BSpline and _splineInterpolation is the default value in that case.

Warning

The standard factory of GMSH does not support the C2-spline. It is available in OpenCASCADE machinery of GMSH which is not yet addressed by XLiFE++.

Besides standard keys (_name , _names , _hsteps , _nnodes), all the parameters of spline classes may be addressed with the following keys:

key(s)	authorized types	examples
`_splineBC`	_naturalBC, _clampedBC, _periodicBC	`_splineBC = _naturalBC`
`_tangent0` , `_tangent1`	`Reals`	`_tangent0 = Reals(1.,0.)`
`_degree`	integer value	`_degree =3`
`_tensionFactor`	real value	`_tensionFactor=0.5`
`_splineParametrization`	_xParametrization, _uniformParametrization, _chordalParametrization, _centripetalParametrization	`_splineParametrization = _uniformParametrization`
`_weights`	`Reals`	`(Reals w(10) ...) _weights=w`
`_spline`	`Spline`	`(BSpline bsc(points ...) _spline=bsc`

Important

Default value of _spline_BC is _clampedBC. With this condition, the spline is clamped at the end points and the tangential vectors are also prescribed. If you do not set the _tangent0 , _tangent1 parameters, tangent vectors will be chosen as \((1,0,0)\)! That means a 0 derivative at end points for C2 spline. The _tension parameter concerns only Catmull-Rom spline, its default value is 0.5 that provides curves realizing the best compromise (distance to the control points and curvatures).

These parameters are not available for any type of spline. They have default values regarding the type of spline, that are suitable to use splines with GMSH. If you are a newbie, do not play with spline parameters. For advanced users, read the section Splines for more details.

Important

By definition, the degree of a Bézier spline is equal to the number of control points minus one. XLiFE++ is compliant with this definition but GMSH is not. A Bézier curve in GMSH is a union of Bézier curves of degree 3 with several drawbacks : the curve is C0 but not necessary C1 and the number of points must be of the form \(3k+1\). So, to generate a mesh with GMSH , only Bézier spline of degree 3 with 4 control points are authorized. However, by using multiple Bézier curves of degree 3, it is possible by concatenating several SplineArc build from Bézier spline of degree 3.

To mesh the surface enclosed by the x-axis and and a spline approximation of the sinus curve, let define six points on the sinus curve

Number n=5;
std::vector<Point> points(n+1);
Real x=0, dx=pi_/n;
for(Number i=0;i<=n;i++, x+=dx) points[i]=Point(x,sin(x));

mesh using Catmull-Rom spline

Segment s(_v1=points[5], _v2=points[0], _hsteps=0.1, _domain_name="Sigma");
SplineArc sa(_splineType=_CatmullRomSpline, _vertices=points, _domain_name="Gamma",
             _hsteps=0.1);
Mesh msa(surfaceFrom(s+sa), _generator=gmsh);

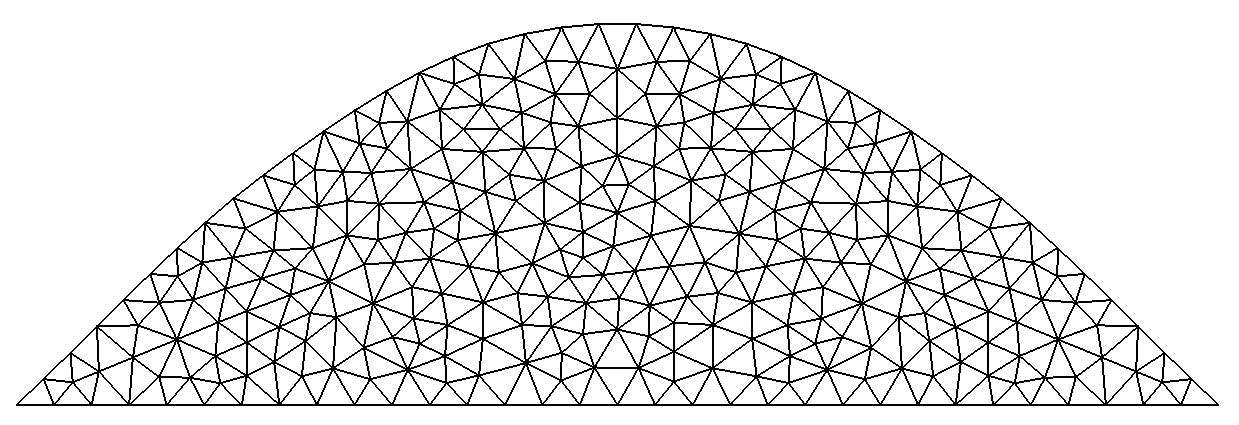
mesh using B-spline

Segment s(_v1=points[5],_v2=points[0],_hsteps=0.1,_domain_name="Sigma");
SplineArc sa(_splineType=_BSpline, _vertices=points, _domain_name="Gamma",
             _hsteps=0.1);
Mesh msa(surfaceFrom(s+sa), _generator=gmsh);

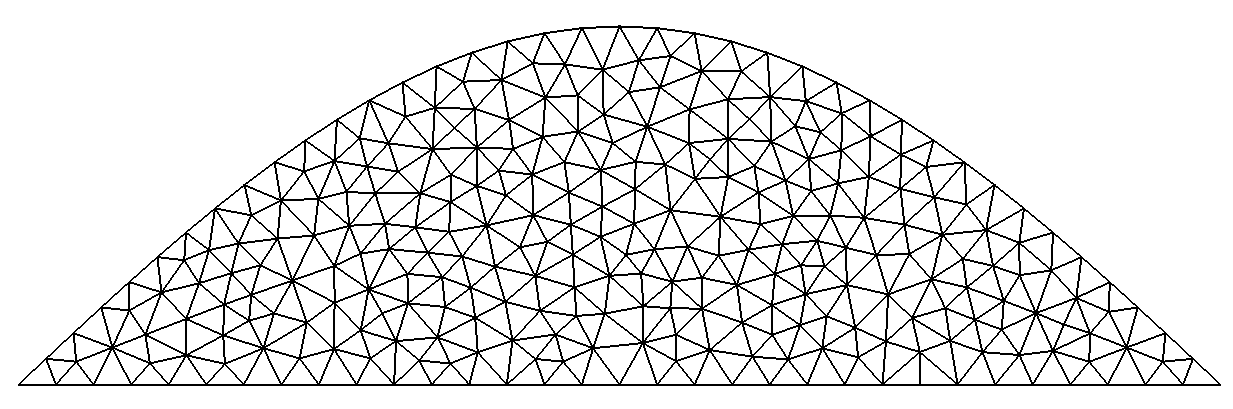
mesh using Bezier curve

As mentioned above, when GMSH is involved, only Bézier curve with 4 points are allowed:

n=3; points.resize(n+1);
x=0.;dx=pi_/n;
for(Number i=0;i<=n;i++, x+=dx) points[i]=Point(x,sin(x));
SplineArc sa(_splineType=_BezierSpline, _vertices=points, _domain_name="Gamma",
             _hsteps=0.1);
Mesh msa(surfaceFrom(s+sa), _generator=gmsh);

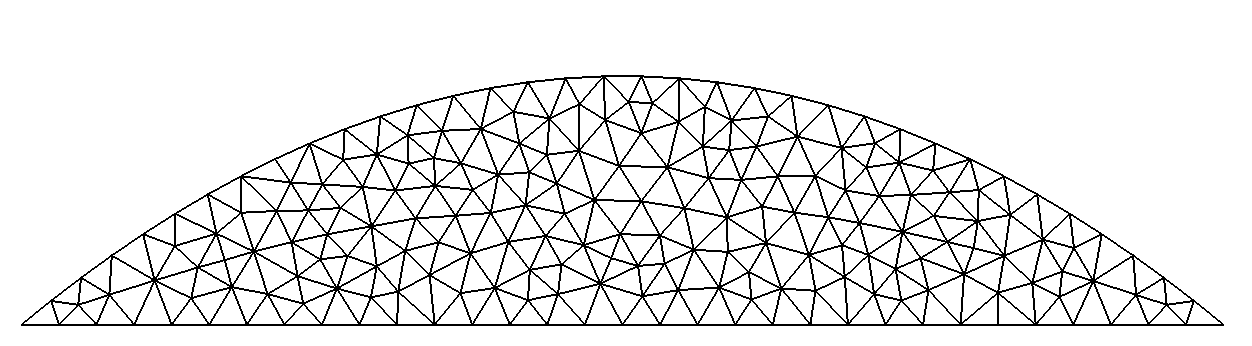
Obviously, Bézier approximation with 4 points is far away from the sinus curve!

To build a closed spline, it is sufficient to take the last control point same as the first control point. The following example show a closed Catmull-Rom spline built from 6 points located on an ellipse:

Number n=6;
vector<Point> pts(n+1);
Real s=0, ds=2*pi_/ns;
for(Number i=0;i<=n;i++,ss+=ds) pts[i]=Point(2*cos(s),sin(s));
SplineArc sd(_splineType=_CatmullRomSpline,_vertices=pts, _domain_name="Gamma",
             _hsteps=0.1);
Mesh msd(surfaceFrom(sd), _generator=gmsh);

Important

As splines are curves (1D objects) do not forget to construct the surface by invoking the surfaceFrom command.

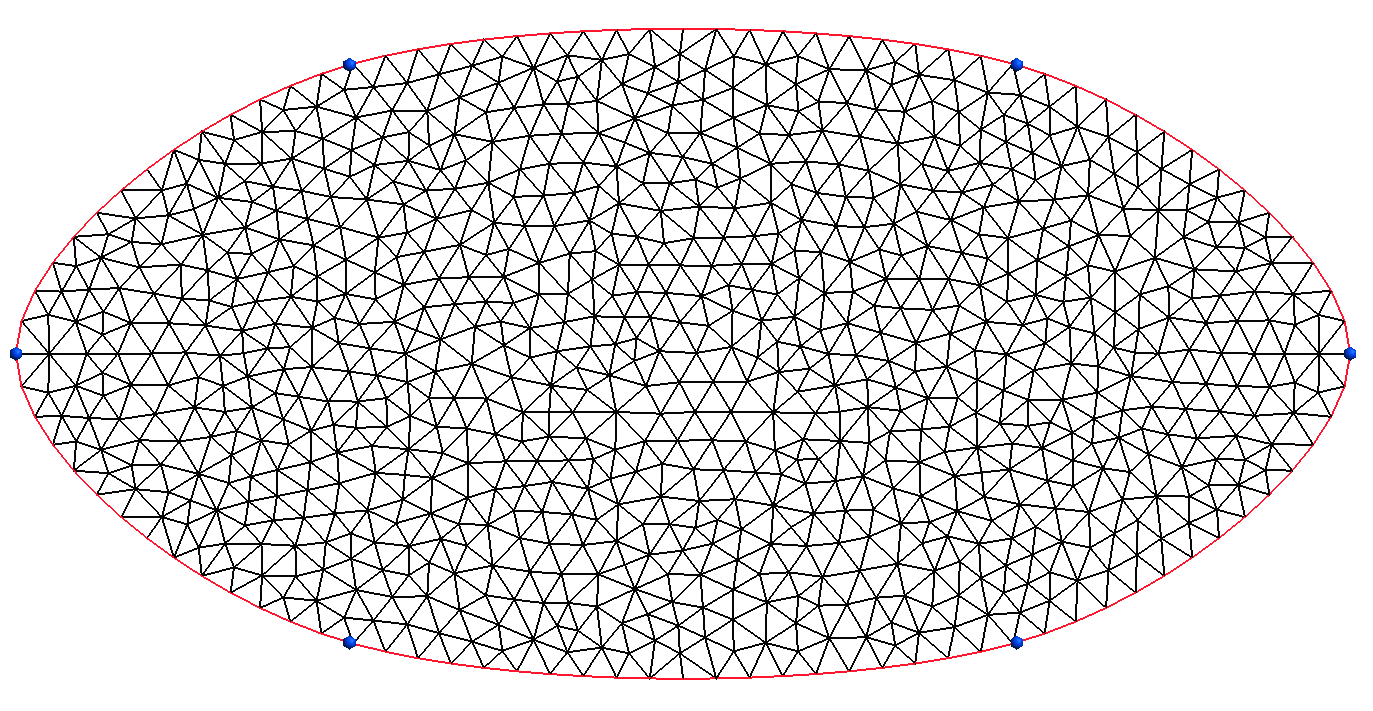
Note that users can access to the parametrization of a SplineArc and so on, to some particular quantities such as parameter bounds, curvature, curvilinear abscissa, normal vector, … (see the Parametrization class):

SplineArc sa(_splineType=_BSpline,_vertices=points,_hsteps=0.1);
const Parametrization& pa=sa.parametrization();
RealPair bs=pa.bounds();
Real tm=(bs.first+bs.second)/2;
theCout<<" bounds ="<<bs<<eol;
theCout<<"pa.curvature(tm) = "<<pa.curvature(tm)<<eol;
theCout<<"pa.curabc(tm) = "<<pa.curabc(tm)<<eol;
theCout<<"pa.normal(tm) = "<<pa.normal(tm)<<eol;
theCout<<"pa.tangent(tm) = "<<pa.tangent(tm)<<eol;

Hint

Parametrization of the spline arc is related to the Spline class parametrization (see Splines)

SplineArc#

`SplineArc`#