TermMatrix and TermVector in details

This library addresses the Term class and its inherited classes that handle the numerical representations of linear and bilinear forms involved in problems to be solved, say vectors and matrices (LargeMatrix class).

The Term class is an abstract class collecting general data (name, computing information) and has four children:

• TermVector class to represent linear forms involving multiple unknowns,

• SuTermVector class to represent linear forms involving only one unknown,

• TermMatrix to represent bilinear forms involving multiple pairs of unknowns,

• SuTermMatrix to represent bilinear forms involving only one pair of unknowns,

TermVector class is linked to a LinearForm object (defined on multiple unknowns) and handles a map of SuTermVector object indexed by unknown.

In a same way, TermMatrix class is linked to a BiLinearForm object (defined on multiple unknown pairs) and handles a map of SuTermMatrix object indexed by unknown pair. SuTermVector and SuTermMatrix are related to SuLinearForm and SuBiLinearForm and carries the numerical representations as vector or matrix. This is a block representation.

For instance, consider the following two unknowns \((u,p)\in V\times H\) problem:

\[\begin{split}\left\{ \begin{array}{lll} a(u,v)+b(p,v)&=&f(v)\\ c(u,q)+d(p,q)&=&g(q)\\ \end{array} \right.\end{split}\]

where \(a\), \(b\), \(c\), \(d\) are bilinear forms defines respectively on \(V\times V\), \(H\times V\), \(V\times H\), \(H\times H\) and \(f\), \(g\) are linear forms defined on \(V\) and \(H\). The block representation is

\[\begin{split}\left[\begin{array}{cc} \mathbb{A}&\mathbb{B}\\ \mathbb{C}&\mathbb{D}\\ \end{array} \right] \left(\begin{array}{c} U\\ P\\ \end{array} \right) = \left(\begin{array}{c} F\\ G\\ \end{array} \right)\end{split}\]

matrices being stored with their own storages. In order to shadow the type of coefficients (real, complex, scalar, vector, matrix) the vector and matrix representations are managed through the VectorEntry class (see utils library) and MatrixEntry class (see largeMatrix library).

In certain circumstances the block representation is not well adapted (matrix factorization, essential condition to apply). So the representation is moved to a scalar global representation, block representation may be or not kept.

This library collects the main algorithms of vector and matrix computation, in particular

• computation from linear and bilinear form (see the computation subdirectory)

• computation from explicit vector, matrix or function (nodal computation)

• linear combination of TermVector or TermMatrix (see LcTerm class)

• the elimination process due to essential conditions (in relation with essentialConditions library)

• the interface to solvers (direct solvers, iterative solvers or eigen solvers defined in largeMatrix, solvers, eigenSolvers libraries)

• some import and export facilities (see the ioTerms subdirectory)

Important

TermMatrix and TermVector are end user classes, therefore the functions that interact with users has to be simply designed!

The term class

The Term class is the abstract basis class of TermVector, TermMatrix, SuTermVector, SuTermMatrix classes. It collects general information:

class Term
{
 protected :
  String name_;                 //term name
  TermType termType_;           //type of term
  ComputingInfo computingInfo_; //computing information
 public :
  Parameters params;            //a free zone to store additional data
  static std::vector<Term *> theTerms;
}

where TermType enumerates the child types:

enum TermType {_termUndef,_termVector,_termMatrix,_sutermVector,_sutermMatrix};

and ComputingInfo collect various computing information:

class ComputingInfo
{
 public :
  bool isComputed;
  bool noAssembly;
  bool multithreading
  bool useGpu;
  StorageType storageType;           //_cs,_skyline,_dense
  AccessType storageAccess;          //_row,_col,_dual,_sym
  EliminationMethod elimination;     //_noElimination, _pseudoElimination, _realElimination
};

Using a static vector of Term pointers, the class maintains a list of all terms.

This class provides a default constructor, declared protected to forbid instantiation by user, and some basic functions (mainly accessors):

Term(const String& na="", ComputingInfo ci=ComputingInfo()); //protected
virtual ~Term();
const String& name() const;
String& name();
TermType termType() const;
TermType& termType();
ComputingInfo computingInfo() const;
ComputingInfo& computingInfo();
bool& computed();
bool computed() const;
virtual void compute()=0;
virtual void clear()=0;
virtual void print(std::ostream&) const=0;
friend std::ostream& operator<<(std::ostream&,const Term&);
static void clearGlobalVector();

Finally, some general functions (to compute and clear terms) are provided:

void compute(Term&);
void compute(Term&, Term&);
...
void clear(Term&);
void clear(Term&, Term&);
...

See also

• library=term,

• header=Term.hpp,

• implementation=Term.cpp,

• test=test_TermVector.cpp,

• header dep= essentialConditions.hpp, config.h, utils.h

The TermVector class

The TermVector class carries numerical representation of a linear form and more generally any vector attached to an approximation space:

class TermVector : public Term
{
  protected :
    LinearForm linForm_;
    map<const Unknown*, SuTermVector*> suTerms_;
    VectorEntry* entries_p;
    VectorEntry* scalar_entries_p;
    vector<DofComponent> cdofs_;
}

The linear form is a multiple unknowns form, may be reduced to a single unknown form (see form library). This linear form is void if TermVector is not explicitly construct from a linear form (linear combination, nodal construction). The map suTerms_ carries each vector block related to an unknown.

When there is only one element in map, it means that the TermVector is actually a single unknown term vector. The scalar_entries_p pointer may be allocated to concatenate the block vectors. When unknowns are vector unknowns, the representation may be not suited in certain cases (direct solver), so it is possible to create its scalar representation using the scalar_entries_p (VectorEntry pointer).

The VectorEntry object created has to be of real scalar or complex scalar type. In that case, a non block row numbering consisting in vector of DofComponent (Unknown pointer, dof number, component number) is also defined (cdofs_).

The TermVector class provides useful constructors and assign operators designed for end users :

//default constructor
TermVector(const String& na = "", bool noass = false);

//from linear form with options and no essential conditions
TermVector(const LinearForm&, const string_t& na="");
TermVector(const LinearForm&, TermOption, const string_t& na="");
TermVector(const LinearForm&, TermOption, TermOption, const string_t& na="");
TermVector(const LinearForm&, TermOption, TermOption, TermOption, const string_t& na="");

//from linear form with options and one essential condition
TermVector(const LinearForm&, const EssentialConditions&, const string_t& na="");
TermVector(const LinearForm&, const EssentialConditions&, TermOption, const string_t& na="");
TermVector(const LinearForm&, const EssentialConditions&, TermOption, TermOption, const string_t& na="");
TermVector(const LinearForm&, const EssentialConditions&, TermOption, TermOption, TermOption, const string_t& na="");

void build(const LinearForm &, const EssentialConditions*, const vector<TermOption>&, const string_t&);

// from value or function (interpolation)
template <typename T>
TermVector(const Unknown&, const Domain&, const T&, const String& na = "");

// copy like
TermVector(const TermVector&, const String& na = "");
template <typename T>
TermVector(const TermVector&, const T&, const String& na);
TermVector(const SuTermVector &, const String& na="");
TermVector(SuTermVector*, const String& na="");
void copy(const TermVector&, const String &);

// constructor from explicit function of TermVector's
TermVector(const TermVector&, funSR1_t& f, const string_t& na="");
TermVector(const TermVector&, TermVector&, funSR2_t& f, const string_t& na="");
TermVector(const TermVector&, funSC1_t& f, const string_t& na="");
TermVector(const TermVector&, TermVector&, funSC2_t& f, const string_t& na=""); single unknown

// constructor from symbolic function of TermVector's
TermVector(const TermVector&, const SymbolicFunction& , const string_t& na="");
TermVector(const TermVector&, const TermVector&, const SymbolicFunction& fs, const string_t& na="");
TermVector(const TermVector&, const TermVector&, const TermVector&, const SymbolicFunction& fs, const string_t& na="");

// constructor of a vector TermVector from scalar TermVector's (single unknown, same space)
TermVector(const Unknown&, const TermVector&, const TermVector&, const string_t& ="");
TermVector(const Unknown&, const TermVector&, const TermVector&, const TermVector&, const string_t& ="");
TermVector(const Unknown&, const TermVector&, const TermVector&, const TermVector&, const TermVector&, const string_t& ="");

// from linear combination
TermVector(const LcTerm&);
// assignment
TermVector& operator=(const TermVector&);
TermVector& operator=(const LcTerm&);
// insert SuTermVector in TermVector
void insert(const SuTermVector &);
void insert(SuTermVector*);
void insert(const Unknown*, SuTermVector*);
// destructor, clear
virtual ~TermVector();
void clear();

When TermVector is constructed from linear form, it is automatically computed except if it has set to be not computed using the TermOption _notCompute in its construction. TermOptions are managed as an enumeration:

enum TermOption
{
//general
_compute,                 // default behaviour
_notCompute,
_assembled,               // default behaviour
_unassembled,             // not yet available
//only for TermMatrix
_nonSymmetricMatrix,      // to force symmetry property
_symmetricMatrix,
_selfAdjointMatrix,
_skewSymmetricMatrix,
_skewAdjointMatrix,
_csRowStorage,            // to force storage
_csColStorage,
_csDualStorage,
_csSymStorage,
_denseRowStorage,
_denseColStorage,
_denseDualStorage,
_skylineSymStorage,
_skylineDualStorage,
_pseudoReduction,         // default behaviour
_realReduction,           // not yet available
_penalizationReduction    // not yet available
};

Constructors involving SuTermVector class are reserved to developers. End users should not have to acces to SuTermVector class, but we decide to let this access free to advanced users. Constructors involving LcTerm class are implicitly used by users when they write combination of terms in a symbolic way. The class provides some useful accessors (for users or developers):

//user accessors
const LinearForm& linearForm() const;
Number nbOfUnknowns() cons;
bool isSingleUnknown() const;
set<const Unknown*> unknowns() const;
ValueType valueType() const;
Number size() const;
Number nbDofs() const;
Number nbDofs(const Unknown&) const;
const vector<DofComponent>& cdofs() const;
vector<DofComponent>& cdofs(;
const Dof& dof(const Unknown&, Number ) const;

//developer accessors
cit_mustv begin() const;
it_mustv begin();
cit_mustv end() const;
it_mustv end();
SuTermVector* firstSut() const;
SuTermVector* firstSut();
const Unknown* unknown() const;
VectorEntry*& entries();
const VectorEntry* entries() const;
VectorEntry*& scalar_entries();
const VectorEntry* scalar_entries() const;
VectorEntry* actual_entries() const;

it_mustv and cit_mustv are iterator aliases:

typedef map<const Unknown*, SuTermVector*>::iterator it_mustv;
typedef map<const Unknown*, SuTermVector*>::const_iterator cit_mustv;

Access to a block of TermVector say a SuTermVector is proposed in two ways : either using subVector functions returning reference or pointer to SuTermVector objects or using operator() returning a new TermVector object, the SuTermVector object being copied. This last method is adressed to end users. For particular purpose, it is also possible to reinterpret a TermVector as a raw vector or a raw vector of vectors (say a Vector<S> or a Vector<Vector<S> > with S a Real or a Complex).

const SuTermVector& subVector() const;
SuTermVector& subVector(const Unknown*);
const SuTermVector& subVector(const Unknown*) const;
SuTermVector& subVector(const Unknown&);
const SuTermVector& subVector(const Unknown&) const;
SuTermVector* subVector_p(const Unknown*);
const SuTermVector* subVector_p(const Unknown*) const;
TermVector operator()(const Unknown&) const; //user usage
template<typename T>
Vector<T>& asVector(Vector<T>&) const;

The main computing operations are related to the construction of TermVector from linear form and construction from linear combination TermVector:

void compute();
void compute(const LcTerm&); // implicit
TermVector& operator+=(const TermVector&);
TermVector& operator-=(const TermVector&);
template<typename T>
TermVector& operator*=(const T&);
template<typename T>
TermVector& operator/=(const T&);

Note that the evaluation of TermVector defined by a value or a function is done during creation of TermVector. The algebraic operators +=, -=, *=, /= do the computation, it is not delayed as it is the case for +,``-,``* and / operators. The linear combination is based on LcTerm class which manages a list of pairs of Term and coefficient. Algebraic operators on TermVector produce LcTerm object carrying the linear combination that will be computed by TermVector constructor or assignment operator:

const TermVector& operator+(const TermVector&);
LcTerm operator-(const TermVector&);
LcTerm operator+(const TermVector&, const TermVector&);
LcTerm operator-(const TermVector&, const TermVector&);
LcTerm operator+(const LcTerm&, const TermVector&);
LcTerm operator-(const LcTerm&, const TermVector&);
LcTerm operator+(const TermVector&, const LcTerm&);
LcTerm operator-(const TermVector&, const LcTerm&);
template<typename T>
LcTerm operator*(const TermVector&, const T&);
template<typename T>
LcTerm operator*(const T&, const TermVector& )
template<typename T>
LcTerm operator/(const TermVector&, const T&)

To manage different representation of TermVector, the following function are provided :

void toScalar(bool keepEntries=false);
void toVector(bool keepEntries=false);
void toGlobal(bool keepSuTerms=false);
void toLocal(bool keepGlobal=false);
void adjustScalarEntries(const vector<DofComponent>&);

Note the difference between toScalar and toGlobal. toScalar forces the scalar representation of SuTermVector’s and toGlobal go to non block representation, allocating the scalar_entries_p pointer of TermVector. toGlobal operation induces toScalar operation. toLocal reconstructs block representation from global representation (inverse of toGlobal) and toVector returns to vector representation (inverse of toScalar).

In some circonstances, to avoid recomputation, it may be usefull to change the unknowns of a TermVector without changing its content, with an optional management of components of unknown:

void changeUnknown(const Unknown&, const Unknown&, const Vector<Number>& = Vector<Number>());
void changeUnknown(const Unknown&, const Vector<Number>& = Vector<Number>());
void changeUnknown(const Unknown&, Number);                 // shortcut
void changeUnknown(const Unknown&, Number, Number);         // shortcut
void changeUnknown(const Unknown&, Number, Number, Number); // shortcut

The principle of changeUnknown functions is the following :

• when two unknowns (u, v) are specified, the unknown u is replaced by the unknown v and the reference to unknown u does no longer exists in TermVector

• when a renumbering components vector (rc) is given too, components are re-settled along this vector

• when v is not specified, only components are re-settled

Here are some examples :

• u a scalar unknown, v a scalar unknown, replace unknown u by unknown v

• u a scalar unknown, v a 3-vector unknown, rc=[2] leads to sutv = [0 sutv 0]

• u a 4-vector unknown, v a 2-vector unknown, rc=[2,4] leads to sutv = [0 sutv1 0 sutv2]

• u a 3-vector unknown, rc=[3,0,1], re-settle components as [sutu3 0 sutu1]

Warning

Be cautious that there is no check of the space consistancy! So use it with care.

It is possible to adress values of a TermVector by unknown and index, to get it or to set it:

Value getValue(const Unknown&, Number) const;
void setValue(const Unknown&, Number, const Value&);
void setValue(const Unknown&, Number, const Real&);
void setValue(const Unknown&, Number, const Complex&);
void setValue(const Unknown&, Number, const vector<Real>&);
void setValue(const Unknown&, Number, const vector<Complex>&);

The Value class handles different type of values, in particular Real and Complex values. It is also possible to change some values of a TermVector by specifying the unknown that it is concerned, the geometrical part where values will be changed and the values that can be given either by a constant, a function or a TermVector:

Number dofRank(const Unknown&, const Dof&)const;
Number dofRank(const Dof&) const;
Value getValue(const Unknown&, Number) const;
Value getValue(const Unknown& u, const Dof& dof) const;
void setValue(const Unknown&, Number, const Value&);
void setValue(const Unknown& u, const Dof& dof, const Value& v);
void setValue(const Unknown&, Number, const Real&);
void setValue(const Unknown&, Number, const Complex&);
void setValue(const Unknown&, Number, const std::vector<Real>&);
void setValue(const Unknown&, Number, const std::vector<Complex>&);
template <typename T>
void setValue(const Unknown&, const GeomDomain&, const T&);
void setValue(const Unknown&, const GeomDomain&, const TermVector&);
void setValue(const Unknown&, const TermVector&);

In all setValue and getValue functions, the unknown may be omitted. In that case, the first unknown is assumed.

Most powerful functions are functions that can evaluate any function of approximation space (\(V_h\)) (representing by a TermVector U) at any point, using space interpolation:

\[u_h(x)= \sum_{i=1,n} U_{u,i}w_i(x)\]

where \(U_{u,i}\) is the \(i^{th}\) components related to the unknown \(u\) of TermVector \(U\) and \((w_i)_{i=1,n}\) the basis functions of approximation space \(V_h\).

Value evaluate(const Unknown&, const Point&) const;
template<typename T>
T& operator()(const vector<Real>&, T&) const;
template<typename T>
T& operator()(const Unknown&, const vector<Real>&, T&) const;

Some additional computational tools are available:

TermVector& toAbs();
TermVector& toReal();
TermVector& toImag();
TermVector& toComplex();
TermVector& toConj();
TermVector& roundToZero(Real aszero=10*theEpsilon);
Real norm2() const;
Complex maxValAbs() const;

TermVector may be related to essential conditions either by defining an essential condition from a TermVector (e.g u=TU) or by applying some essential conditions (SetOfConstraints or EssentialConditiopns objects) to it:

EssentialCondition operator = (const Complex &);
TermVector& applyEssentialConditions(const SetOfConstraints& soc, const ReductionMethod& rm=ReductionMethod());
TermVector& applyEssentialConditions(const EssentialConditions& ecs, const ReductionMethod& rm=ReductionMethod());
TermVector& applyBoundaryConditions(const EssentialConditions& ecs, const ReductionMethod& rm=ReductionMethod());

In order to use a TermVector as an interpolated function, the toFunction() builds a new function where the TermVector is passed to the Parameters of some particular functions that implements the interpolation:

const Function& toFunction() const;
Real fun_EC_SR(const Point& P, Parameters& pars);
Real fun_EC_SC(const Point& P, Parameters& pars);
Real fun_EC_VR(const Point& P, Parameters& pars);
Real fun_EC_VC(const Point& P, Parameters& pars);

The following functions produce new TermVector’s that are defined on another domain, one mapping the values using a predefined map between two domains the other restricting the values to one domain (included in the current one):

TermVector mapTo(const GeomDomain&, const Unknown&, bool errOutDom =true) const;
TermVector onDomain(const GeomDomain&) const;

The class proposes some basic output functions:

void print(ostream&) const;
void saveToFile(const String&, bool encode=false) const;

Besides, some of the functionalities are also provided as extern functions:

//linear combination
const TermVector& operator+(const TermVector&);
LcTerm operator-(const TermVector&);
LcTerm operator+(const TermVector&, const TermVector&);
LcTerm operator-(const TermVector&, const TermVector&);
LcTerm operator+(const LcTerm&, const TermVector&);
LcTerm operator-(const LcTerm&, const TermVector&);
LcTerm operator+(const TermVector&, const LcTerm&);
LcTerm operator-(const TermVector&, const LcTerm&);
template<typename T> LcTerm operator*(const TermVector&, const T&);
template<typename T> LcTerm operator*(const T&, const TermVector&);
template<typename T> LcTerm operator/(const TermVector&, const T&)

//inner, hermitian product, norm, ...
TermVector abs(const TermVector&);
TermVector real(const TermVector&);
TermVector imag(const TermVector&);
TermVector conj(const TermVector&);
Complex innerProduct(const TermVector&, const TermVector&);
Complex hermitianProduct(const TermVector&, const TermVector&);
Complex operator|(const TermVector&, const TermVector&);
Real norm(const TermVector&, Number l=2);
Real norm1(const TermVector&);
Real norm2(const TermVector&);
Real norminfty(const TermVector&);

//output functions
void print(ostream&) const;
void saveToFile(const String&, bool encode=false) const;
void saveToFile(const String&, const list<const TermVector*>&, IOFormat iof=_raw);
void saveToFile(const String&, const TermVector&, IOFormat iof=_raw);
void saveToFile(const String&, const TermVector&, const TermVector&, IOFormat iof=_raw);
void saveToFile(const String&, const TermVector&, const TermVector&, const TermVector&, IOFormat iof=_raw);
void saveToFile(const String&, const TermVector&, const TermVector&, const TermVector&, const TermVector&, IOFormat iof=_raw);

Available export format are

• _raw : export only the values in a raw format

• _vtu : export mesh and values displayable with Paraview

• _matlab : export mesh and values as an executable Matlab file

• _xyzv: export mesh nodes and values as x y z v1 v2 …

Integral represention is a particular operation mixing numerical quadrature and interpolation :

\[u(x_i)=\int_{\Gamma} opk(K)(x_i,y)\, aop\, opu(p)(y)dy\ \ i=1,n.\]

where \(K\) is a kernel, \(opk\) an operator on kernel (OperatorOnKernel), \(p\) a layer potential, \(opu\) an operator on unknown (OperatorOnUnknown) and \(aop\) an algebraic operator.

template<typename T>
Vector<T>& integralRepresentation(const vector<Point>& xs, const LinearForm& lf, const TermVector& U, Vector<T>& val);
TermVector integralRepresentation(const Unknown&, const GeomDomain&, const LinearForm&, const TermVector&);

For instance, the single layer integral representation on a list of points is computed as follows:

Vector<Point>Points;
...
Vector<Real> val;
integralRepresentation(Points, intg(gamma, G(_y) * u), U, val);

or if the list of points is the list of nodes of a domain:

TermVector IR=integralRepresentation(Omega, intg(gamma, G(_y) * u), U, val);

For most of the functions of TermVector, the algorithms travel the map of SuTermVector, calling SuTermVector ‘s functions. For instance, the compute function looks like:

void TermVector::compute()
{
  for(it_mustv it = suTerms_.begin(); it != suTerms_.end(); it++)
  {
    if (!it->second->computed()) it->second->compute();
  }
  computed() = true;
}

See also

TermVector infos:

• library=term

• header=TermVector.hpp,

• implementation=TermVector.cpp,

• test=test_TermVector.cpp,

• header dep=SuTermVector.hpp, termUtils.hpp, Term.hpp, form.h, config.h, utils.h

The SuTermVector class

The SuTermVector class carries numerical representation of a single linear form and more generally any vector attached to an approximation space.

class SuTermVector : public Term
{
 protected :
    SuLinearForm* sulf_p;
    const Unknown* u_p;
    mutable Space* space_p;
    std::vector<Space*> subspaces;
    VectorEntry* entries_p;
    VectorEntry* scalar_entries_p;
    std::vector<DofComponent> cDoFs_;
}

The sulf_p contains a pointer to a SuLinearForm (single unknown linear form). It may be null, that means there is no explicit linear form attached to the SuTermVector.

The space_p pointer points to the largest subspace involved in SuTermVector. This pointer should not be null because it carries the DoFs numbering of vector. For this reason too, the largest subspace has to be correctly updated during any operation on SuTermVector.

The Space vector subspaces contains the subspaces (as subspace of the largest space) attached to basic linear forms defined in the SuLinearForm pointer (if defined), see buildSubspaces() function.

Warning

Do not confuse the space_p pointer and u_p->space_p pointer that specifies the whole space. They may be the same!

The numerical representation of vector is defined in the entries_p VectorEntry pointer as a real/complex vector or a real/complex vector of vectors, regarding the value type (real or complex) and the structure of the unknown (scalar or vector). If required, vector of vectors representation may be expanded to a vector of scalars stored in the scalar_entries_p VectorEntry pointer. In that case the cDoFs_ vector of DofComponent gives the numbering (in DofComponent) of entries. Note that if SuTermVector is of scalar type, scalar_entries_p = entries_p.

The SuTermVector class provides one constructor from linear form, some constructors from constant value, functions or symbolic functions, one constructor from linear combination and some copy constructors:

//constructor from linear form
SuTermVector(SuLinearForm* sulf = 0, const String& na = "", bool noass = false);
//constructors from constant value or function (no linear form)
SuTermVector(const String&, const Unknown*, Space*, ValueType vt = _real, Number n = 0, Dimen nv = 0, bool noass = false); //vector of zeros
template <typename T>
 SuTermVector(const Unknown&, const GeomDomain&, const Vector<T>&, const String&, bool);
template <typename T>
 SuTermVector(const Unknown&, const GeomDomain&, const T&, const String&, bool);
 SuTermVector(const Unknown&, const GeomDomain&, funSR_t&, const String& na="", bool noass=false);
 SuTermVector(const Unknown&, const GeomDomain&, funSC_t&, const String& na="", bool noass =false);
 SuTermVector(const Unknown&, const GeomDomain&, funVR_t&, const String& na="", bool noass =false);
 SuTermVector(const Unknown&, const GeomDomain&, funVC_t&, const String& na="", bool noass =false);
 //constructor from explicit function of SuTermVector's
 SuTermVector(const SuTermVector&, funSR1_t& f, const string_t& na="");
 SuTermVector(const SuTermVector&, const SuTermVector&, funSR2_t& f, const string_t& na="");
 SuTermVector(const SuTermVector&, funSC1_t& f, const string_t& na="");
 SuTermVector(const SuTermVector&, const SuTermVector&, funSC2_t& f, const string_t& na="");
 //constructor from symbolic function of SuTermVector's
 SuTermVector(const SuTermVector&, const SymbolicFunction& , const string_t& na="");
 SuTermVector(const SuTermVector&, const SuTermVector&, const SymbolicFunction&, const string_t& na="");
 SuTermVector(const SuTermVector&, const SuTermVector&, const SuTermVector&, const SymbolicFunction&, const string_t& na="");
 //constructor of a vector SuTermVector from scalar SutermVector's
 SuTermVector(const Unknown&, const SuTermVector&, const SuTermVector&, const string_t& ="");
 SuTermVector(const Unknown&, const std::list<const SuTermVector*>&, const string_t& ="");
 //constructor from linear combination (no linear form)
 SuTermVector(const LcTerm&);
 //copy constructors and assign operator
 SuTermVector(const SuTermVector&);
 template<typename T>
  SuTermVector(const SuTermVector&, const T&);
 SuTermVector& operator=(const SuTermVector&);
 //other useful stuff
 virtual ~SuTermVector();
 void copy(const SuTermVector&);    //full copy
 void initFromFunction(const Unknown&, const GeomDomain&, const Function&, const String& na="", bool noass=false);
 void clear();

A lot of useful accessors and shortcuts to some properties are proposed:

string_t name();
void name(const string_t&);
SuLinearForm* sulfp() const;
SuLinearForm*& sulfp();
VectorEntry*& entries();
const VectorEntry* entries() const;
TermType termType() const;
ValueType valueType() const;
StrucType strucType() const;
const Unknown* up() const;
const Unknown*& up();
number_t nbOfComponents() const;
const Space* spacep() const;
Space*& spacep();
set<const Space*> unknownSpaces() const;
number_t nbDofs() const;
number_t size() const;
VectorEntry*& scalar_entries();
const VectorEntry* scalar_entries() const;
VectorEntry* actual_entries() const;
const vector<DofComponent>& cDoFs() const;
vector<DofComponent>& cDoFs();
const Dof& DoF(number_t n) const;
const GeomDomain* domain() const;

SuTermVector may be modified by the following operators and functions:

SuTermVector& operator+=(const SuTermVector&);
SuTermVector& operator-=(const SuTermVector&);
template<typename T>
 SuTermVector& operator*=(const T&);
template<typename T>
 SuTermVector& operator/=(const T&);
SuTermVector& merge(const SuTermVector&);
SuTermVector& toAbs();
SuTermVector& toReal();
SuTermVector& toImag();
SuTermVector operator()(const ComponentOfUnknown&) const;
SuTermVector& toComplex();
complex_t maxValAbs() const;
void setValue(number_t, const Value&);
void setValue(const Value&, const GeomDomain&);
void setValue(const Function&, const GeomDomain&);
void setValue(const SuTermVector&, const GeomDomain&);
void setValue(const SuTermVector&);

The operator () extracts unknown component term vector as a SuTermVector when Unknown is a vector unknown. For instance if u is a vector unknown, T(u[2]) returns a SuTermVector containing the elements of T corresponding to second component.

Some values can be extracted or computed from:

Value getValue(number_t) const;
SuTermVector* onDomain(const GeomDomain& dom) const;
template<typename T>
 T& operator()(const vector<real_t>&, T&) const;
SuTermVector* interpolate(const Unknown&, const GeomDomain&);
Value evaluate(const Point&) const;
template<typename T>
 Vector<T>& asVector(Vector<T>&) const;

SuTermVector provides real computation algorithms, in particular FE computation ones:

void buildSubspaces();
void compute();                 //!< compute from linear form
void compute(const LcTerm&);
template<typename T, typename K>
 void computeFE(const SuLinearForm&, Vector<T>&, K&);
template<typename T, typename K>
 void computeIR(const SuLinearForm&, Vector<T>&, K& vt, const vector<Point>&, const Vector<T>&, const vector<Vector<real_t> >* nxs=0);

Some particular member functions allow to change the internal representation:

void toScalar(bool keepVector=false);
void toVector(bool keepEntries=false);
void extendTo(const SuTermVector&);
void extendTo(const Space&);
void extendScalarTo(const vector<DofComponent>&, bool useDual = false);
SuTermVector* mapTo(const GeomDomain&, const Unknown&, bool =true) const;
void changeUnknown(const Unknown&, const Vector<number_t>&);
void adjustScalarEntries(const vector<DofComponent>&);

Some external function are provided to compute norms, …

Complex innerProduct(const SuTermVector&, const SuTermVector&);
Complex hermitianProduct(const SuTermVector&, const SuTermVector&);
Real norm1(const SuTermVector&);
Real norm2(const SuTermVector&);
Real norminfty(const SuTermVector&);

Finally, there are some print and export stuff:

void print(ostream&) const;
void print(ostream&, bool r, bool h) const; // raw and header option
void saveToFile(const String&, bool encode=false) const;

//extern save functions
void saveToFile(const string_t&, const Space*, const list<SuTermVector*>&, IOFormat iof=_raw, bool withDomName=true);
void saveToMsh(ostream&, const Space*, const list<SuTermVector*>&, vector<Point>, splitvec_t, const GeomDomain*);
void saveToMtlb(ostream&, const Space*, const list<SuTermVector*>&, vector<Point>, splitvec_t, const GeomDomain*);
void saveToVtk(ostream&, const Space*, const list<SuTermVector*>&,   vector<Point>,splitvec_t, const GeomDomain*);
void saveToVtkVtu(ostream&, const Space*, const list<SuTermVector*>&, vector<Point>, splitvec_t, const GeomDomain*);
pair<vector<Point>, map<number_t, number_t> > ioPoints(const Space* sp);
splitvec_t ioElementsBySplitting(const Space*, map<number_t, number_t>);

See also

• library=term,

• header=SuTermVector.hpp,

• implementation=SuTermVector.cpp,

• test=test_TermVector.cpp,

• header dep= Term.hpp, LcTerm.hpp, termUtils.hpp, config.h, utils.h

The TermVectors class

The TermVectors is simply an encapsulation of a list of TermVector. It implements a small interface to vector<TermVector> and it is adressed to beginners.

class TermVectors: public std::vector<TermVector>
{
  public :
    TermVectors(Number n=0);
    TermVectors(const std::vector<TermVector>& vs);
    const TermVector& operator()(Number n) const;
    TermVector& operator()(Number n);
    void print(std::ostream&) const;
};
std::ostream& operator<<(std::ostream&, const TermVectors&);

See also

TermVectors infos:

• library=term,

• header=TermVector.hpp,

• implementation=TermVector.cpp,

• test=test_TermVector.cpp,

• header dep=Term.hpp, LcTerm.hpp, termUtils.hpp, form.h, config.h, utils.h

The KernelOperatorOnTermVector class

To deal with integral representation, say for instance

\[v(x) = \int_{\Gamma}K(x,y)\,\varphi(y)\]

where \(\varphi\) will be represented by a TermVector object F, the user can define the linear form

\[\int_{\Gamma}K(x,y)\,u(y)\]

and then call the integralRepresentation() function to link its TermVector object F to the linear form. To make the user life easier, XLiFE++ provides a small class KernelOperatorOnTermVector that relates a OperatorOnKernel and a TermVector. So, writing intg(gamma, K*F) will be interpreted as the linear form acting to the TermVector F by handling in the back a KernelOperatorOnTermVector:

class KernelOperatorOnTermvector
{
 protected:
  OperatorOnKernel opker_; //Kernel operator
  AlgebraicOperator aop_;  //operation (*,|,%,^) between kernel and TermVector
  const TermVector*  tv_;  //TermVector involved
 public:
  bool termAtLeft;         //if true : opker aop tv else :  tv aop opker
}

The class provides one basic constructor and some accessors:

KernelOperatorOnTermvector(const OperatorOnKernel&, AlgebraicOperator, const TermVector&, bool atleft);
AlgebraicOperator algop();
AlgebraicOperator& algop();
const OperatorOnKernel& opker() const;
const TermVector*  termVector();
ValueType valueType() const;
bool xnormalRequired() const;
bool ynormalRequired() const;

Besides, external functions to the class manage the various operations involving Kernel and TermVector:

KernelOperatorOnTermvector operator*(const TermVector&, const Kernel&);
KernelOperatorOnTermvector operator|(const TermVector&, const Kernel&);
KernelOperatorOnTermvector operator^(const TermVector&, const Kernel&);
KernelOperatorOnTermvector operator%(const TermVector&, const Kernel&);
KernelOperatorOnTermvector operator*(const Kernel&, const TermVector&);
...
KernelOperatorOnTermvector operator*(const TermVector&, const OperatorOnKernel&);
...
KernelOperatorOnTermvector operator*(const OperatorOnKernel&, const TermVector&);
...
OperatorOnUnknown toOperatorOnUnknown(const KernelOperatorOnTermvector&);

Finally, to build integral involving KernelOperatorOnTermvector some pseudo-constructors are provided

std::pair<LinearForm,const TermVector*>
intg(const GeomDomain&, const KernelOperatorOnTermvector&,const IntegrationMethod&);
std::pair<LinearForm,const TermVector*>
intg(const GeomDomain&, const KernelOperatorOnTermvector&,const IntegrationMethods&);
std::pair<LinearForm,const TermVector*>
intg(const GeomDomain&, const KernelOperatorOnTermvector&,QuadRule = _defaultRule, number_t =0);

See also

• library=term,

• header=KernelOperatorOnTermVector.hpp,

• implementation=KernelOperatorOnTermVector.cpp,

• test=test_operator.cpp,

• header dep= OperatorOnKernel.hpp, TermVector.hpp, config.h, utils.h

The TermMatrix class

The TermMatrix class carries numerical representation of a bilinear form and more generally any matrix attached to a pair of unknowns. It follows a similar organization to TermVector class but manages row and column information:

class TermMatrix : public Term
{
  protected :
  BilinearForm bilinForm_;              // bilinear form if exists
  map<uvPair, SuTermMatrix*> suTerms_;  // list of SuTermMatrix
  MatrixEntry* scalar_entries_p;        // scalar entries representation
  vector<DofComponent> cdofs_c;         // column scalar dofs
  vector<DofComponent> cdofs_r;         // row scalar dofs
  SetOfConstraints* constraints_u_p;    // constraints to apply to row
  SetOfConstraints* constraints_v_p;    // constraints to apply to column
  MatrixEntry* rhs_matrix_p;            // matrix used by right-hand side correction
}

The bilinear form is a multiple unknown pairs form, may be reduced to a single unknown pair form (see form library). This bilinear form is void if TermMatrix is not explicitly construct from a bilinear form (linear combination, nodal construction, …). In particular, this bilinear form is not updated when TermMatrix objects are combined. The map suTerms_ carries each matrix block related to a pair of unknowns. When there is only one element in map, it means that the TermMatrix is actually a single unknown pair term matrix.

As block representation may be too restrictive in certain cases, it is possible to create its non block representation in scalar_entries_p (MatrixEntry pointer). The MatrixEntry object created has to be of real scalar or complex scalar type. In that case, non block row and non block column numbering, consisting in vectors of DofComponent (Unknown pointer, dof number, component number), are also defined (cdofs_r and cdofs_c).

Essential conditions (conditions on space functions) induce special treatments in computation of TermMatrix. It is the reason why they are handled with SetOfConstraints objects which are the algebraic representations of essential conditions (see essentialConditions for details). SetOfConstraints on row may differ from SetOfConstraints on column (it is often the same). In case of non homogeneous essential condition, the part of matrix that is eliminated contributes to the right hand side; this part is stored into rhs_matrix_p MatrixEntry pointer. Obviously, the pointers constraints_u_p, constraints_v_p, rhs_matrix_p are null pointer whenever no essential conditions are imposed.

The TermMatrix class provides useful constructors and assign operators designed for end users :

TermMatrix(const String & na="?");

//constructors with no essential boundary conditions and options
TermMatrix(const BilinearForm&, const String& na="");
TermMatrix(const BilinearForm&, TermOption, const String& na="");
TermMatrix(const BilinearForm&, TermOption, TermOption, const String& na="");
...
//constructor with one essential boundary condition (on u and v)
TermMatrix(const BilinearForm&, const EssentialConditions&, const String& na="");
TermMatrix(const BilinearForm&, const EssentialConditions&, TermOption, const String& na="");
...
//constructor with one essential boundary condition and explicit reduction method
TermMatrix(const BilinearForm&, const EssentialConditions&, const ReductionMethod&, const String& na="");
TermMatrix(const BilinearForm&, const EssentialConditions&, const ReductionMethod&, TermOption, const String& na="");
...
//constructor with  two essential boundary conditions (on u and v)
TermMatrix(const BilinearForm&, const EssentialConditions&, const EssentialConditions&, const String& na="");
TermMatrix(const BilinearForm&, const EssentialConditions&, const EssentialConditions&, TermOption, const String& na="");
...
//constructor with two essential boundary conditions and explicit reduction method
TermMatrix(const BilinearForm&, const EssentialConditions&, const EssentialConditions&, const ReductionMethod&, const String& na="");
TermMatrix(const BilinearForm&, const EssentialConditions&, const EssentialConditions&, const ReductionMethod&, TermOption, const String& na="");
...
//effective constructor
void build(const BilinearForm& blf, const EssentialConditions* ecu, const EssentialConditions* ecv, const vector<TermOption>&, const String& na);

//copy constructors
TermMatrix(const TermMatrix &, const String& na="");
// diagonal TermMatrix from a TermVector or a vector
TermMatrix(const TermVector &, const String& na="");
template<typename T> TermMatrix(const Unknown&, const GeomDomain&, const Vector<T> &, const String& na="");
//TermMatrix from a SuTermMatrix
TermMatrix(const SuTermMatrix &, const String& na=""); // full copy
TermMatrix(SuTermMatrix *, const String& na="");       // pointer copy
//TermMatrix of the form opker(xi,yj)
TermMatrix(const Unknown&, const GeomDomain&, const Unknown&, const GeomDomain&, const OperatorOnKernel&, const String& na="");
//TermMatrix from a row dense matrix (Matrix)
TermMatrix(const Matrix<T>& mat, const String& ="");
TermMatrix(const vector<T>& mat, Number m, Number n=0, const String& ="");
void buildFromRowDenseMatrix(const vector<T>&, Number, Number, const String&);
// TermMatrix from a linear combination
TermMatrix(const LcTerm&,const String& na="");

//assign operator
TermMatrix& operator=(const TermMatrix&);
TermMatrix& operator=(const LcTerm&);

The ReductionMethod class allows the user to specify the reduction method he wants, one of the enumeration ReductionMethodType: _pseudoReduction, _realReduction, _penalizationReduction, _dualReduction. It is also possible to provide an additional real/complex parameter (say alpha): the diagonal coefficient of the pseudo-eliminated part or the penalization coefficient.

ReductionMethodType method; // type of reduction method
Complex alpha;              // diagonal or penalization coefficient
ReductionMethod(ReductionMethodType= _noReduction, const Complex& = 1.);
void print(ostream& out) const;
friend :ostream& operator << (ostream&, const ReductionMethod&);

Hint

When reduction method is not specified, the pseudo reduction with 1 as diagonal coefficient is used. ( Only the pseudo reduction method is available! )

Hint

When TermMatrix is constructed, it is automatically computed except if it has been set not to be computed, using the TermOption _notCompute in its construction.

Developers may use other construction/destruction stuff:

void initFromBlf(const BilinearForm &, const String& na ="", bool noass = false);
void initTermVector(TermVector&, ValueType, bool col=true);
template<typename T> void initTermVectorT(TermVector&, const T&, bool col=true);
void insert(const SuTermMatrix &);
void insert(SuTermMatrix *);
void copy(const TermMatrix&);
void clear();
virtual ~TermMatrix();

This class provides a lot of accessors and properties (shorcuts to other class accessors):

bool isSingleUnknown() const;
set<const Unknown*> rowUnknowns() const;
set<const Unknown*> colUnknowns() const;
Number nbTerms() const;
ValueType valueType() const;
AccessType storageAccess() const;
void setStorage(StorageType, AccessType);
StorageType storageType() const
bool hasConstraints() const;
FactorizationType factorization() const;
SymType globalSymmetry() const;
TermMatrix operator()(const Unknown&, const Unknown&) const;

//stuff reserved to developers
cit_mustm begin() const;
it_mustm begin();
cit_mustm end() const;
it_mustm end();
map<uvPair, SuTermMatrix*>& suTerms();
MatrixEntry*& scalar_entries();
const MatrixEntry* scalar_entries() const;
MatrixEntry*& rhs_matrix();
const MatrixEntry* rhs_matrix() const;
const vector<DofComponent>& cdofsr() const;
const vector<DofComponent>& cdofsc() const;
vector<DofComponent>& cdofsr();
vector<DofComponent>& cdofsc();
SuTermMatrix& subMatrix(const Unknown*, const Unknown*);
const SuTermMatrix& subMatrix(const Unknown*, const Unknown*) const;
SuTermMatrix* subMatrix_p(const Unknown*, const Unknown*);
const SuTermMatrix* subMatrix_p(const Unknown*, const Unknown*) const;

TermVector& getRowCol(Number, AccessType, TermVector&) const;
TermVector row(Number) const;
TermVector column(Number) const;
template <typename T>
LargeMatrix<T>& getLargeMatrix(StrucType =_undefStrucType) const;
template <typename T>
HMatrix<T,FeDof>& getHMatrix(StrucType =_undefStrucType) const;

Hint

The access operator() returns a SuTermMatrix as a TermMatrix (obviously a single unknown one). Note that it is a full copy. To avoid copy, use subMatrix member functions.

it_mustm and cit_mustm are iterator aliases:

typedef map<uvPair, SuTermMatrix*>::iterator it_mustm;
typedef map<uvPair, SuTermMatrix*>::const_iterator cit_mustm;

It is also possible to get row or column (index starts from 1) of the TermMatrix if it is a single unknown one and to access to the LargeMatrix or the HMatrix object that really stores the matrix values:

TermVector& getRowCol(Number, AccessType, TermVector&) const;
TermVector row(Number) const;
TermVector column(Number) const;
template <typename T> LargeMatrix<T>& getLargeMatrix(StrucType =_undefStrucType) const;
template <typename T> HMatrix<T,FeDof>& getHMatrix(StrucType =_undefStrucType) const;

Hint

The setStorage() function allows the user to impose the matrix storage.

The class proposes to users interfaces to computation algorithms (FE computation and algebraic operations):

void compute();
void compute(const LcTerm&, const String& na="");

template<typename T> TermMatrix& operator*=(const T&);
template<typename T> TermMatrix& operator/=(const T&);
TermMatrix& operator+=(const TermMatrix&);
TermMatrix& operator-=(const TermMatrix&);
friend TermVector& multMatrixVector(const TermMatrix&, const TermVector&, TermVector&);
friend TermVector& multVectorMatrix(const TermMatrix&, const TermVector&, TermVector&);
friend TermVector operator*(const TermMatrix&, const TermVector&);
friend TermVector operator*(const TermVector&, const TermMatrix&);
friend TermMatrix operator*(const TermMatrix&, const TermMatrix&);

The computation of TermMatrix is a quite intricate process in case of essential conditions to apply to bilinear form. The implementation of compute() looks like (some details are omitted):

void TermMatrix::compute()
{
    //compute suterms
    for(it_mustm it = suTerms_.begin(); it != suTerms_.end(); it++)
    it->second->compute();
    if(constraints_u_p==0 && constraints_v_p==0) {computed() = true; return;}
    //deal with essential conditions
    bool global=false;
    if(constraints_u_p!=0) global=constraints_u_p->isGlobal();
    if(constraints_v_p!=0 && !global) global=constraints_u_p->isGlobal();
    if(global) toGlobal(_noStorage, _noAccess, _noSymmetry, false);
    else toScalar();
    switch(computingInfo_.elimination)
    {
      case _noElimination: break;
      case _pseudoElimination: pseudoElimination(); break;
    }
    computed() = true;
}

The principle of pseudo-elimination consists in combining some rows and columns, and “eliminating” some rows and columns (in fact set to 0 except diagonal coefficient). Two cases are to be considered:

• case of essential conditions which do not couple unknowns

• case of essential conditions which couples unknowns (global constraints)

In the first case, the pseudo-elimination process may be performed on each matrix of SuTermMatrix involving unknowns concerned by essential conditions whereas in the second case, the process must be performed and the whole matrix of TermMatrix. If no such representation exists, we have to create it (toGlobal function). See the pseudoElimination() function.

This class offers many interfaces to factorization tools and direct solvers:

//developers stuff
void initTermVector(TermVector&, ValueType, bool col=true);
template<typename T>
void initTermVectorT(TermVector&, const T&, bool col=true);

void toScalar(bool keepEntries=false);
void toGlobal(StorageType, AccessType, SymType=_noSymmetry, bool keepSuTerms=false);
void toSkyline();
void mergeNumbering(map<const Unknown*, list<SuTermMatrix* > >&, map<SuTermMatrix*, vector<Number > >&, vector<DofComponent>&, AccessType);
void addIndices(vector<set<Number> >&, MatrixStorage*, const vector<Number>&, const vector<Number>&);
void mergeBlocks();
friend TermVector prepareLinearSystem(TermMatrix&, TermVector&, MatrixEntry*&, VectorEntry*&, bool toScal=false);
void pseudoElimination();

//direct solver member functions
void ldltSolve(const TermVector&, TermVector&);
void ldlstarSolve(const TermVector&, TermVector&);
void luSolve(const TermVector&, TermVector&);
void umfpackSolve(const TermVector&, TermVector&);
void sorSolve(const TermVector& V, TermVector& R, const Real w, SorSolverType sType);
void sorUpperSolve(const TermVector& V, TermVector& R, const Real w);
void sorDiagonalMatrixVector(const TermVector& V, TermVector& R, const Real w);
void sorLowerSolve(const TermVector& V, TermVector& R, const Real w);
void sorDiagonalSolve(const TermVector& V, TermVector& R, const Real w);

And users have to use the following external functions:

//factorization tool
void ldltFactorize(TermMatrix&, TermMatrix&);
void ldlstarFactorize(TermMatrix&, TermMatrix&);
void luFactorize(TermMatrix&, TermMatrix&);
void umfpackFactorize(TermMatrix&, TermMatrix&);
void factorize(TermMatrix&, TermMatrix&, FactorizationType ft=_noFactorization);

//direct solver (one right-hand side)
TermVector factSolve(TermMatrix&, const TermVector&);
TermVector ldltSolve(TermMatrix&, const TermVector&);
TermVector ldlstarSolve(TermMatrix&, const TermVector&);
TermVector luSolve(TermMatrix&, const TermVector&);
TermVector gaussSolve(TermMatrix&, const TermVector&, bool keepA = false);
TermVector umfpackSolve(TermMatrix&, const TermVector&, bool keepA = false);
TermVector magmaSolve(TermMatrix& A, const TermVector& B, bool useGPU=false, bool keepA=false);
TermVector lapackSolve(TermMatrix& A, const TermVector& B, bool keepA=false);
TermVector directSolve(TermMatrix&, const TermVector&, bool keepA = false);
TermVector schurSolve(TermMatrix&, const TermVector&, const Unknown&, const Unknown&, bool keepA = false);

//direct solver (few right-hand sides)
TermVectors factSolve(TermMatrix&, const vector<TermVector>&);
TermVectors ldltSolve(TermMatrix&, const vector<TermVector>&, TermMatrix&);
TermVectors ldlstarSolve(TermMatrix&, const vector<TermVector>&, TermMatrix&);
TermVectors luSolve(TermMatrix&, const vector<TermVector>&, TermMatrix&);
TermVectors gaussSolve(TermMatrix&, const vector<TermVector>&, bool keepA = false);
TermVectors umfpackSolve(TermMatrix&, const vector<TermVector>&, bool keepA = false);
TermVectors directSolve(TermMatrix&, const vector<TermVector>&, bool keepA = false);

// direct solver (TermMatrix right-hand side)
TermMatrix factSolve(TermMatrix&, TermMatrix&);
TermMatrix directSolve(TermMatrix&, TermMatrix&, KeepStatus=_keep);
TermMatrix inverse(TermMatrix&);

factorize(), factSolve() and directSolve() functions are general functions that determine automatically the adapted methods to apply.

Warning

To use umfpackSolve, magmaSolve or lapackSolve, libraries umfpack, magma, lapack-blas have to be installed and activated. directSolve() chooses umfpack solver when matrix is sparse and umfpack available, and lapack solver when matrix is dense and lapack available. umfpack solver is always faster than XLiFE++ solvers but lapack solver may be slower than the XLiFE++ gauss solver if non optimized lapack-blas libraries are used

Note that the factSolve() and directSolve() functions can use a TermMatrix as right hand side. In that case, they compute \(\mathbb{A}^{-1}\mathbb{B}\) using a factorization of \(\mathbb{A}\). The inverse() function computes the inverse of a TermMatrix using the directSolve() function with the identity matrix as right hand side. These functions provide some TermMatrix that are stored as column dense storage. So be care with memory usage!

Tip

Up to now, the usage of factSolve(), directSolve() functions with a TermMatrix as right hand side and inverse() is restricted to single unknown TermMatrix.

In a same way, interfaces to various iterative solvers are provided :

//! general iterative solver
TermVector iterativeSolveGen(IterativeSolverType isType, TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, const Real tol, const Number iterMax, const Real omega, const Number krylovDim, const Number verboseLevel);
//! general front end for iterativeSolve
TermVector iterativeSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, const vector<Parameter>& ps);

//! user front-end for iterative solver
inline TermVector iterativeSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 5 Parameter);
inline TermVector iterativeSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 6 Parameter);
inline TermVector iterativeSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 6 Parameter);
inline TermVector iterativeSolve(TermMatrix& A, TermVector& B, 0 to 6 Parameter);

//! user front-end for BiCG solver
inline TermVector bicgSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector bicgSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector bicgSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 4 Parameter);
inline TermVector bicgSolve(TermMatrix& A, TermVector& B, 0 to 4 Parameter);

//! user front-end for BiCGStab solver
inline TermVector bicgStabSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector bicgStabSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector bicgStabSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 4 Parameter);
inline TermVector bicgStabSolve(TermMatrix& A, TermVector& B, 0 to 4 Parameter);

//! user front-end for CG solver
inline TermVector cgSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector cgSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector cgSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 4 Parameter);
inline TermVector cgSolve(TermMatrix& A, TermVector& B, 0 to 4 Parameter);

//! user front-end for CGS solver
inline TermVector cgsSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector cgsSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector cgsSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 4 Parameter);
inline TermVector cgsSolve(TermMatrix& A, TermVector& B, 0 to 4 Parameter);

//! user front-end for GMRes solver
inline TermVector gmresSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector gmresSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector gmresSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 4 Parameter);
inline TermVector gmresSolve(TermMatrix& A, TermVector& B, 0 to 4 Parameter);

//! user front-end for QMR solver
inline TermVector qmrSolve(TermMatrix& A, TermVector& B, const TermVector& X0, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector qmrSolve(TermMatrix& A, TermVector& B, const PreconditionerTerm& P, 0 to 4 Parameter);
inline TermVector qmrSolve(TermMatrix& A, TermVector& B, const TermVector& X0, 0 to 4 Parameter);
inline TermVector qmrSolve(TermMatrix& A, TermVector& B, 0 to 4 Parameter);

iterativeSolve() are the front end of all other iterative methods. :cpp:func:iterativeSolveGen` are the front end of all iterative methods.

To compute eigenvalues, internal solvers or interface to arpack solvers are available:

//! general eigen solver
EigenElements eigenSolveGen(TermMatrix* pA, TermMatrix* pB, Number nev, String which, Real tol, EigenComputationalMode eigCompMode, Complex sigma, const char mode, EigenSolverType solver);
//! general eigen solver
EigenElements eigenInternGen(TermMatrix* pA, TermMatrix* pB, Number nev, String which, Real tol, EigenComputationalMode eigCompMode, Complex sigma, bool isShift);

//! general front-end for generalized eigen solver
EigenElements eigenSolve(TermMatrix& A, TermMatrix& B, vector<Parameter> ps);

//! user front-end for eigen solver
EigenElements eigenSolve(TermMatrix& A, TermMatrix& B, 0 to 10 Parameter);
EigenElements eigenSolve(TermMatrix& A, 0 to 10 Parameter);

//! user front-end for internal eigen solver
inline EigenElements eigenInternSolve(TermMatrix& A, TermMatrix& B, 0 to 9 Parameter);
inline EigenElements eigenInternSolve(TermMatrix& A, 0 to 9 Parameter);

//! user front-end for external Arpack eigen solver
inline EigenElements arpackSolve(TermMatrix& A, TermMatrix& B, 0 to 9 Parameter);
inline EigenElements arpackSolve(TermMatrix& A, 0 to 9 Parameter);

The EigenElements class handles the list of eigenvalues and the list of eigenvectors. See the TermVector section.

Warning

arpack solver are available only if arpack library is installed.

When addressing integral representations, say \(r(x)=\int_{\Sigma}op(K)(x,y)*op(u)(y)\,dy\) one can be interested in the matrix with coefficients \(r_{ij}=\int_{\Sigma}op(K)(x_i,y)*op(w_j)(y)\,dy\) where \((x_i)_i\) are some points and \((w_j)_j\) some shape functions related to the unknown \(u\). Special functions, named integralFunction() will produce such matrices embedded in a TermMatrix object:

TermMatrix integralRepresentation(const Unknown&, const GeomDomain&, const LinearForm&);
TermMatrix integralRepresentation(const GeomDomain&, const LinearForm&);
TermMatrix integralRepresentation(const vector<Point>&, const LinearForm&);

When no domain is explicitly passed, one shadow PointsDomain object will be created from the list of points given. When no unknown is explicitly passed, one (minimal) space and related shadow unknown will be created to represent the row unknown. These functions call the fundamental computation function:

template<typename T, typename K>
void SuTermMatrix::computeIR(const SuLinearForm&f, T*, K&, const vector<Point>& xs);

Once a TermMatrix is computed, it is possible to access to one of its coefficient and to change its value. Because, TermMatrix is a block matrix indexed by unknowns, a pair of unknowns has to be specified except if it is a single unknown matrix. Row index and col index of the sub-matrix coefficient may be specified either by numbers or by dofs:

Value getValue(Number, Number) const;
Value getValue(const Unknown&, const Unknown&, Number, Number) const;
void  setValue(Number, Number, const Value&);
void  setValue(const Unknown&, const Unknown&, Number, Number, const Value&);
Value getValue(const Dof& du, const Dof& dv) const;
void  setValue(const Dof& du,const Dof& dv,const Value& val);
Value getValue(const Unknown& u,const Unknown& v,const Dof& du,const Dof& dv) const;
void  setValue(const Unknown& u,const Unknown& v, const Dof& du, const Dof& dv, const Value& val);

These functions use some Value objects that have to be real/complex scalars or real/complex matrices according to the matrix coefficient type!

There exists also functions that addresses scalar representation when matrix is related to vector unknown:

Value getScalarValue(const Unknown&, const Unknown&, Number, Number, Dimen=0, Dimen=0) const;
void setScalarValue(const Unknown&, const Unknown&, Number, Number, const Value&, Dimen=0, Dimen=0);
Value getScalarValue(Number, Number, Dimen=0, Dimen=0) const;
void setScalarValue(Number, Number, const Value&, Dimen=0, Dimen=0);

The following function can assign a same value to rows or columns:

void  setRow(const Value&, Number r1,Number r2);
void  setCol(const Value&, Number c1,Number c2);
void  setRow(const Unknown&, const Unknown&, const Value&, Number r1, Number r2);
void  setCol(const Unknown&, const Unknown&, const Value&, Number c1, Number c2);
void  setRow(const Value& val, const Dof& d);
void  setCol(const Value& val, const Dof& d);
void  setRow(const Unknown& u, const Unknown& v, const Value& val, const Dof& d);
void  setCol(const Unknown& u, const Unknown& v, const Value& val, const Dof& d);

The link between dof and row/col index is given by the following functions:

Number rowRank(const Dof&) const;
Number colRank(const Dof&) const;
Number rowRank(const Unknown&, const Unknown&, const Dof&) const;
Number colRank(const Unknown&, const Unknown&, const Dof&) const;

Tip

The setValue(), setRow(), setCol() functions never modify the matrix storage!

Warning

These functions are no longer available if the matrix has moved to its global representation and lost its block representation!

Finally some print and export functions are provided:

//as member function
void print(ostream&) const;
void viewStorage(ostream&) const;
void saveToFile(const String&, StorageType, bool=false) const;
//as non member function
void saveToFile(const String&, const TermMatrix&, StorageType, bool enc = false);

See also

TermMatrix infos:

• library=term

• header=TermMatrix.hpp,

• implementation=TermMatrix.cpp,

• test=test_TermMatrix.cpp,

• header dep=SuTermMatrix.hpp, termUtils.hpp, Term.hpp, form.h, config.h, utils.h

The SuTermMatrix class

The SuTermMatrix class carries numerical representation of a single unknown pair bilinear form and more generally any matrix attached to a pair of unknowns (row unknown and row column).

Hint

By convention, ‘u’ refers to column (unknown of bilinear form) and ‘v’ to row (test function in bilinear form).

class SuTermMatrix : public Term
{
 protected :
  SuBilinearForm* sublf_p;            //bilinear form through pointer
  const Unknown* u_p;                 //column unknown
  const TestFunction* v_p;            //row unknown
  mutable Space* space_u_p;           //pointer to u-space
  mutable Space* space_v_p;           //pointer to v-space
  vector<Space *> subspaces_u;   //u-subspaces involved
  vector<Space *> subspaces_v;   //v-subspaces involved
  MatrixEntry* entries_p;             //matrix as LargeMatrix
  MatrixEntry* scalar_entries_p;      //scalar matrix as LargeMatrix
  vector<DofComponent> cDoFs_u;  //component u-DoF list
  vector<DofComponent> cDoFs_v;  //component v-DoF list
  MatrixEntry* rhs_matrix_p;          //correction matrix when essential cond.
}

The sublf_p contains a pointer to a SuBiLinearForm (single unknown pair bilinear form). It may be null, that means there is no explicit bilinear form attached to the SuTermMatrix.

The space_u_p (resp. space_u_p) pointer points to the largest subspace involved in SuTermMatrix columns (resp. rows). These pointers should never be null because they carry the row and column DoFs numbering.

For this reason too, the largest subspaces have to be correctly updated during any operation on SuTermMatrix. The Space* vector subspaces_u (resp. subspaces_v ) contains the subspaces (as subspace of the largest space) attached to basic bilinear forms defined in the SuBiLinearForm pointer (if defined), see buildSubspaces() function.

Warning

Do not confuse the space_u_p pointer and u_p->space_p pointer that specifies the whole space. They may be the same!

The numerical representation of matrix is defined in the entries_p MatrixEntry pointer as a real/complex matrix or a real/complex matrix of matrices, regarding the value type (real or complex) and the structure of the unknowns (scalar or vector).

If required, matrix of matrices representation may be expanded to a matrix of scalars stored in the scalar_entries_p MatrixEntry pointer. In that case, the cDoFs_u and cDoFs_v vectors of DofComponent give the row and column numbering (in DofComponent) of entries. Note that if SuTermMatrix is of scalar type, scalar_entries_p = entries_p.

In case of essential conditions applied to, rhs_matrix_p MatrixEntry pointer may be allocated to store the eliminated part of SuTermMatrix. Note that, SuTermMatrix class does not manage SetOfConstraints objects, the treatment of essential condition being driven by TermMatrix!

The SuTermMatrix class also handles HMatrix (hierarchical matrix):

HMatrixEntry<FeDof>* hm_entries_p; //hierarchical matrix
HMatrixEntry<FeDof>* hm_scalar_entries_p; //scalar hierarchical matrix
ClusterTree<FeDof>*  cluster_u;    //column cluster tree
ClusterTree<FeDof>*  cluster_v;    //row cluster tree

HMatrix stuff is described in chapter H-matrices. Let’s remember that the hierarchical matrix are built from the clustering of row and column indices (cluster_u, cluster_v). There are two HMatrixEntry pointers, one to handle any matrix (scalar or matrix), the other one to handle the scalar representation of a matrix of matrices if it is required. When HMatrix is a scalar one, both the pointers are the same.

The SuTermMatrix class provides some constructors from bilinear form, a constructor from SuTermVector (diagonal matrix), a constructor from row dense matrix, a constructor from linear combination and a copy constructor:

// basic constructor
SuTermMatrix(const Unknown*, Space*, const Unknown*, Space*, MatrixEntry*, const String& na="");
//constructor from bilinear form
SuTermMatrix(SuBilinearForm* sublf = 0, const String& na="", bool noass=false);
SuTermMatrix(SuBilinearForm* sublf = 0, const String& na="", ComputingInfo cp= ComputingInfo());
SuTermMatrix(SuBilinearForm*, const Unknown*, const Unknown*, Space*, Space*, const vector<Space *>&, const vector<Space *>&, const String&, MatrixEntry* =0);
//constructor of diagonal matrix
SuTermMatrix(SuTermVector &, const String& na="");
SuTermMatrix(const Unknown*, Space*, const Unknown*, Space*, SuTermVector&, StorageType=_noStorage, AccessType=_noAccess, const String& na="");
void diagFromSuTermVector(const Unknown*, Space*, const Unknown*,Space*, SuTermVector&, StorageType=_noStorage, AccessType=_noAccess, const String& na="");
// constructor from a row dense matrix
SuTermMatrix(const Unknown*, Space*, const Unknown*, Space*, const vector<T>&, number_t, number_t, const string_t& ="");
//constructor from linear combination
SuTermMatrix(const LcTerm&,const String& na="");
//copy constructor and assign operator
SuTermMatrix(const SuTermMatrix&,const String& na="");
void copy(const SuTermMatrix&);
SuTermMatrix& operator=(const SuTermMatrix&);
//destructor, clear
virtual ~SuTermMatrix();
void clear();

There is no specific constructor for SuTermMatrix of type Hmatrix. It is induced by some properties of the bilinear form; more precisely by a particular choice of integration method.

It provides a lot of accessors and property functions:

TermType termType() const;
ValueType valueType() const;
StrucType strucType() const;
Space& space_u() const;
Space& space_v() const;
Space* space_up() const;
Space* space_vp() const;
Space*& space_up();
Space*& space_vp();
const Unknown* up() const;
const Unknown* vp() const;
const Unknown*& up();
const Unknown*& vp();
MatrixEntry*& entries();
const MatrixEntry* entries() cons;
MatrixEntry*& scalar_entries();
const MatrixEntry* scalar_entries() const;
MatrixEntry*& rhs_matrix();
const MatrixEntry* rhs_matrix() const;
const vector<DofComponent>& cDoFsu() const;
const vector<DofComponent>& cDoFsv() cons;
vector<DofComponent>& cDoFsu();
vector<DofComponent>& cDoFsv();
SymType symmetry() const;
StorageType storageType() const;
MatrixStorage* storagep() const;
void setStorage(StorageType, AccessType);
void toStorage(StorageType, AccessType);

The main computation functions and related stuff follow:

void compute();
void compute(const LcTerm&,const String& na="");
template<unsigned int CM>
  void compute(const vector<SuBilinearForm>&, ValueType, StrucType);
template<typename T, typename K>
  void computeIR(const SuLinearForm&f, T*, K&, const vector<Point>&);

void buildSubspaces();
void setStorage(StorageType, AccessType);
void toStorage(StorageType, AccessType);
void addDenseToStorage(const vector<SuBilinearForm>&,MatrixStorage*) const;
void toScalar(bool keepEntries=false);
vector<SuBilinearForm> getSublfs(ComputationType, ValueType&) const;
void updateStorageType(const vector<SuBilinearForm>&,set<Number>&, set<Number>&,StorageType&) const;

SuTermMatrix may be modified by the following algebraic operators:

template<typename T>
SuTermMatrix& operator*=(const T&);
template<typename T>
  SuTermMatrix& operator/=(const T&);
SuTermMatrix& operator+=(const SuTermMatrix&);
SuTermMatrix& operator-=(const SuTermMatrix&);
friend SuTermVector operator*(const SuTermMatrix&, const SuTermVector&);
friend SuTermMatrix operator*(const SuTermMatrix&, const SuTermMatrix&);

It is also possible to access to one matrix coefficient, to change it, to assign a given value to a row or a column:

Value getValue(number_t, number_t) const;
Value getScalarValue(number_t, number_t, dimen_t=0, dimen_t=0) const;
void  setValue(number_t, number_t, const Value&);
void  setScalarValue(number_t, number_t, const Value&, dimen_t=0, dimen_t=0);
void  setRow(const Value&, number_t r1, number_t r2);
void  setCol(const Value&, number_t r1, number_t r2);
number_t rowRank(const Dof&) const;
number_t rowRank(const DofComponent&) const;
number_t colRank(const Dof&) const;
number_t colRank(const DofComponent&) const;

The row/col index may be either numbers or DoFs; the link between DoF and index number is got using rowRank(), colRank() functions.

Hint

The setValue, setRow, setCol functions never modify the matrix storage!

Finally, there are some print and export stuff:

void print(ostream&) const;
void print(ostream&, bool) const;
void viewStorage(ostream&) const;
void saveToFile(const String&, StorageType, bool=false) const;

Most of the previous functions works when SuTermMatrix handles a HMatrix, but some not. As there is no check, be cautious! Besides, there are some specific functions related to Hmatrix representation:

bool hasHierarchicalMatrix() const;
HMatrix<T,FeDof>& getHMatrix(StrucType str=_undefStrucType) const;

See also

• library=term,

• header=SuTermMatrix.hpp,

• implementation=SuTermMatrix.cpp,

• test=test_TermMatrix.cpp,

• header dep= Term.hpp, LcTerm.hpp, termUtils.hpp, form.h, config.h, utils.h

The LcTerm class

The LcTerm class is a template class handling a linear combination of terms of type TermVector, TermMatrix, SuTermVector or SuTermMatrix. It is automatically involved as a result whenever any linear combination of Term’s is handled:

TermVector tv1, tv2;
\...
out<<norm2(tv1-tv2);

In this example, tv1-tv2 produces a LcTerm<TermVector> that is cast implicitly to a TermVector because the definition of a constructor of TermVector from a LcTerm<TermVector>. Then any functions defined on TermVector may be applied, the norm2 function in this example.

The LcTerm class inherits from vector<pair<const TT *, complex_t >>

template <typename TT>
class LcTerm : public vector<pair<const TT *, complex_t> >
{
 public:
  string_t nametype;
  typedef typename vector<pair<const TT *, complex_t> >::iterator iterator;
  typedef typename vector<pair<const TT *, complex_t> >::const_iterator const_iterator;

It has template constructors and insertion functions (push_back()):

template<typename T>
  LcTerm(const TT*,const T&);
  LcTerm(const TT*,const T&, const TT*, const T&);
  LcTerm(const TT&,const T&);
  LcTerm(const TT&,const T&, const TT&, const T&);
  LcTerm(const vector<const TT *>&, const vector<T>&);
  void push_back(const Term*,const T&);
  void push_back(const Term&,const T&);

and to avoid some std::vector member functions are overloaded:

number_t size() const ;
const_iterator begin();
const_iterator end();
iterator begin();
iterator end();

It supports the following algebraic operations:

template<typename T>
  LcTerm<TT>& operator*=(const T&);
  LcTerm<TT>& operator/=(const T&);
  LcTerm<TT>& operator+=(const LcTerm<TT>&);
  LcTerm<TT>& operator-=(const LcTerm<TT>&);

and provides the following utilities

ValueType coefType() const;
void print(ostream &) const;
template <typename TX>
friend ostream& operator<<(ostream &,const LcTerm<TX>&)

Note that TermVector and TermMatrix classes have functions that create some LcTerm objects.

See also

• library=term,

• header=LcTerm.hpp,

• implementation=LcTerm.cpp,

• test=,

• header dep= Term.hpp, termUtils.hpp, form.h, config.h, utils.h

The SymbolicTermMatrix class

Sometimes, numerical methods involve more complex combinations of TermMatrix than linear combinations, for instance \(\mathbb{A}=\mathbb{M} + \mathbb{K} \mathbb{M}^{-1}\mathbb{K}^t\) where \(\mathbb{M}\) and \(\mathbb{K}\) are sparse matrices. Generally, it is not a good idea to compute \(\mathbb{A}\) because the result is a dense matrix. The purpose of the SymbolicTermMatrix class is to describe as symbolic this matrix, not to compute it but to compute \(\mathbb{A}X\) with \(X\) a TermVector. A SymbolicTermMatrix object is a node of the binary tree with the following data :

• A symbolic operation (one of id, +, -,*, /, inv, tran, conj, adj);

• A TermMatrix object (pointer to), may be 0;

• Up to two SymbolicTermMatrix objects (pointer to);

• A coefficient (complex scalar) applied to the operation.

Using these data, the symbolic form of the \(\mathbb{A}\) matrix is presented on figure Symbolic TermMatrix. On a node, there is either a TermMatrix (leaves) or a pair of SymbolicTermMatrix.

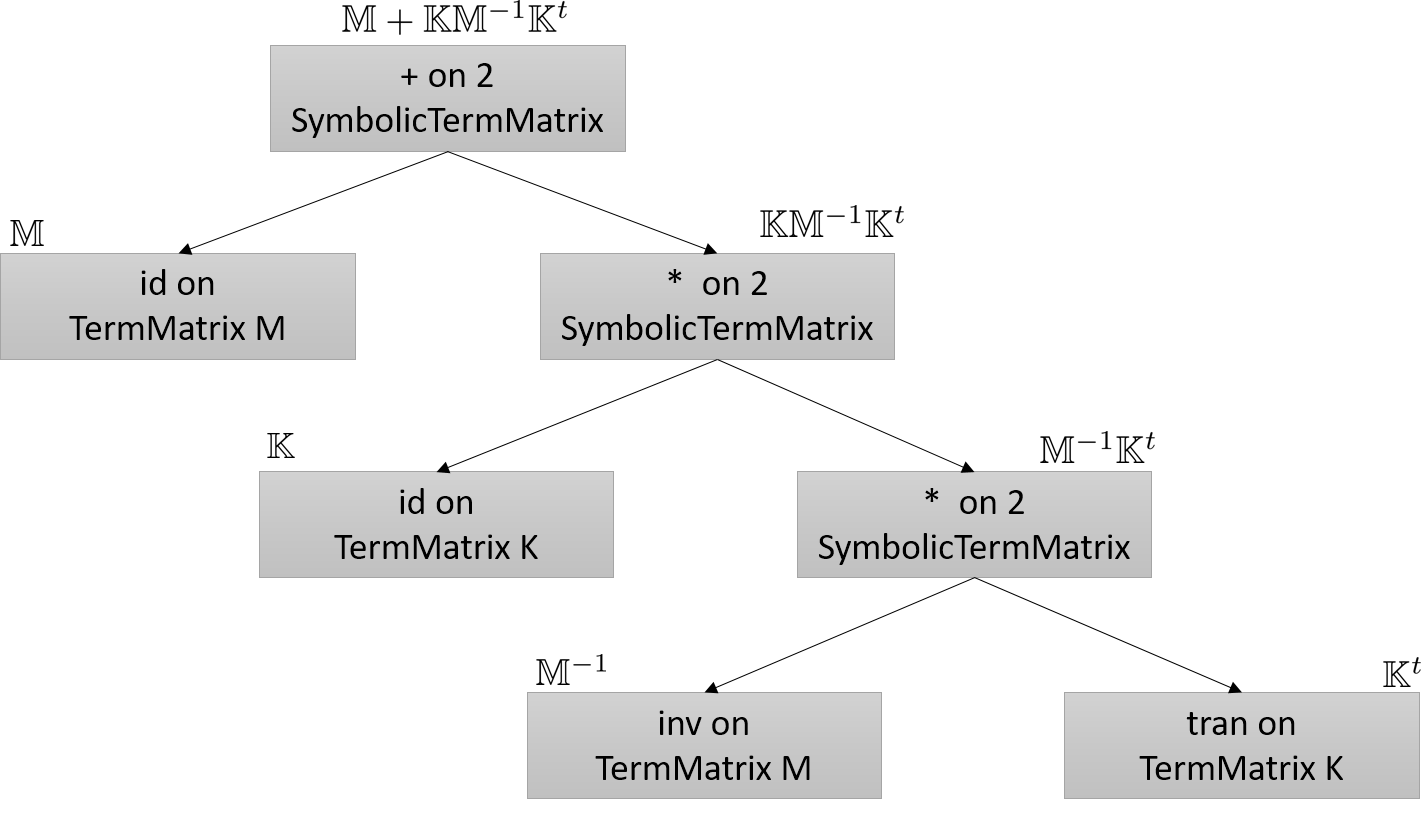
Fig. 149 Symbolic TermMatrix

So the SymbolicTermMatrix class has the following data members

class SymbolicTermMatrix
{
  public:
   SymbolicTermMatrix* st1_, *st2_;
   const TermMatrix* tm_;
   Complex coef_;
   SymbolicOperation op_;
   bool delMat_;
  ...
}

the following constructors and destructor stuff

SymbolicTermMatrix();
SymbolicTermMatrix(const TermMatrix&, const complex_t& =complex_t(1.,0.));
SymbolicTermMatrix(SymbolicOperation, SymbolicTermMatrix*, SymbolicTermMatrix*=0);
SymbolicTermMatrix(LcTerm<TermMatrix>& lc);
~SymbolicTermMatrix();
void add(LcTerm<TermMatrix>&, std::vector<std::pair<const TermMatrix*, complex_t> >::iterator);
SymbolicTermMatrix(const SymbolicTermMatrix&);
SymbolicTermMatrix& operator=(const SymbolicTermMatrix&);

The delMat variable is a flag telling the TermMatrix can be deleted because one of the constructors creates a copy of the original one.

SymbolicTermMatrix();
SymbolicTermMatrix(const TermMatrix&, const complex_t& =complex_t(1.,0.));
SymbolicTermMatrix(SymbolicOperation, SymbolicTermMatrix*, SymbolicTermMatrix*=0);
SymbolicTermMatrix(LcTerm<TermMatrix>& lc);
~SymbolicTermMatrix();
void add(LcTerm<TermMatrix>&, std::vector<std::pair<const TermMatrix*, complex_t> >::iterator);
SymbolicTermMatrix(const SymbolicTermMatrix&);
SymbolicTermMatrix& operator=(const SymbolicTermMatrix&);

The class offers classic print stuff :

string_t asString() const;
void print(std::ostream&) const;
void print(PrintStream& os) const {print(os.currentStream());}
friend std::ostream& operator<<(std::ostream& ,const SymbolicTermMatrix&)

Besides, a lot of operators are provided:

SymbolicTermMatrix& operator *(const TermMatrix&,SymbolicTermMatrix&);
SymbolicTermMatrix& operator *(SymbolicTermMatrix&, const TermMatrix&);
SymbolicTermMatrix& operator +(const TermMatrix&,SymbolicTermMatrix&);
SymbolicTermMatrix& operator +(SymbolicTermMatrix&, const TermMatrix&);
SymbolicTermMatrix& operator -(const TermMatrix&,SymbolicTermMatrix&);
SymbolicTermMatrix& operator -(SymbolicTermMatrix&, const TermMatrix&);
SymbolicTermMatrix& operator +(LcTerm<TermMatrix>&,SymbolicTermMatrix&);
SymbolicTermMatrix& operator +(SymbolicTermMatrix&, LcTerm<TermMatrix>&);
SymbolicTermMatrix& operator -(LcTerm<TermMatrix>&,SymbolicTermMatrix&);
SymbolicTermMatrix& operator -(SymbolicTermMatrix&, LcTerm<TermMatrix>&);
SymbolicTermMatrix& operator *(LcTerm<TermMatrix>&,SymbolicTermMatrix&);
SymbolicTermMatrix& operator *(SymbolicTermMatrix&, LcTerm<TermMatrix>&);
SymbolicTermMatrix& operator *(SymbolicTermMatrix&, SymbolicTermMatrix&);
SymbolicTermMatrix& operator +(SymbolicTermMatrix&, SymbolicTermMatrix&);
SymbolicTermMatrix& operator -(SymbolicTermMatrix&, SymbolicTermMatrix&);
SymbolicTermMatrix& conj(SymbolicTermMatrix&);
SymbolicTermMatrix& adj(SymbolicTermMatrix&);
SymbolicTermMatrix& tran(SymbolicTermMatrix&);
SymbolicTermMatrix& operator *(SymbolicTermMatrix&, const complex_t&);
SymbolicTermMatrix& operator *(const complex_t&, SymbolicTermMatrix&);
SymbolicTermMatrix& operator /(SymbolicTermMatrix&, const complex_t&);
SymbolicTermMatrix& inv(const TermMatrix&);
SymbolicTermMatrix& inv(SymbolicTermMatrix&);

Because some syntaxes may be ambiguous, the operator ~ is overloaded in order to move a TermMatrix to a SymbolicTermMatrix:

SymbolicTermMatrix& operator~(const TermMatrix&):

The most important functions are function that compute recursively the matrix vector product \(\mathbb{A}X\) :

TermVector operator*(const SymbolicTermMatrix&, const TermVector&);
TermVector multMatrixVector(const SymbolicTermMatrix&, const TermVector&);
TermVector operator*(const TermVector&, const SymbolicTermMatrix&);
TermVector multVectorMatrix(const TermVector&, const SymbolicTermMatrix&);

See also

• library=term,

• header=SymbolicTermMatrix.hpp,

• implementation=SymbolicTermMatrix.cpp,

• test=unit_TermMatrix.cpp,

• header dep= TermMatrix.hpp, config.h, utils.h

The computation algorithms

Matrix computation

In this section, we explain how the computation of matrix from bilinear form works.

This computation depends on the type of the bilinear form (single integral term, double integral term, ….) and the types of unknown and test function. This section addresses only the computation of SuTermMatrix.

The principle of computation, implemented in SuTermMatrix::compute(), consists in 4 steps:

• collect basic bilinear forms along their domain and their computation type (see SuTermMatrix::getSuBlfs() function.):

  _FEComputation	single integral on a domain	u, v in FE spaces
  _FEextComputation	single integral on a boundary domain with non-tangential derivatives	u, v in FE spaces
  _DGComputation	single integral on a side domain involving mean-jump operators	u, v in FE spaces (discontinuous)
  _IEComputation	double integral on a domains pair	u, v in FE spaces, standard Kernel
  _SPComputation*	single integral on a domain	u, v in FE spaces
  _FESPComputation	single integral on a domain	u, v in FE spaces, other in FE space
  _IESPComputation	single integral on a domain pair	u, v in FE spaces, TensorKernel
  _IEHMComputation	single integral on a domain pair	u, v in FE spaces, HMatrix

• construct a storage consistent with all collections to compute (imposed by user or chosen between compressed sparse storage or dense storage)

• create MatrixEntry with the right structure and value types

• for each collection, call the computation function regarding its computation type

This last step looks like in SuTermMatrix::compute():

if(FEsublfs.size()>0)    compute<_FEComputation>(FEsublfs, vt, str);
if(FEextsublfs.size()>0) compute<_FEextComputation>(FEextsublfs, vt, str);
if(SPsublfs.size()>0)    compute<_SPComputation>(SPsublfs, vt, str);
if(FESPsublfs.size()>0)  compute<_FESPComputation>(FESPsublfs, vt, str);
if(IEsublfs.size()>0)    compute<_IEComputation>(IEsublfs, vt, str);
if(IEextsublfs.size()>0) compute<_IEComputation>(IEextsublfs, vt, str);
if(IESPsublfs.size()>0)  compute<_IESPComputation>(IESPsublfs, vt, str);
if(DGsublfs.size()>0)    compute<_DGComputation>(DGsublfs, vt, str);

where all specializations of compute are implemented in the XXMatrixComputation.hpp files included add the end of the SuTermMatrix.hpp file. All the computation algorithms mainly work as follows:

retry general data (spaces, subspaces, domains, ...)
loop on element on domain 1
retry element data (local to global numbering)
(loop on element on domain 2)     only for IE and IESP computation
  (retry element data)
   compute shapevalues
   loop on basic bilinear form
      loop on quadrature points
         compute operator on unknowns
        add in elementary matrix using tensorial operations
      assembly in global matrix

Hint

For sake of simplicity, evaluation of operators returns always a textbf{scalar vector}, even if the unknowns are vector ones. So this vector has to be correctly reinterpreted when it is added in elementary block matrix.

When there is a HMatrix computation that requires a specific representation (HMatrixEntry), this one is achieved after all the computations requiring a HMatrixEntry. Then the MatrixEntry (if it exists one) is merged in the HMatrixEntry. Obviously, anything cannot be merged to HMatrixEntry!

For IE computation, some specialized function are devoted to particular integration method adapted to singular kernels (Sauter-Schwab method for instance). They are implemented in particular files (SauterSchwabIM.hpp, LenoirSallesIM.hpp, DuffyIM.hpp), see the src/term/computation directory.

Up to now, most of the computation functions have been parallelized (multi-threading with omp).

Understanding TermMatrix operations

The following figure sketches out how the operations are processed in the class hierarchy from TermMatrix to storage classes that implement the computation algorithms:

Fig. 150 The process of a TermMatrix operation

Vector computation

For the moment, the SuTermVector class provides

• the computeFE() function that computes single integral on a FE space

• the :cpp:func`computeIR`` function that computes integral representation

These functions are implemented in the textit{FeVectorComputation.hpp} file included by the textit{SuTermVector.hpp} file. It works as matrix computation but it is simpler.

The Projector class

The Projector class is intended to handle projection from one FE space, say \(V\) to another FE space, say \(W\). The projection \(w\in W\) of a \(v \in V\) is based on a bilinear form, say \(a(.,.)\), defined on both spaces :

\[a(w,\tilde{w}) =a(v,\tilde{w})\, \ \forall \tilde{w}\in W.\]

Let \((w_i)_{i=1,n}\) a basis of \(W\) and \((v_i)_{i=1,m}\) a basis of \(V\), the above problem is equivalent to the matrix problem:

\[\mathbb{A}\,W=\mathbb{B}\,V\]

where \(\mathbb{A}_{ij}=a(w_j,w_i)\), \(\mathbb{B}_{ij}=a(v_j,w_i)\), \(v=\sum_{i=1,m}V_i\,v_i\) and \(w=\sum_{i=1,n}W_i\,w_i\).

The bilinear form should be symmetric and positive on the space \(W\) in order to the matrix \(\mathbb{A}\) be invertible. The most simple example is the \(L^2\) projection related to the bilinear form:

\[a(w,\tilde{w})=\int_{\Omega }w\,\tilde{w}\,d\Omega.\]

As a consequence, the Projector class manages the following data:

class Projector
{
 public:
  ProjectorType projectorType;  //!< type of projection
  string_t name;                //!< name of projection
  protected:
  Space* V_, *W_;               //!< spaces involved
  Unknown* u_V, *u_W;           //!< internal unknowns
  const GeomDomain* domain_;    //!< domain  involved in bilinear forms
  BilinearForm* a_V, *a_W;      //!< bilinear forms used by projector
  mutable TermMatrix* A_, *B_;  //!< matrix a(W,W) and a(W,V)
  mutable TermMatrix* invA_B;   //!< matrix inv(A)*B if allocated
}

where the projector type is one of the following:

Because, bilinear forms in XLiFE++ are linked to unknowns/spaces, the class manages two bilinear forms and their matrix representation. The unknowns used by the Projector are not some user unknowns but are specific to the class. Finally, it can allocate a TermMatrix object representing the matrix \(\mathbb{A}^{-1}\,\mathbb{B}\).

Besides, in order to save time and memory, all the projectors that have been handled (explicitly or implicitly) are listed in a static vector:

static std::vector<Projector*> theProjectors;

Projector are constructed from spaces, a projector type or a bilinear form and an optional name. When dealing with the restriction of a space to a domain, the domain has to be given. When dealing with projection of vector unknown, the sizes have to be specified.

Projector(Space& V, Space& W, ProjectorType pt=_L2Projector, const string_t& na="");
Projector(Space& V, Space& W, const GeomDomain&, ProjectorType pt=_L2Projector, const string_t& na="");
Projector(Space& V, Space& W, BilinearForm& a, const string_t& na="");
Projector(Space& V, dimen_t nbcV, Space& W, dimen_t nbcW, ProjectorType pt=_L2Projector, const string_t& na="");
Projector(Space& V, dimen_t nbcV, Space& W, dimen_t nbcW, const GeomDomain&, ProjectorType pt=_L2Projector, const string_t& na="");
Projector(Space& V, dimen_t nbcV, Space& W, dimen_t nbcW, BilinearForm& a, const string_t& na="");
~Projector();
void init(dimen_t nbc_V, dimen_t nbc_W);

The init function does really the job of construction. In particular, it computes the matrix A_ and B_ and do a factorization of A_.

Note that the TermMatrix is not allocated at the construction. To allocate it, one has to call the member function:

TermMatrix& asTermMatrix(const Unknown&, const Unknown&, const string_t& = "invA_B");

that returns a reference to the TermMatrix invA_B and deletes the TermMatrix A_ and B_.

Once constructed, projectors can process TermVector’s by using one of the three operator functions:

TermVector operator()(TermVector& V,const Unknown& u) const;
TermVector operator()(const TermVector& V) const;
TermVector& operator()(TermVector& V, TermVector& PV) const;

Because an unknown is always linked to any TermVector, the user can pass the unknown either in an explicit way or in an implicit way when the TermVector result is passed to the operator. When no unknown is passed to, the unknown of the projection will be the first unknown linked to the space \(W\). If the TermMatrix invA_B is allocated, the projection does the product invA_B * V, if not the projection does the product B_ * V and solve the linear system A_ * X = B_ * V using the factSolve functions.

Projection can also be processed by using the operator *:

friend TermVector operator*(const Projector& P, const TermVector& V);

that only calls P(V).

Users can compute the projection of a TermVector without instantiating a Projector object:

TermVector projection(const TermVector& V, Space& W, ProjectorType pt=_L2Projector);

In that case, a Projector object is created in the back.

Two functions deal with the list of all projectors:

friend Projector& findProjector(Space& V, Space& W, ProjectorType pt=_L2Projector);
static void clearGlobalVector();

The findProjector creates a new projector if projector has not been found.

Finally, there are some print stuff:

void print(ostream&) const;
friend ostream& operator<<(ostream&, const Projector&);

See also

• library=term,

• header=Projector.hpp,

• implementation=Projector.cpp,

• test=unit_Projector.cpp,

• header dep= Term.hpp, config.h, utils.h