Post-processing#

Save data to external files#

We want to exploit easily the data contained in the objects produced during the computation. The objects concerned are mainly TermVector objects since TermVector is the type of nearly all the computation results of interest to the user. This may also concern TermMatrix objects if further postprocessing is envisaged.

As mentionned just above, printing objects using the << operator may produce big files containing a lot of information, generally used to control the different steps of the computation. But we often need to handle the data values outside XLiFE++, either in a raw format or in a specific one corresponding to some particular software.

The saveToFile external routines have been designed for that purpose.

They all work with the same pattern. First argument is the file name, with or without its extension. The second argument is the object yyou want to save. It can be a Mesh, a TermMatrix, a TermVector, a TermVectors, a EigenElements or a SvdElements. Then come the optional arguments with a key-value system.

The key _format, available for all the above-mentioned objects but TermMatrix, concerns the file format. Thhe most important thing to know about this key is that if the filename contains an authorized extension, this extension will always be prior to the value given to _format. Authorized extensions depend on the object to be saved.

Save a Mesh#

Authorized file extensions are:

  • .msh for Gmsh format (msh)

  • .vtk for Paraview VTK format (vtk)

  • .mel for Melina format (mel)

Mesh m(...);
saveToFile("mesh.msh", m); // will produce a file mesh.msh with the gmsh format
saveToFile("mesh", m, _format=vtk); // will produce a file mesh.vtk with the vtk format

You have an additionnal parameter to control if your Mesh save generates only one file (key _aFilePerDomain without value, the default behavior), or a file per domain (key _aFilePerDomain without value).

Save a TermVector, a TermVectors, a EigenElements or a SvdElements#

For these objects, authorized file extensions are:

  • .msh for Gmsh format (msh)

  • .vtk for Paraview VTK format (vtk)

  • .vtu for Paraview VTU format (vtu)

  • .m for Matlab script format (matlab)

  • .xyzv for xyzv format (Data are stored in four columns : \(x_i \quad y_i \quad z_i \quad \mathrm{val}_i\))

  • .txt for raw format

Mesh m(Rectangle(_origin=Point(0.,0.), _xlength=5, _ylength=2, _hsteps=0.01, _domain_name="Omega"), _generator=structured);
...
Space V(_domain=omega, ...);
...
TermVector U(...);
saveToFile("U.msh", U); // will produce a file U_Omega.msh with the gmsh format
saveToFile("U", U, _format=vtu); // will produce a file U_Omega.vtu with the vtu format

Hint

For a TermVector, between the file name and optional parameters, you can give up to 4 TermVector objects.

For TermVectors, files names will be numbered, one for each TermVector.

For EigenElements and SvdElements, eigen/svd vectors will be managed as a TermVectors. There will be an additional file with the suffix eigenvalues/singularvalues and extension .txt.

Example:

EigenElements ees=eigenSolve(...);
saveToFile("EES.vtu", ees); // generates EES_eigenvalues.txt and EES_1_Omega.vtu, EES_2_Omega.vtu, ...

As for Mesh, you have an additionnal parameter to control if your save generates only one file (key _aFilePerDomain without value), or a file per domain (key _aFilePerDomain). Thhe difference hhere is that the default value is a file per domain.

At last, instead of renaming a TermVector (or TermVectors, …), you can use the key _data_name in saveToFile

Save a TermMatrix#

For a TermMatrix, keys are different. Here, you have the key _storage to set the storage in which the matrix will be saved : coo for coordinate format (the Matlab sparse format) or dense format. Dedicated extension is respectively .coo and .txt.

You also have the ability to encode file names by adding a suffix built from unknown, test function (key _encodingFilename) or not (key _noEncodingFilename, the default).

Integral representation#

In the context of integral equation, the solution of IE is a potential on the boundary ( \(\Gamma\) ). This potential is not easy to interpret, so the final step of a BEM is often the reconstruction of the field outside \(\Gamma\). For instance, the Helmholtz diffraction Dirichlet problem may be solved using a single layer potential \(q = \left[ \partial_n u \right]_{\Gamma}\) and the diffracted field outside the boundary \(\Gamma\) is given by

\[u(x) = \int_{\Gamma} G(x,y) q(y) dy.\]

XLiFE++ adresses the general form of integral representation:

\[\DeclareMathOperator{\opk}{opk} \DeclareMathOperator{\opu}{opu} u(x) = \int_{ \Gamma } \opk\left( G(x,y)\right) \otimes \opu \left(q(y) \right)\; dy.\]

where \(\DeclareMathOperator{\opk}{opk}\opk\) is an operator on kernel, \(\DeclareMathOperator{\opu}{opu}\opu\) an operator on unknown and \(\otimes\) one of the operation \(∗\), \(|\), \(^{\land}\) or \(\%\). The previous example corresponds to \(opk=id,\; \; opu=id\) and \(\otimes = *\). To deal with such integral representation, the user has to define a linear form from intg() constructor:

LinearForm ri=intg(Gamma, G*q); //default integration method
LinearForm ri=intg(Gamma, G*q, _quad=GaussLegendre, _order=3);//specifying quadrature rule
IntegrationMethods ims(_quad=GaussLegendre, _order=10, _bound=1., _quad=GaussLegendre, _order=3);
LinearForm ri=intg(Gamma, G*q, _method=ims); //specifying 2 quadrature rules

In these expressions, \(\Gamma\) is a Domain object, G a Kernel object and q an Unknown object. Singular integration method is required if you intend to evaluate the integral representation at points close to the boundary \(\Gamma\).

The linear form may be a linear combination of intg:

IntegrationMethods ims(_quad=GaussLegendre, _order=10, _bound=1., _quad=GaussLegendre, _order=3);
LinearForm ri=intg(Gamma, G*q, _method=ims) + intg(Gamma, (grad_x(G)|_nx)*q, _method=ims)

There are several methods to compute the integral representation.

Direct method#

To effectively compute integral representation you have to specify the vector representing the numerical potential, a TermVector object (say Q) and the points where to evaluate it. There are many way to give points:

  • compute at one point x:

    LinearForm ri=intg(Gamma, G*q, _quad=GaussLegendre, _order=3);
Vector<Point> xs(10);
xs(1)= Point(0,0,2); ...
Vector<Complex> val(10);
integralRepresentation(xs, ri, Q, val);

  • compute at an implicit list of points of a Domain object (say omega):

    LinearForm ri=intg(Gamma, G*q, _quad=GaussLegendre, _order=3);
Vector<Point> xs;
Vector<Complex> val;
integralRepresentation(omega, ri, Q, val, xs); // val and xs are filled by function

  • compute at an implicit list of node points of an interpolation on a Domain :

    LinearForm ri=intg(Gamma, G*q, _quad=GaussLegendre, _order=3);
TermVector U=integralRepresentation(u, omega, ri, Q); //u unknown on a Lagrange Space

Hint

In the previous syntaxes, the type of output val has to be consistent with data. For instance, val is of complex type if G or Q is of complex type. The last syntax is more robust because the type is determined by the function. Besides, this syntax returns a TermVector that may be straight exported to a file for visualization.

Note that, integral representations may return a vector of vectors but not a vector of matrices. For instance, if you want to compute the gradient of the integral representation (scalar), write:

Vector<Vector<Complex> > gsl;
integralRepresentation(xs, intg(Gamma, grad_x(K)*u, _method=ims), dnU, gsl);

or

Unknown us(V, _name="us", _dim=2); //vector unknown !
TermVector gSL=integralRepresentation(us, omega, intg(Gamma,grad_x(K)*u, _method=ims), dnU);

In this last form, attach to your TermVector a vector unknown with the dimension of the result.

Matrix method#

There exists another way to deal with integral representations. It consists in computing the matrix

\[\DeclareMathOperator{\opk}{opk} \DeclareMathOperator{\opu}{opu} R_{i,j} = \int_{\Gamma} \opk\left( G(x_i,y)\right) \otimes \opu\left(\tau_j(y) \right)\; dy.\]

Special functions will produce such matrices embedded in a TermMatrix object:

TermMatrix integralRepresentation(const Unknown&, const GeomDomain&, const LinearForm&);
TermMatrix integralRepresentation(const GeomDomain&, const LinearForm&);
TermMatrix integralRepresentation(const std::vector<Point>&, const LinearForm&);

When no domain is explicitly passed, one shadow PointsDomain object will be created from the list of points given. When no unknown is explicitly passed, one (minimal) space and related shadow unknown will be created to represent the row unknown. The following example (2D diffraction problem) shows how to use this method of integral representation:

Number nmesh=25;
Disk disk_int(_center=Point(0.,0.,0.), _radius=1., _nnodes=nmesh, _side_names="Gamma");
Disk disk_ext(_center=Point(0.,0.,0.), _radius=2., _nnodes=2*nmesh, _domain_name="Omega", _side_names="Sigma");
Mesh mesh(disk_ext-disk_int, _generator=gmsh);
Domain Gamma = mesh.domain("Gamma"), Sigma = mesh.domain("Sigma"), Omega=mesh.domain("Omega");
// define spaces, unknown and testfunction
Space V0(_domain=Gamma, _interpolation=P0, _name="V0", _notOptimizeNumbering);
Unknown u0(V0,"u0"); TestFunction v0(u0,"v0");
Space V1(_domain=Omega, _interpolation=P1, _name="V1", _notOptimizeNumbering);
Unknown u(V1,"u");
//define Kernel and integration method
Kernel H=Helmholtz3dKernel(k);
IntegrationMethods ims(_method=Duffy, _order=8, _bound=0., _quad=GaussLegendre, _order=6, _bound=2., _quad=GaussLegendre, _order=3);
//define forms
LinearForm lf = intg(Gamma, g*v0); //rhs linear form
BilinearForm aSL=intg(Gamma, Gamma, u0*H*v0, _method=ims); //single layer bininear form
LinearForm lSL(intg(Gamma, H*u0, _quad=GaussLegendre, _order=6)); //intg. rep. linear form
//build system and solve it
TermVector rhs(lf);
TermMatrix ASL(aSL);
TermVector uSL = gmresSolve(ASL, rhs, _tolerance=1.0e-6, _maxIt=500);
//intg rep on Omega producing a TermMatrix
TermMatrix R=integralRepresentation(u, Omega, lSL);
TermVector U=R*uSL;

This method is a little more time expensive than computing directly the integral representation. Thus, if there are a lot of integral representations to do with different data, it may be of interest. Obviously, it is memory consuming.

Kernel interpolation method#

When points \(x\) are far from boundary \(\Gamma\), an alternate method consists in computing IR by interpolation method. Let \(\Omega\) the domain where IR is evaluated and \(V_{\Omega}\) a Lagrange finite element space of interpolation defined on \(\Omega\). Denote \((w_i)_i\) the basis functions associated to \(V_{\Omega}\) space. Let \(W_{\Gamma}\) a Lagrange finite element space defined on \(\Gamma\) and \((\tau_j)_j\) the basis functions associated to it. Interpolated the kernel at nodes \(x_i \in \Omega\) and \(y_j \in \Gamma\), IR is approximated by

\[u(x_i) \approx \int_{\Gamma} \sum_i \sum_j G(x_i, y_j) w_i(x) \tau_j(y)q(y)\; dydx\]

If \(q\) has the following decomposition \(q(y)=\sum_k q_k \sigma_k (y)\) we have :

\[u(x_i) \approx \sum_i \sum_j \sum_k G(x_i, y_j) w_i(x) q_k \int_{\Gamma} \tau_j (y) \sigma_k(y)\; dydx\]

that reads in vector form \(\left( U = (u(x_i)_i),\;\; Q = (q(x_k)_k)\right)\):

\[U = \mathbb G * \mathbb M * q\]

with \(\mathbb G\) the matrix \(\left( G(x_i, y_j) \right)_{ij}\) and \(\mathbb M\) the mass matrix:

\[\mathbb M_{jk} = \int_{\Gamma} \tau_j \sigma_k.\]

This example shows how it is done with XLiFE++:

Space Vq(_domain=Omega, _interpolation=P0); Unknown q(Vq,"q");
//computation of Q ...
Space Vo(_domain=Omega, _interpolation=P1); Unknown u(Vo,"u");
Space Vg(_domain=Gamma, _interpolation=P1); Unknown v(Vg,"v");
TermMatrix Gi(u, Omega, v, Gamma, G, _name="Gi"); //G(xi,yj)
TermMatrix M(intg(Gamma, q*v), _name="M");
TermVector U=Gi*(M*Q);

Because kernel is interpolated, the mesh of \(\Omega\) does not be too coarse. \(Vg\) may be chosen equal to \(Vq.\) This method is generally faster than previous ones because computation of the mass matrix is a fast process, but interpolation method fails at points \(x_j\) too close to the boundary \(\Gamma\).

Visualization#

By itself, XLiFE++ is a finite element library and as such does not own any graphical possibilities. At present, three main software products are targeted through the ouput formats mentionned in the previous section.

From a practical point of view, in order to obtain a graphical representation of the computation result, one has to process the output file produced by the saveToFile command by the corresponding software. Minimal knowledge is required in order to use Gmsh and Paraview. We invite the user to refer to the documentation of these software products. Most of the computation results shown is this documentation are produced by Paraview and most of the meshes are displayed using Gmsh.

The Matlab/Octave format is intended to be (easily) used as follows. We assume we have a .m script file, say eigs_1_Omega.m, containing the first vector computed and related to the domain Omega (maybe an eigenvector or the solution to a linear system, stored as a TermVector object in both cases). One has to launch Matlab or Octave, eventually change to the directory containing the .m file and type in eigs_1_Omega at the prompt (the execution of the script can also be achieved using the menus if the GUI is available). We thus automatically get several figures, one showing the mesh based on the interpolation nodes, and one for each component of each unknown. The user is then free to make further computations using the data present in memory (see below) or modify the attributes of the figures.

The curves gathered on the figure Fig. 55 are obtained via this procedure. The corresponding mesh is :

Sy1_OmegaFig1

Fig. 56 Computational domain \([0; \pi]\)#

Another example with a 2D geometry is shown on this figure:

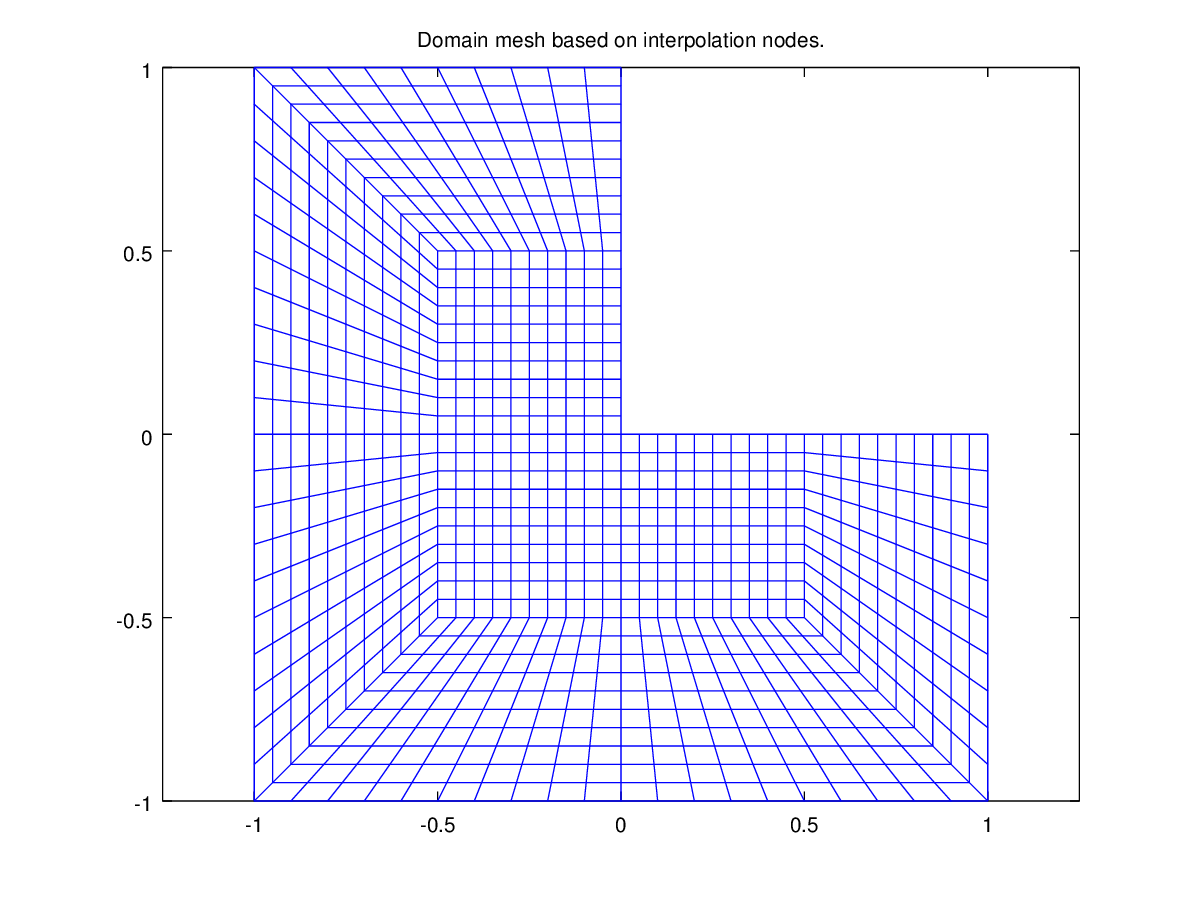
Domain mesh based on interpolation nodes Domain mesh based on interpolation nodes
eigs_2_Omega, eigvec_u, lambda_2=0;0891 eigs_2_Omega, eigvec_u, lambda_2=0;0891

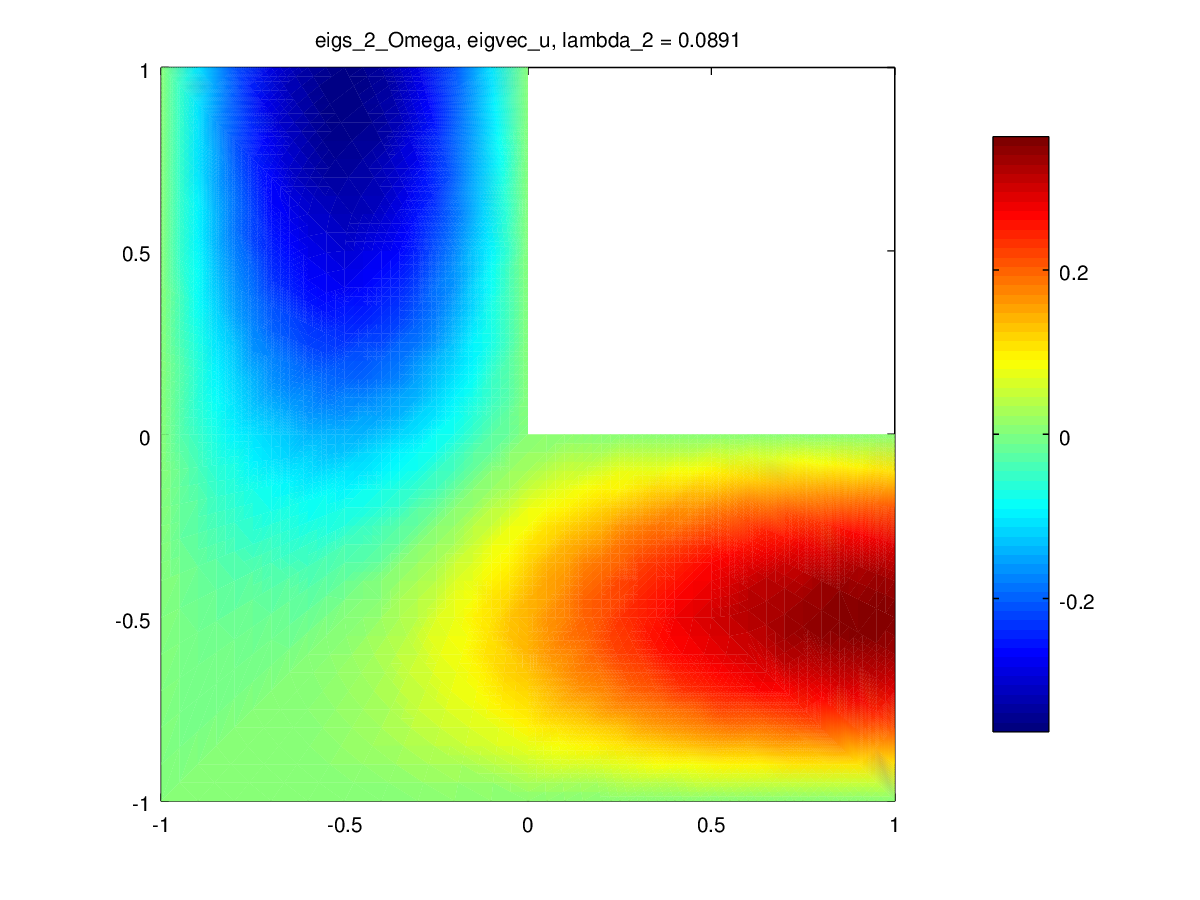
Fig. 57 A 2D example#

The script is not interactive except for volumic data: the visualization is made by slicing the 3D domain with a plane and the user is invited to choose the cutting plane defined by a point and a vector normal to the plane, shown by a red thick line on the mesh figure. The position of the cutting plane is updated on this figure as its definition changes and the corresponding slices are displayed in other figures.

Let’s show what the command window looks like in such a case, here with Octave:

GNU Octave, version 4.0.3
Copyright (C) 2016 John W. Eaton and others.
This is free software; see the source code for copying conditions.
...

>> what
M-files in directory /tmp/demo/xlifepp:

eigs_1_Omega.m
>>
>> eigs_1_Omega
The intersection plane is defined by the point P and the orthogonal vector V.

Current value of P = 12.566 12.566 12.566
Current value of V = 1 -1 0
1 : change P
2 : change V
0 : quit
Your choice (other value = no change) : 3

Current value of P = 12.566 12.566 12.566
Current value of V = 1 -1 0
1 : change P
2 : change V
0 : quit
Your choice (other value = no change) : 0
Tuning suggestions:
figure(N)
subplot(2,2,k)
rotate3d, grid, box
view(2), view(3), view([Nx Ny Nz])
shading faceted
axis equal, axis normal
set(gca,"xtick",[]) or set(gca,"xtick",[...])
caxis([...])
xlabel(...), ylabel(...), title(...)
print("-dpng",eigs_1_OmegaFig2.png)
>>

Before the user types in 3 to answer the first question, the figure showing the domain mesh and an initial cutting plane has been displayed. By choosing the value 3, the user accepts the current settings and the figure representing the field is drawn. The user then terminates by answering 0, and some hints to modify the aspect of the figures are displayed.

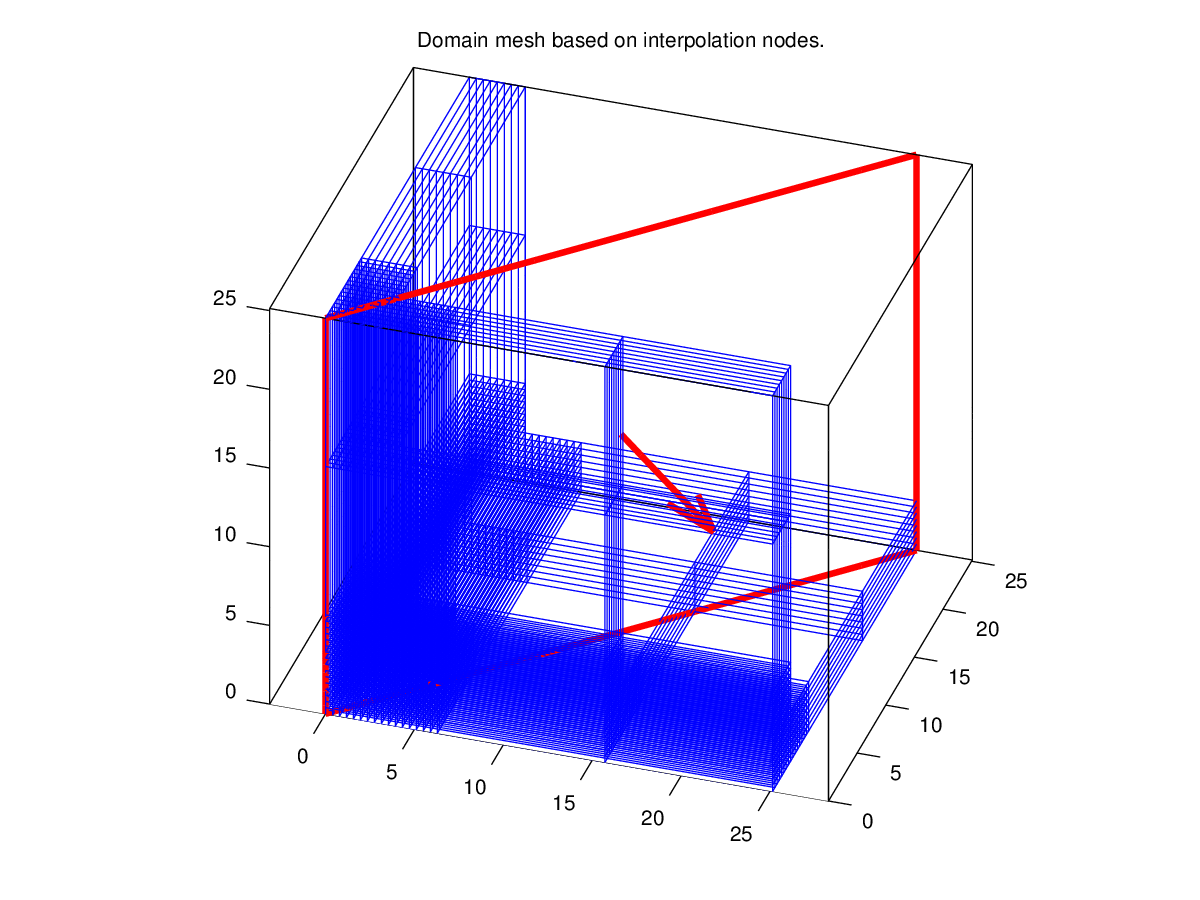
Computational domain Omega. Computational domain Omega.
Data representation corresponding to the selected slice. Data representation corresponding to the selected slice.

When the script has terminated, we can observe the variables present in the workspace:

>> whos
Variables in the current scope:

Attr Name Size Bytes Class
==== ==== ==== ===== =====
coord 5859x3 140616 double
domaindim 1x1 8 double
domainname 1x5 5 char
elem 4832x8 309248 double
elemtype 4832x1 38656 double
interpDeg 1x1 8 double
spacedim 1x1 8 double
unknown 1x8 8 char
val 5859x1 46872 double

Total is 66940 elements using 535429 bytes

>> quit

This allows the user to make any processing of his own with these data. The definitions of the variables are the following:

  • coord (real) Coordinates of the interpolation nodes, one node per row. The nodes are implicitly numbered from 1 to size(coord,1) .

  • domaindim (integer) Dimension of the domain (1, 2 or 3).

  • domainname (string) Name of the domain.

  • elem (integer) Array containing the lists of elements: elem(i,:) is an element of type elemtype(i). Format of the array: one element per row, column i holds the i-th interpolation node, given by its number in the array coord above.

  • elemtype (integer) Vector containing the type of each element present in the mesh, in the same order as the array elem above. Each type is a code number in XLiFE++’s internal codification: 2 = point, 3 = segment, 4 = triangle, 5 = quadrangle, 6 = tetrahedron, 7 = hexahedron, 8 = prism, 9 = pyramid.

  • interpDeg (integer) Interpolation degree used during the computation.

  • spacedim (integer) Dimension of the space (1, 2 or 3).

  • unknown (string) 1-column array containing the name of the unknowns, or their components in the vector case, one name per row.

  • val (real or complex) Values corresponding to the unknowns, stored column-wise, one column per component unknown. Each row contains the value at a node, or in an element if the interpolation degree is 0, in the same order as the array coord or elem respectively. Indeed, the graphical function ’patch’ used, makes the correspondence according to the number of rows of this array, which should be size(coord,1) or size(elem,1) respectively.

  • rootfn (string) Filename of the calling script.

The variables domaindim , domainname , interpDeg and spacedim are defined for information or consistency check purpose. Indeed, spacedim should equal size(coord,2) and domaindim should be less or equal spacedim and be consistent with the element types.