3D Maxwell equations using Nedelec elements

Keywords: PDE:Maxwell Method:FEM FE:Nedelec Condition:Dirichlet Solver:Direct

Dealing with 3D Maxwell problem using Nedelec elements is very similar to the 2D case. We consider the academic Maxwell problem:

\[\DeclareMathOperator{\curl}{curl} \curl \curl \mathbf{E} - \omega^2 \mu \varepsilon \mathbf{E} = \mathbf{f} \quad \mathrm{in\;}\Omega\]

equipped with the natural boundary condition:

\[\DeclareMathOperator{\curl}{curl} \curl \mathbf{E} \times n = \mathbf{g} \quad \mathrm{on\;} \partial \Omega.\]

The variational formulation in \(V=H(curl,\Omega)\}\) is to find:

\[\DeclareMathOperator{\curl}{curl} \mathbf{E} \in V \mid \forall \mathbf{v} \in V, \int_\Omega \curl \mathbf{E} \cdot \curl \mathbf{v} - \omega^2 \mu \varepsilon \int_\Omega \mathbf{E} \cdot \mathbf{v} = \int_\Omega \mathbf{f} \cdot \mathbf{v} + \int_{\partial \Omega} \mathbf{g} \cdot \mathbf{v}\]

In the example we use as a solution

\[\begin{split}\mathbf{E}_{ex}(x,y,z) = \begin{pmatrix} -2\cos(a x)\sin(a y)\sin(a z) \\ \sin(a x)\cos(a y)\sin(a z) \\ \sin(a x)\sin(a y)\cos(a z) \end{pmatrix}\end{split}\]

with \(\DeclareMathOperator{\curl}{curl} \mathbf{f}=\curl \curl \mathbf{E}_{ex} - \omega^2 \mu \varepsilon \mathbf{E}_{ex}\) and \(\DeclareMathOperator{\curl}{curl} \mathbf{g}=\curl \mathbf{E}_{ex}\times n\).

Using the first family Nedelec’s elements, the XLiFE++ program looks like:

#include "xlife++.h"
using namespace xlifepp;

Real omg=1, eps=1, mu=1, a=pi_, ome=omg* omg* mu* eps;

Vector<Real> f(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), y=P(2), z=P(3);
  Vector<Real> res(3);
  Real c=3*a*a-ome;
  res(1)=-2*cos(a*x)*sin(a*y)*sin(a*z)*c;
  res(2)=   sin(a*x)*cos(a*y)*sin(a*z)*c;
  res(3)=   sin(a*x)*sin(a*y)*cos(a*z)*c;
  return res;
}

Vector<Real> fg(const Point& P, Parameters& pa = defaultParameters)  // rot u
{
  Real x=P(1), y=P(2), z=P(3);
  Vector<Real> res(3);
  res(1)= 0.;
  res(2)=-3*a*cos(a*x)*sin(a*y)*cos(a*z);
  res(3)= 3*a*cos(a*x)*cos(a*y)*sin(a*z);
  Vector<real_t>& n=getN();
  return crossProduct(res,n);
}

Vector<Real> solex(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), y=P(2), z=P(3);
  Vector<Real> res(3);
  res(1)=-2*cos(a*x)*sin(a*y)*sin(a*z);
  res(2)=   sin(a*x)*cos(a*y)*sin(a*z);
  res(3)=   sin(a*x)*sin(a*y)*cos(a*z);
  return res;
}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en);
  // mesh cube using gmsh
  Cube cu(_origin=Point(0.,0.,0.), _length=1.,_nnodes=11, _domain_name="Omega", _side_names="Gamma");
  Mesh mesh3d(cu, _shape=tetrahedron, _generator=gmsh, _name="mesh of the unit cube");
  Domain omega=mesh3d.domain("Omega"), gamma=mesh3d.domain("Gamma");
  // define space and unknown
  Space V(_domain=omega,_interpolation=N1_1,_name="V",_notOptimizeNumbering);
  Unknown e(V, _name="E"); TestFunction q(e, _name="q");
  // define forms
  BilinearForm aev=intg(omega,curl(e)|curl(q))-ome*intg(omega,e|q);
  LinearForm lf=intg(omega,f|q);
  Function g(fg); g.require(_n);
  LinearForm lg=intg(gamma,g|q);
  // compute matrix and vector 
  TermMatrix A(aev, _name="A");
  TermVector b = TermVector(lf)+ TermVector(lg);
  // solve system
  TermVector E=directSolve(A, b);
  
  // L2 projection on P1 FE
  Space W(_domain=omega, _interpolation=P1, _name="W");
  TermVector EP1=projection(E, W, 3);
  saveToFile("E.vtu", EP1, _data_name="E");
  // interpolation on P1 mesh
  Unknown u(W, _name="u", _dim=3);
  TermVector Ei=interpolate(u,omega,E,"Ei");
  saveToFile("Ei", Ei, _format=vtu);
  return 0;
}

As Nedelec finite elements approximation are not conforming in \(H^1(\Omega)\), the solution is not continuous across elements (only tangent component is continuous). So to represent the solution, it is projected on \(H^1(\Omega)\) as follows, by finding:

\[\mathbf{E}_1 \in \left(H^1(\Omega)\right)^n \mid \forall \mathbf{w}\in \left(L^2(\Omega)\right))^n, \int_{\Omega}\mathbf{E}_1\,\mathbf{w}=\int_{\Omega}\mathbf{E}\,\mathbf{w} \qquad n= \dim \Omega\]

Using an H1 conforming approximation for \(\mathbf{E}_1\) leads to a continuous representation of the projection. We show on the next figure the module of the field \(E\) provided by this example:

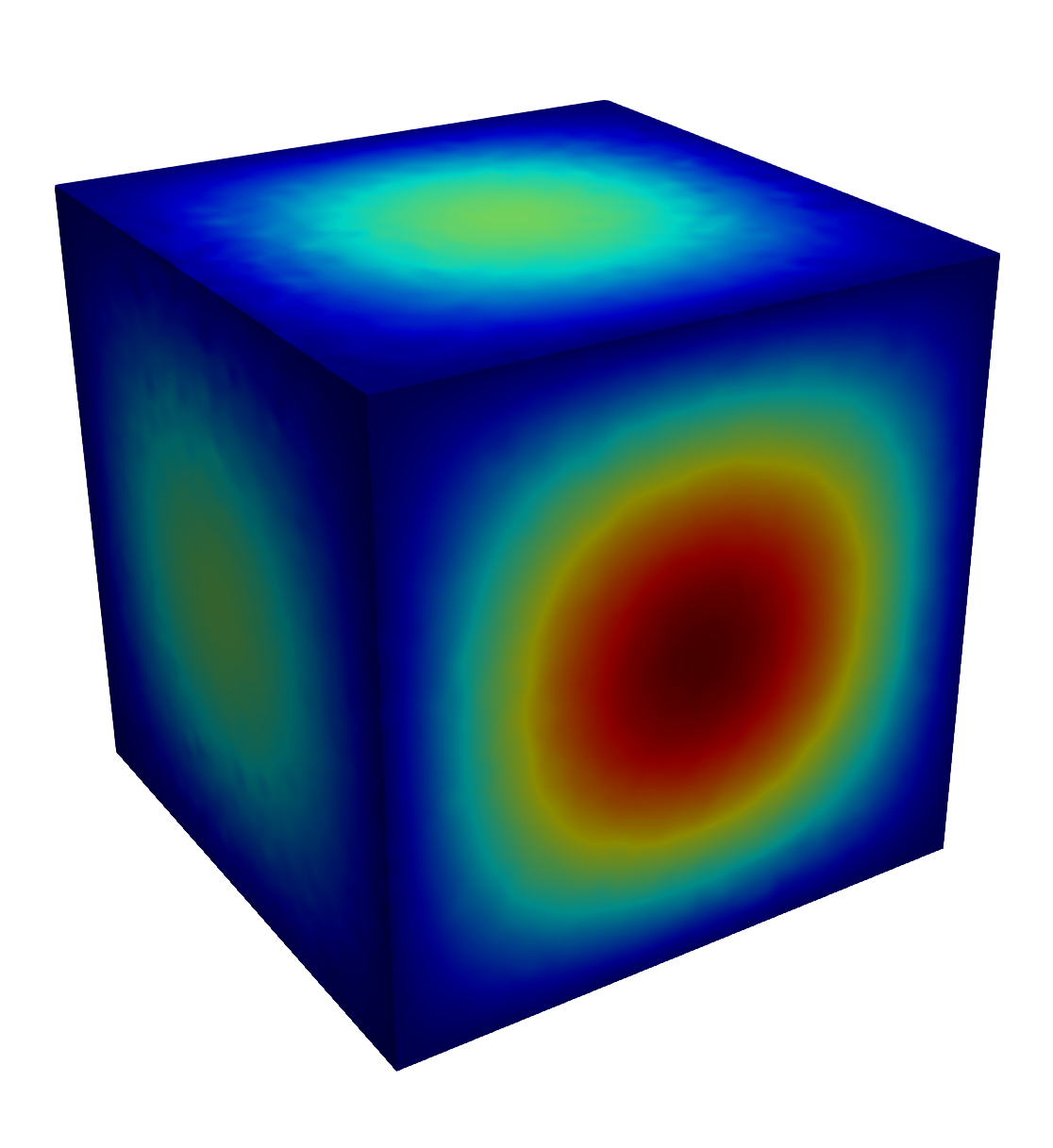
Fig. 9 Module of the solution of the Maxwell 3D problem using Nedelec first family elements

Alternatively, the interpolate() function provides the interpolation of \(E\) on nodes of a P1 approximation.

On the next figure, the convergence curve shows a rate convergence of \(L^2\) error in \(h^{1.3}\) :

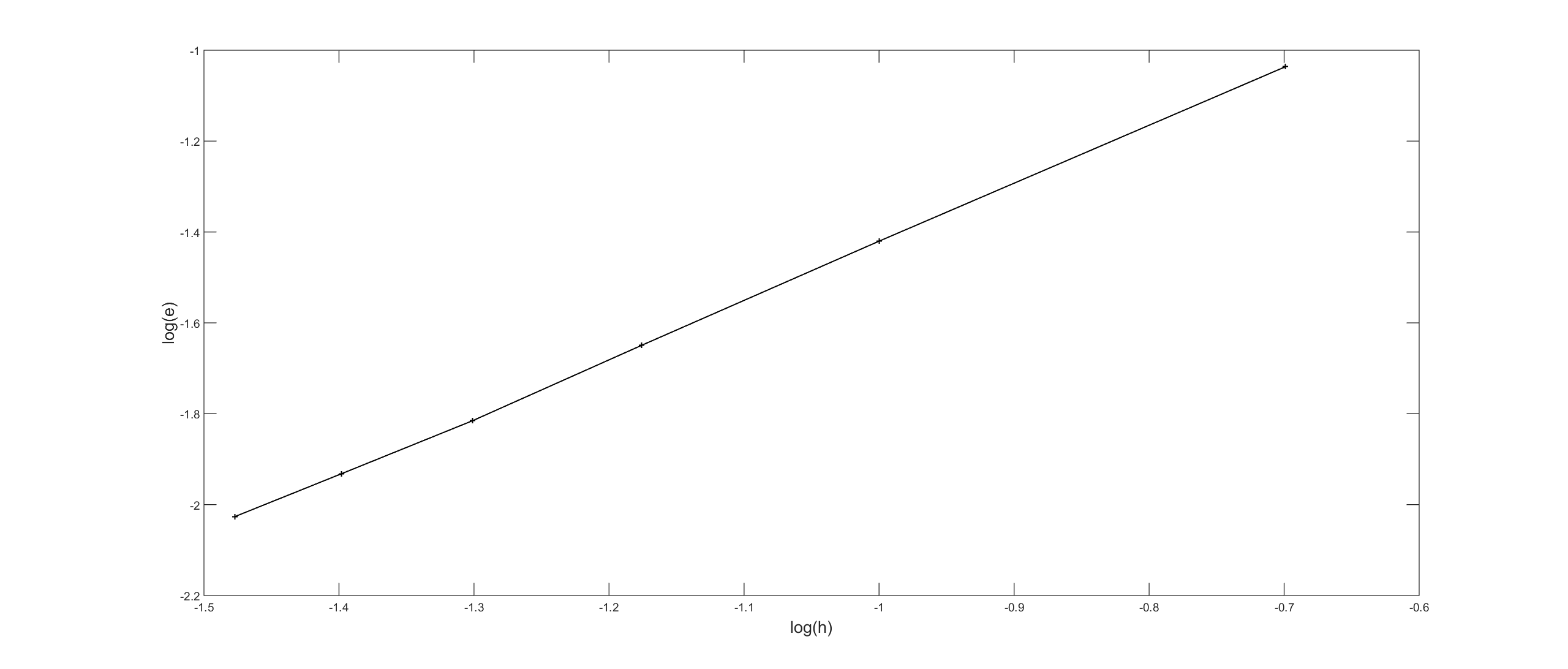
Fig. 10 \(L^2\) errors versus the step \(h\) for first order Nedelec first family approximation