2D Helmholtz problem coupling FEM and integral representation

Keywords: PDE:Helmholtz Method:FEM Method:Coupling FE:Lagrange Solver:Direct

We want to solve the acoustic diffraction of a plane wave on the disk of radius 1, with the boundary \(\Gamma\):

\[\begin{split}\begin{cases} \Delta u + k^2u= 0 & \mathrm{\;in\;}\mathbb{R}^2/D \\ \partial_nu = g & \mathrm{\;on\;}\Gamma\ (n \mathrm{\;the\;outward\;normal}) \end{cases}\end{split}\]

where \(g=\partial_n\left( e^{ikx}\right)\).

Let \(\Omega\) be a domain that strictly surrounding the disk D and \(\Sigma\) its boundary. We have to point out that in this case, we use normals going outside the domain of computation \(\Omega\) but then the normal on the obstacle (defined on \(\Gamma\)) is going inside the obstacle, that is opposite to usual case (see figure below). Then, because of the normal inverted, the solution \(u\) may be represented by the integral representation formula (\(G\) is the Green function related to the 2D Helmholtz equation in free space):

(1)\[\forall x\in \Sigma,\ \ u(x)=-\int_{\Gamma}\partial_{n_y}G(x,y)\,u(y)\,dy+ \int_{\Gamma}G(x,y)\,\partial_{n_y}u(y)\,dy\]

say, because the boundary condition:

\[u(x)=-\int_{\Gamma}\partial_{n_y}G(x,y)\,u(y)\,dy+ \int_{\Gamma}G(x,y)\,g(y)\,dy.\]

\(n_y\) is the outward normal (to \(\Omega\) not the obstacle) on \(\Gamma\) and \(n_x\) will denote the outward normal on \(\Sigma\). Now matching values and normal derivative on \(\Sigma\), we introduce the boundary condition:

\[(\partial_{n_x}+\lambda)u(x) = -(\partial_{n_x}+\lambda)\int_{\Gamma}\partial_{n_y}G(x,y)\,u(y)\,dy +(\partial_{n_x}+\lambda)\int_{\Gamma}G(x,y)\,g(y)\,dy\]

that reads, because \(G\) is not singular on \(\Gamma\times\Sigma\):

\[\begin{split}\begin{array}{rl} (\partial_{n_x}+\lambda)u(x) = &\displaystyle -\int_{\Gamma}\partial_{n_x}\partial_{n_y}G(x,y)\,u(y)\,dy -\lambda\int_{\Gamma}\partial_{n_y}G(x,y)\,u(y)\,dy\\ + &\displaystyle \int_{\Gamma}\partial_{n_x}G(x,y)\,g(y)\,dy +\lambda\int_{\Gamma}G(x,y)\,g(y)\,dy = \mathcal{R}_\lambda(u)(x) \end{array}\end{split}\]

Using this exact boundary condition, if \(Im(\lambda)\neq 0)\) the initial problem is equivalent to:

\[\begin{split}\begin{cases} \Delta u + k^2u= 0 & \mathrm{\;in\;}\Omega \\ \partial_nu = g & \mathrm{\;on\;}\Gamma\\ (\partial_{n_x}+\lambda)u = \mathcal{R}_\lambda(u) & \mathrm{\;on\;}\Sigma \end{cases}\end{split}\]

Its variational formulation in \(V=H^1(\Omega)\) is:

\[\begin{split}\left| \begin{array}{c} \mathrm{find\;} u\in V \mathrm{\;such\;that\;} \forall v\in V \\ \displaystyle \int_\Omega \nabla u.\nabla \bar{v} - k^2\int_\Omega u\, \bar{v} + \lambda\int_{\Sigma}u\,\bar{v} +\int_\Sigma\int_{\Gamma} u(y)\partial_{n_x}\partial_{n_y}G(x,y)\,\bar{v}(x) +\lambda\int_\Sigma\int_{\Gamma} u(y)\partial_{n_y}G(x,y)\,\bar{v}(x) \\ \hfill \displaystyle =\int_\Gamma g\,\bar{v}+\int_\Sigma\int_{\Gamma} g(y)\partial_{n_x}G(x,y)\,\bar{v}(x)+\lambda\int_\Sigma\int_{\Gamma} g(y)G(x,y)\,\bar{v}(x). \end{array} \right.\end{split}\]

Considering the geometrical configuration:

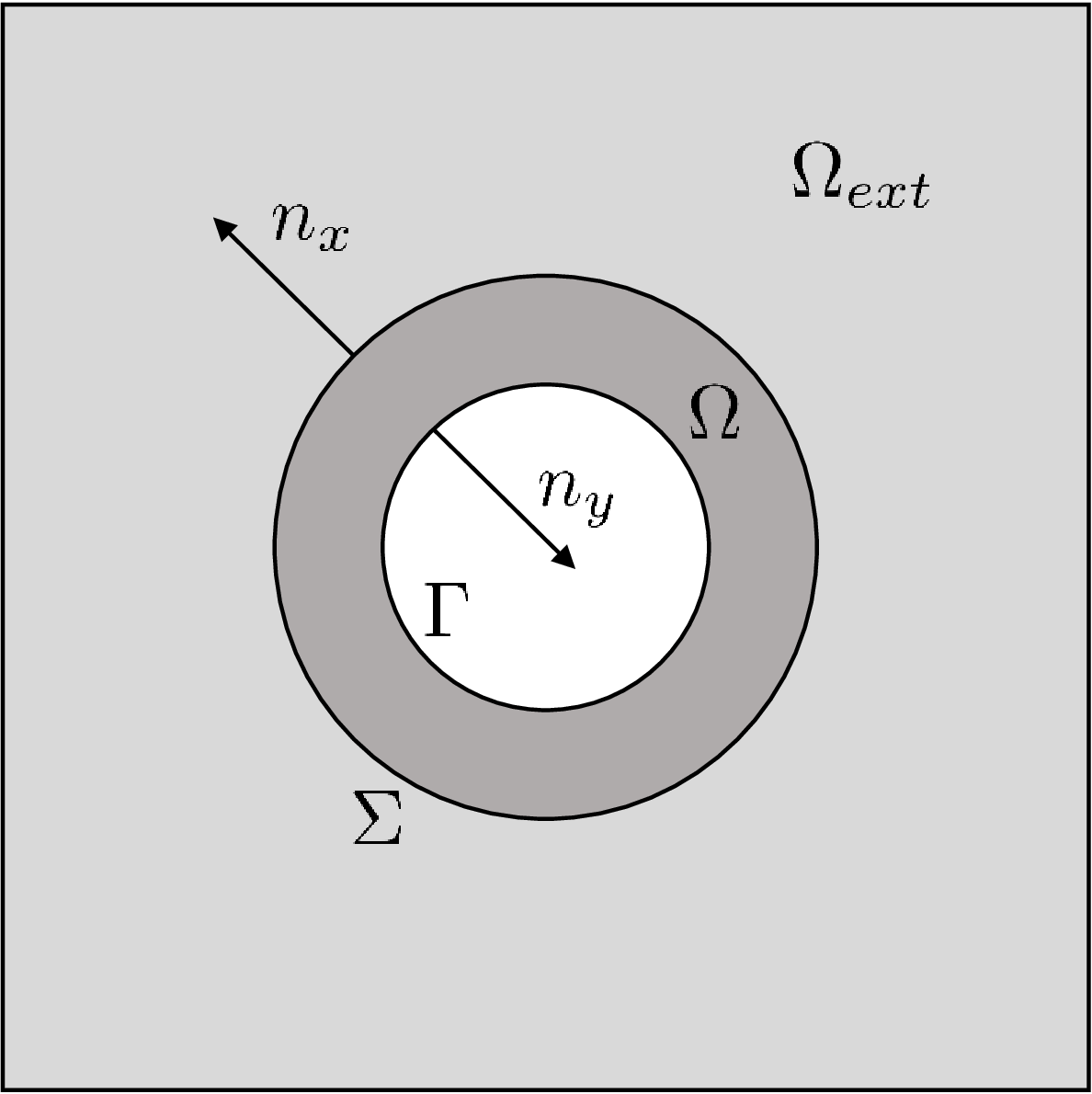
Fig. 21 Geometrical configuration for the FEM-Integral Representation problem. The normal on \(\Gamma\) is going inside the obstacle (to point outside \(\Omega\)).

The variational formulation is implemented as follows:

#include "xlife++.h"
using namespace xlifepp;

Complex data_g(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), k=pa("k");
  Vector<Complex> g(2, 0.);
  g(1) = i_*k*exp(i_*k*x);
  return dot(g, P/norm2(P));  //dr(e^{ikx}
}

Complex u_inc(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), k=pa("k");
  return exp(i_*k*x);
}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp
  //parameters
  Number nh = 10;               // number of elements on Gamma
  Real h=2*pi_/nh;              // size of mesh
  Real re=1.+2*h;               // exterior radius
  Number ne=Number(2*pi_*re/h); // number of elements on Sigma
  Real l = 4*re;                // length of exterior square
  Number nr=Number(4*l/h);      // number of elements on exterior square
  Real k= 4, k2=k*k;            // wavenumber
  Parameters pars;
  pars << Parameter(k, "k") << Parameter(k2, "k2");
  Kernel H=Helmholtz2dKernel(pars);
  Function g(data_g, pars);
  Function ui(u_inc, pars);
  //Mesh and domains definition
  Disk d1(_center=Point(0., 0.), _radius=1, _nnodes=nh, _side_names=Strings(4, "Gamma"));
  Disk d2(_center=Point(0., 0.), _radius=re, _nnodes=ne, _domain_name="Omega", _side_names=Strings(4, "Sigma"));
  SquareGeo sq(_center=Point(0., 0.), _length=l, _nnodes=nr, _domain_name="Omega_ext");
  Mesh mesh(sq+(d2-d1), _shape=triangle, _generator=gmsh);
  Domain omega=mesh.domain("Omega");
  Domain sigma=mesh.domain("Sigma");
  Domain gamma=mesh.domain("Gamma");
  Domain omega_ext=mesh.domain("Omega_ext");  //for integral representation
  sigma.setNormalOrientation(_outwardsDomain, omega); //outwards normals
  gamma.setNormalOrientation(_outwardsDomain, omega);

  //create P2 Lagrange interpolation
  Space V(_domain=omega, _interpolation=P2, _name="V");
  Unknown u(V, _name="u");  TestFunction v(u, _name="v");
  // create bilinear form and linear form
  Complex lambda=-i_*k;
  BilinearForm auv = intg(omega, grad(u)|grad(v))-k2*intg(omega, u*v)+lambda*intg(sigma, u*v)
                     + intg(sigma, gamma, u*(grad_y(grad_x(H)|_nx)|_ny)*v)
                     + lambda*intg(sigma, gamma, u*(grad_y(H)|_ny)*v);
  BilinearForm alv = intg(sigma, gamma, u*(grad_x(H)|_nx)*v)+lambda*intg(sigma, gamma, u*H*v);
  TermMatrix A(auv), ALV(alv);
  TermVector B(intg(gamma, g*v));
  TermVector G(u, gamma, g);
  B+=ALV*G;
  //solve linear system AU=F
  TermVector U=directSolve(A, B);
  saveToFile("U.vtk", U);
  //integral representation on omega_ext
  Space Vext(_domain=omega_ext, _interpolation=P2, _name="Vext", _notOptimizeNumbering);
  Unknown uext(Vext, _name="uext");
  TermVector Uext = - integralRepresentation(uext, omega_ext, intg(gamma, (grad_y(H)|_ny)*U))
                    + integralRepresentation(uext, omega_ext, intg(gamma, H*G));
  saveToFile("Uext.vtk", Uext);
  //total field
  TermVector Ui(u, omega, ui), Utot=Ui+U;
  TermVector Uiext(uext, omega_ext, ui), Utotext=Uiext+Uext;
  saveToFile("Utot.vtk", Utot);
  saveToFile("Utotext.vtk", Utotext);
  return 0;
}

In the beginning, some geometric parameters used to design crown surrounded by a square, are given. Next the mesh is generated using gmsh mode and the geometrical domains are got from the mesh. The normal orientations are chosen in order to have outwards normals to the crown omega.

Then a P2 Lagrange space over the elements of the crown omega is constructed and all bilinear and linear forms involved in variational form are defined. Then the TermMatrix and TermVector are computed, and the problem is solved using a direct method (Umfpack if it is installed, LU factorization else), that leads to the solution U in the crown omega.

Finally, using integral representation formula (), the solution is computed in the exterior domain omega_ext. The vectors U and Uext are diffracted fields. To get total field, the incident field has to be added to the diffracted field. This is the final job that it is done.

The real part of the total field computed is presented on the following figure:

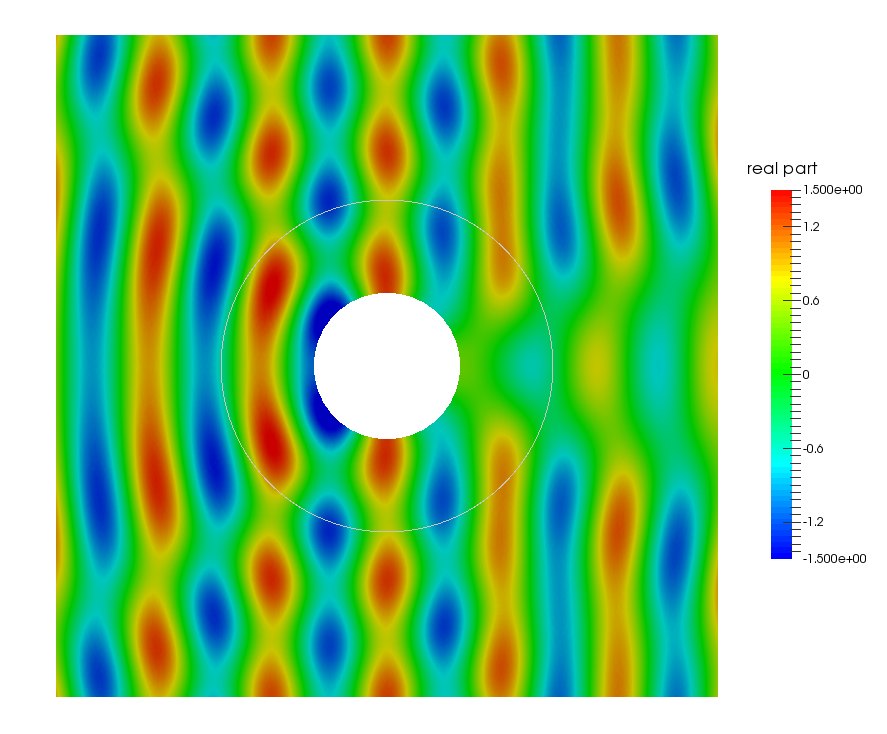
Fig. 22 2D Helmholtz diffraction problem using FE-IR method: real part of the total field