2D Bilaplacian problem

Keywords: PDE:Bilaplacian Method:FEM FE:Morley Solver:Direct

The 2d bilaplacian problem illustrates how to use Morley or Argyris element in XLiFE++:

\[\begin{split}\begin{cases} \Delta^2 u= \mathbf{f} & \mathrm{\;in\;}\Omega \\ u=0 \mathrm{\;and\;} \nabla u.\mathbf{n}=0 & \mathrm{\;on\;}\partial \Omega \end{cases}\end{split}\]

The variational formulation in \(V=\big\{v\in H^2(\Omega),\ u=0\mathrm{\;and\;} \nabla u.n=0\mathrm{\;on\;}\partial \Omega\big\}\) is:

\[\begin{split}\left|\begin{array}{l} \mathrm{find\;}\mathbf{u}\in V \mathrm{\;such\;that\;} \\ \displaystyle \int_\Omega\left(\partial_{xx} u \partial_{xx} v + \partial_{yy} u \partial_{yy} v + 2\partial_{xy} u \partial_{xy} v \right)=\int_\Omega f v \quad \forall \mathbf{v}\in V. \end{array}\right.\end{split}\]

The implementation in XLiFE++ using Morley elements is the following:

#include "xlife++.h"
using namespace xlifepp;

// data function
Real uex(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), y=P(2), kp=pi_;
  Real r=sin(kp*x)*sin(kp*y);
  return r*r;
}

Real f(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), y=P(2);
  Real dkp=2*k*pi_;
  Real cx=cos(dkp*x), cy=cos(dkp*y);
  return 0.25*dkp*dkp*dkp*dkp*(4*cx*cy-cx-cy);
}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp
  // mesh rectangle
  SquareGeo sq(_xmin=0, _xmax=1, _ymin=0, _ymax=1., _hsteps=0.05, _domain_name="Omega", _side_names="Gamma");
  Mesh mesh(sq, _shape=triangle, _generator=gmsh);
  Domain omega=mesh.domain("Omega"), gamma=mesh.domain("Gamma");
  // create space
  Space V(_domain=omega, _FE_type=Morley, _order=1, _name="V");
  Unknown u(V, _name="u");  TestFunction v(u, _name="v");
  // create problem
  EssentialConditions ecs= (u|gamma = 0) & (ndotgrad(u)|gamma = 0);
  TermMatrix A(intg(omega, dxx(u)*dxx(v))+intg(omega, dyy(u)*dyy(v))+2*intg(omega, dxy(u)*dxy(v)), ecs);
  TermVector B(intg(omega, f*v), _name="B");
  // solve problem
  TermVector U=directSolve(A, B);
  // interpolate on P1 and export to vtu file
  Space W(_domain=omega, _interpolation=P1, _name="W", _notOptimizeNumbering);
  Unknown w(W, _name="w");
  TermVector Up1=interpolate(w, omega, U, "Up1");
  saveToFile("U", Up1, _format=vtu);
  TermVector Ue1(w, omega, uex, _name="Ue1");
  TermVector Er=Up1-Ue1;
  saveToFile("Er", Er, _format=vtu);
  return 0;
}

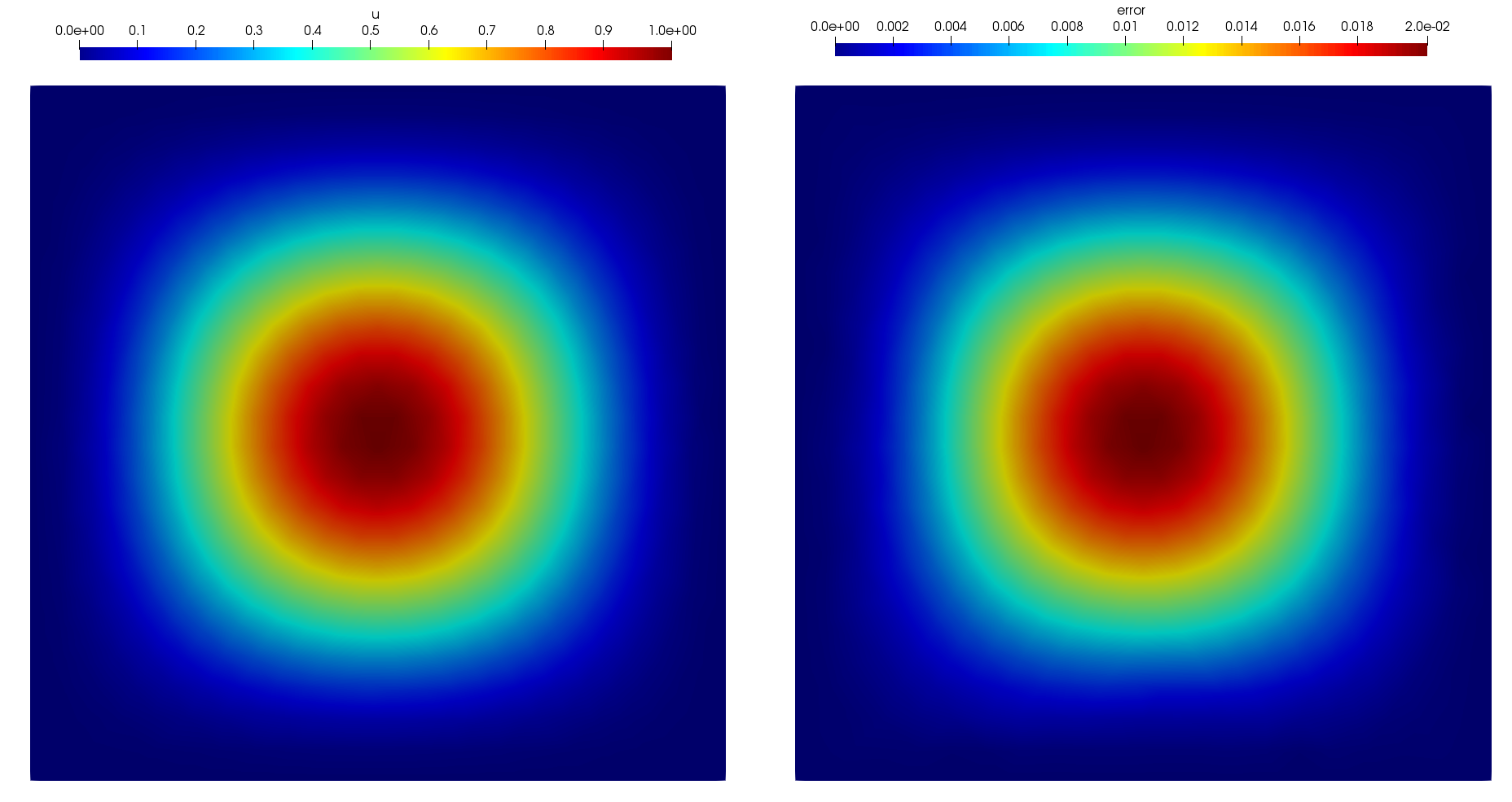
Fig. 32 Approximate solution and difference with exact solution of the bilaplacian 2D problem

In order to use Argyris element in place of Morley element, replace the space definition:

Space V(_domain=omega, _FE_type=Argyris, _order=1, _name="V");

The next figure shows the \(L^2\) convergence rate of the Morley approximation when solving the 2d bilaplacian problem; in agreement with the order 2 predicting by the theory.

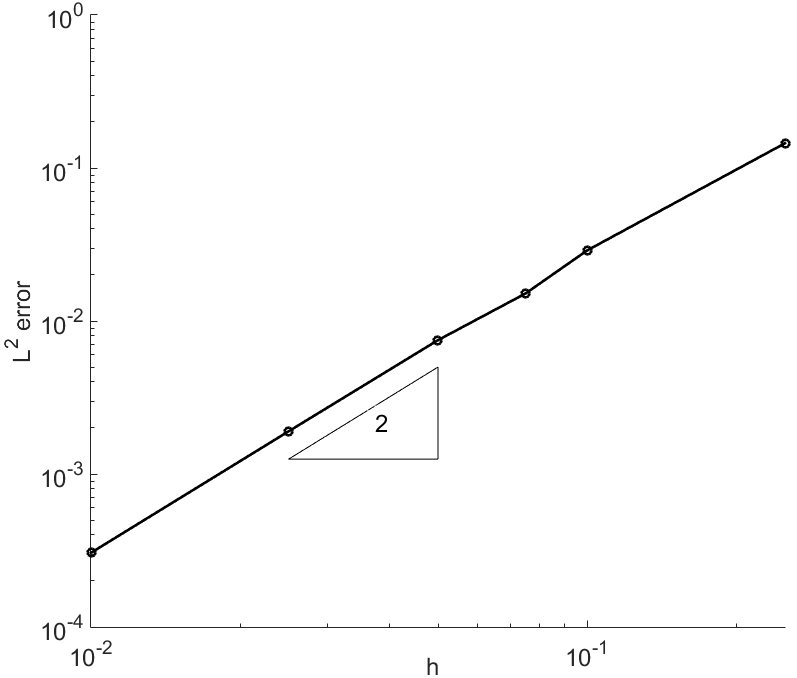
Fig. 33 \(L^2\) convergence rate of the Morley approximation