2D Stokes problem

Keywords: PDE:Stokes Method:FEM FE:CrouzeixRaviart FE:TaylorHood Condition:Dirichlet Solver:Direct

We consider the problem of a flow entrained in a cavity, say \(\Omega=]0,1[\times]0,1[\):

\[\begin{split}\DeclareMathOperator{\divop}{div} \begin{cases} -\nu\bigtriangleup \mathbf{u} + \nabla p=\mathbf{f} & \mathrm{in\;}\Omega \\ \divop \mathbf{u} = 0 & \mathrm{in\;}\Omega \\ \mathbf{u}=\mathbf{g} & \mathrm{on\;}\Sigma=\{0\}\times ]0,1[ \\ \mathbf{u}=\mathbf{0} & \mathrm{on\;}\Gamma=\partial \Omega\backslash \Sigma \end{cases}\end{split}\]

with \(\mathbf{f} \in L^2(\Omega)\) and \(\mathbf{g}=(0,v_0),\ v_0\in H^{\frac{1}{2}}_{00}(\Sigma)\). Note that \(\mathbf{g}|\mathbf{n}=0\).

This problem has the following variational formulation: find \((\mathbf{u},p)\in H^1(\Omega)^2\times L^2_0(\Omega)\) such that for all \((\mathbf{v},p)\in H^1_0(\Omega)^2\times L^2_0(\Omega)\):

\[\begin{split}\DeclareMathOperator{\divop}{div} \begin{cases} \displaystyle \nu\int_\Omega \nabla \mathbf{u}:\nabla \mathbf{v} -\int_\Omega p \divop \mathbf{v}-\int_\Omega \divop \mathbf{u} q=\int_\Omega \mathbf{f} \cdot \mathbf{v} \\ \mathbf{u}=\mathbf{g} \mathrm{\;on\;}\Sigma \mathrm{\;and\;} \mathbf{u}=\mathbf{0} \mathrm{\;on\;}\Gamma \end{cases}\end{split}\]

The following XLiFE++ implementation of this problem solves the 2D Stokes problem using different couples of approximation for the velocity \(v\) and the pressure \(p\) : (P2, P0), (P2, P1), (CR, P0); CR corresponds to a P1 Crouzeix-Raviart finite element approximation leading to a non-conforming approximation of \(H^1\). Note that the (P1, P0) approximation is not working because of dof locking.

#include "xlife++.h"
using namespace xlifepp;
using namespace std;

Vector<Real> g(const Point& p, Parameters& pa = defaultParameters)
{
    Vector<Real> r(2,0.);
    r(2)=1.;
    return r;
}

int main(int argc, char** argv)
{
  init(_lang=en); // mandatory initialization of xlifepp
  verboseLevel(1);
  //geometry data
  Square sq(_origin=Point(0.,0.),_length=1., _nnodes=30, _domain_name="Omega",
            _side_names=Strings("Gamma","Gamma", "Gamma", "Sigma"));
  Mesh mesh(sq, _shape=triangle);
  Domain Omega=mesh.domain("Omega");
  Domain Sigma=mesh.domain("Sigma");
  Domain Gamma=mesh.domain("Gamma");
  // solve Stokes 2D for several approximations
  list<pair<InterpolationType,InterpolationType>> pint={{P0,P2},{P1,P2},{P0,CR}};
  for (auto ps:pint)
  {
    Space H1(_domain=Omega,_interpolation=ps.second,_name="H1");
    Unknown u(H1,_name="u",_dim=2); TestFunction v(u,_name="v");
    Space L2(_domain=Omega,_interpolation=ps.first,_name="L2");
    Unknown p(L2,_name="p"); TestFunction q(p,_name="q");
    BilinearForm a = intg(Omega,grad(u)%grad(v))-intg(Omega,p*div(v))-intg(Omega,div(u)*q);
    EssentialConditions ecs = (u|Gamma = 0) & (u | Sigma = g) & (intg(Omega,p)=0);
    TermMatrix A(a,ecs,_name="A");
    TermVector b(u,Omega,0.,_name="b");
    TermVector X=directSolve(A,b);
    String filename=fileNameFromComponents("u", words("interpolation",ps.first)+"_"+words("interpolation",ps.second), "vtu");
    saveToFile(filename, X(p));
    if (ps.second==_CR)
    {
      Space V1(_domain=Omega,_interpolation=P1, _name="V1");
      TermVector u1=projection(X(u),V1,2);
      saveToFile(filename, u1, _data_name="u1");
    }
    else saveToFile(filename, X(u));
  }
  return 0;
}

Using Paraview with the Glyph filter that represents 2D vectors with arrows, we get the following pictures:

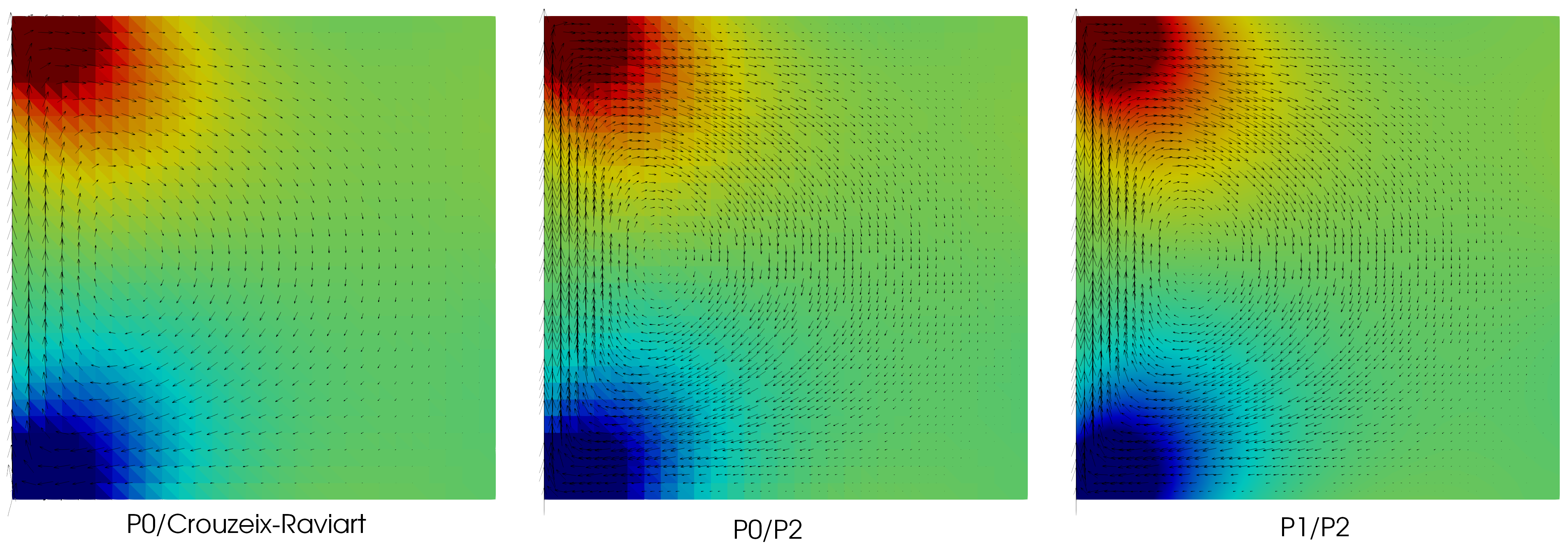
Fig. 11 Solution of the 2D Stokes problem using different approximations

Note that to approximate the space \(L^2_0(\Omega)\), an essential condition of the zero mean type of pressure p has been used. Such a condition is quite costly because it interacts with all the pressure dofs. If we remove it, the matrix becomes singular (the pressure being defined to within a constant) and direct solvers fail. But iterative solvers do converge to the right velocity, and pressure to the right constant, determined by the initial guess of the iterative solver !

Note also that, when using Crouzeix-Raviart element, in order to visualize the velocity, it is required to project the CR solution in a standard Lagrange finite element space (here \(P_1\)).