3D Maxwell equations with PML#
Now, we consider a waveguide equipped with a PML (Perfectly Matched Layer).
Just recall that such a layer allows to absorb the waves without any reflection if the layer is infinite. When the PML is bounded, there is only some weak reflections due to a reflection on the back of the PML, more and more strong as the layer becomes thin.
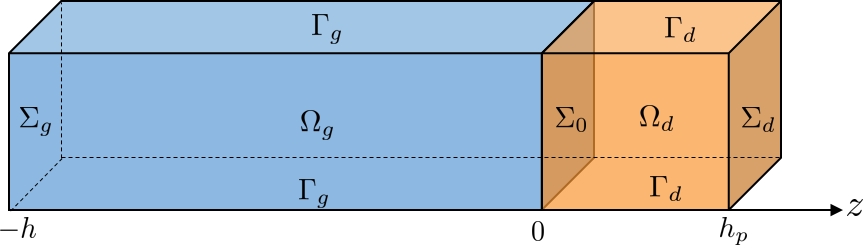
The PML mechanism consisting in dilatating one coordinate with a complex factor, we need to apply a change of unknowns to obtain the following equivalent strong formulation (\(\mu = \varepsilon=1\)):
\[\begin{split}\DeclareMathOperator{\curl}{curl}
\left\{\begin{array}{ll}
\curl \curl \mathbf{E}-\omega^2 \mathbf{E} = \mathbf{f} & \mathrm{in\;}\Omega_g \\
\curl \mathbb{A}^{-1}\curl \mathbf{E}-\omega^2 \mathbb{A}\mathbf{E} = \mathbf{O} & \mathrm{in\;}\Omega_d \quad \mathrm{(PML)}\\
\mathbf{E}\times n= g & \mathrm{on\;} \Sigma_g \\
\curl \mathbf{E}\times n= 0 & \mathrm{on\;}\Sigma_d \\
\mathbf{E}\times n= 0 & \mathrm{on\;} \Gamma_g\cup\Gamma_d \\
\left[\mathbf{E}\times n\right]_{\Sigma_0}= 0,\quad \left[\curl \mathbf{E}\times n\right]_{\Sigma_0}=0 & \mathrm{(transmission\;condition)} \\
\end{array}\right.\end{split}\]
where \(\mathbb{A}\) represents either the change of unknowns and the PML dilatation (\(\alpha\in\mathbb{C}\)):
\[\begin{split}\mathbb{A}=\left[
\begin{array} {ccc}
\frac{1}{\alpha}& 0& 0\\
0& \frac{1}{\alpha} & 0\\
0 & 0 &\alpha
\end{array}
\right].\end{split}\]
Let us introduce
\[V_g^0=\{\mathbf{v}\in H(\mathrm{curl},\Omega_g),\,\mathbf{v}\times n=0\mathrm{\;on\;}\Gamma_g\},
V_d^0=\{\mathbf{v}\in H(\mathrm{curl},\Omega_d),\,\mathbf{v}\times n=0\mathrm{\;on\;}\Gamma_d\}\]
and
\[W = \left\{(\mathbf{v_g},\mathbf{v_d})\in V^0_g\times V^0_d \mathrm{\;s.t.\;} \mathbf{v_g}\times n=\mathbf{v_d}\times n\mathrm{\;on\;}\Sigma_0 \right\}.\]
The strong formulation has the following weak form:
\[\begin{split}\DeclareMathOperator{\curl}{curl}
\left|
\begin{array}{l}
\mathrm{find\;}(\mathbf{E_g},\mathbf{E_d}) \in W \mathrm{\;such\;that\;} \mathbf{E_g}\times n=g \mathrm{\;on\;} \Sigma_g \mathrm{\;and\;} \forall (\mathbf{v_g},\mathbf{v_d}) \in W \mathrm{\;with\;} \mathbf{v_g} \times n=0 \mathrm{\;on\;} \Sigma_g:\\
\displaystyle \int_{\Omega_g} \curl \mathbf{E_g}\cdot\curl \mathbf{v_g} - \omega^2\int_{\Omega_g} \mathbf{E_g} \cdot \mathbf{v_g}
+ \int_{\Omega_d}\mathbb{A}^{-1}\curl \mathbf{E_d}\cdot\curl \mathbf{v_d} - \omega^2\int_{\Omega_d} \mathbb{A}\mathbf{E_d}\cdot\mathbf{v_d} = 0.
\end{array}
\right.\end{split}\]
Note that we have to deal with many essential conditions, in particular the transmission condition \(\mathbf{E_g}\times n=\mathbf{E_d}\times n\) on \(\Sigma_0\).
In the following example, a ‘Neumann’ mode of the wave-guide is used as exact solution. Using the first family Nedelec’s elements (NE11 or NE12) the XLiFE++ program looks like:
#include "xlife++.h"
using namespace xlifepp;
// Neumann modes and their tangential traces (n=[0 0 -1])
Vector<Complex> mode_Neumann(const Point&P,Real n,Real m,Parameters& pa=defaultParameters)
{
Real x = P(1), y = P(2), z = P(3), cst;
Real a = pa("a"), b = pa("b"), w = pa("w");
Vector<Complex> u(3);
Real lambda = pi_*pi_ * ( n*n / (a*a) + m*m / (b*b));
if ( (n == 0) || (m == 0) ) cst = sqrt(2.)/sqrt(lambda * a * b);
else cst = 2./sqrt(lambda * a * b);
Complex beta = sqrt(Complex(w*w-lambda));
u(1) = - m*pi_/b * cst * exp(i_*beta*z) * cos(n*pi_*x/a) * sin(m*pi_*y/b);
u(2) = n*pi_/a * cst * exp(i_*beta*z) * sin(n*pi_*x/a) * cos(m*pi_*y/b);
return u;
}
Vector<Complex> nug_mode_Neumann(const Point&P,Real n,Real m,Parameters& pa=defaultParameters)
{
Vector<Complex> ru = mode_Neumann(P,n,m,pa);
Complex t=ru(1); ru(1)=ru(2); ru(2)=-t;
return ru;
}
Vector<Complex> u_exa(const Point&P,Parameters& pa=defaultParameters)
{ return mode_Neumann(P,1,0,pa); }
Vector<Complex> nug_u_exa(const Point&P,Parameters& pa=defaultParameters)
{ return nug_mode_Neumann(P,1,0,pa); }
// PML matrices
xlifepp::Matrix<Complex> A_alpha(const Point&P,Parameters& pa=defaultParameters)
{
Complex alpha = pa("alpha");
xlifepp::Matrix<Complex> A(3,3);
A(1,1)=1./alpha; A(2,2)=1./alpha; A(3,3)=alpha;
return A;
}
xlifepp::Matrix<Complex> A_alpha_inv(const Point&P,Parameters& pa=defaultParameters)
{
Complex alpha = pa("alpha");
xlifepp::Matrix<Complex> A(3,3);
A(1,1)=alpha; A(2,2)=alpha; A(3,3)=1./alpha;
return A;
}
// null function
Vector<Real> f0 (const Point&P,Parameters& pa=defaultParameters )
{ return Vector<Real>(3);}
//------ main programm -----------
int main(int argc, char** argv)
{
init(argc, argv, _lang=en);
// Geometric data
Real a=1, b=1, w=sqrt(1.25)*pi_; // section lengths
Real h=3., hp=2.; // waveguide length and PML length
Real dx=2./10.; // mesh step
Complex alpha=exp(- i_*pi_/4); // PML coefficient
// mesh waveguide using gmsh
Cuboid C_a(_xmin=0.,_xmax=a,_ymin=0.,_ymax=b,_zmin=-h,_zmax=0.,_hsteps=dx,_domain_name="Omega_g",
_side_names=Strings("Sigma_g","Sigma_0","Gamma","Gamma","Gamma","Gamma")),
C_b(_xmin=0.,_xmax=a,_ymin=0.,_ymax=b,_zmin=0,_zmax=hp,_hsteps=dx,_domain_name="Omega_d",
_side_names=Strings("Sigma_0","Sigma_d","Gamma","Gamma","Gamma","Gamma"));
Mesh mail3d(C_a+C_b, _shape=tetrahedron, _generator=gmsh);
Domain Omega_g=mail3d.domain("Omega_g"), Omega_d=mail3d.domain("Omega_d"),
Sigma_0=mail3d.domain("Sigma_0"), Sigma_g=mail3d.domain("Sigma_g"),
Gamma =mail3d.domain("Gamma");
Sigma_g.setNormalOrientation (_outwardsDomain,Omega_g);
Sigma_0.updateParentOfSideElements();
Parameters pars;
pars<<Parameter(a,"a")<<Parameter(b,"b")<<Parameter(w,"w")<<Parameter(alpha,"alpha");
// Construct Nedelec Spaces (order 1 : NE11 or 2 : NE12)
Space Vg(_domain=Omega_g,_interpolation=NE1_1,_name="Hrot_Ned_g",_optimizeNumbering);
Unknown ug(Vg, _name="ug");TestFunction vg(ug, _name="vg");
Space Vd(_domain=Omega_d,_interpolation=NE1_1,_name="Hrot_Ned_d",_optimizeNumbering);
Unknown ud(Vd, _name="ud"); TestFunction vd(ud, _name="vd");
// Function data
Function uex(u_exa,pars),nuguex(nug_u_exa,pars),fzero(f0,pars);
Function fA(A_alpha,pars),fAinv(A_alpha_inv,pars);
nuguex.require(_n);
// Build system and solve it
BilinearForm auv = intg(Omega_g,rot(ug)|rot(vg)) - w*w*intg(Omega_g,ug|vg )
+ intg(Omega_d,fAinv*rot(ud)|rot(vd)) - w*w*intg(Omega_d,fA*ud|vd );
LinearForm bv = intg(Omega_g,fzero|vg) + intg(Omega_d,fzero|vd);
EssentialConditions ecs = (ncross(ug)|Gamma=0)&(ncross(ud)|Gamma=0)&(ncross(ug)|Sigma_g=nuguex)
& (ncross(ud)-ncross(ug)|Sigma_0=0);
TermMatrix A(auv, ecs, _name="A");
TermVector B(bv, _name="B");
TermVector U = directSolve(A,B);
//Project solution on Lagrange spaces P1 (or P2 if NE12 used) and export solution
Space Wg(_domain=Omega_g,_interpolation=P1,_name="Wg");
Unknown upg(Wg, _name="upg", _dim=3); TestFunction vpg(upg, _name="vpg");
Space Wd(_domain=Omega_d,_interpolation=P1,_name="Wd");
Unknown upd(Wd, _name="upd", _dim=3); TestFunction vpd(upd, _name="vpd");
TermVector Ug = projection(U(ug),Wg,3), Ud = projection(U(ud),Wd,3);
TermVector Up = Ug + Ud; Up.name("Up");
TermVector Uexag(upg,Omega_g,uex), Uexad(upd,Omega_d,uex);
TermVector Uexa = Uexag + Uexad; Uexa.name("Uexa");
saveToFile("solMaxwellPML.vtu",Uexa,Up);
//Compute L2 error on Omega_g (ug) in Nedelec space
TermMatrix M(intg(Omega_g, ug|vg ), _name="M");
TermVector Urot = projection(Uexag,Vg,1) ; //projection on Nedelec space
TermVector E1 = Urot - U(ug);
Real er=sqrt(abs((M*E1|E1))), norm=sqrt(abs((M*Urot|Urot)));
theCout << "L2 error (projection) = " << er << eol;
theCout << "relative L2 error (projection) : " << 100*er/norm << "% \n" << eol;
return 0;
}
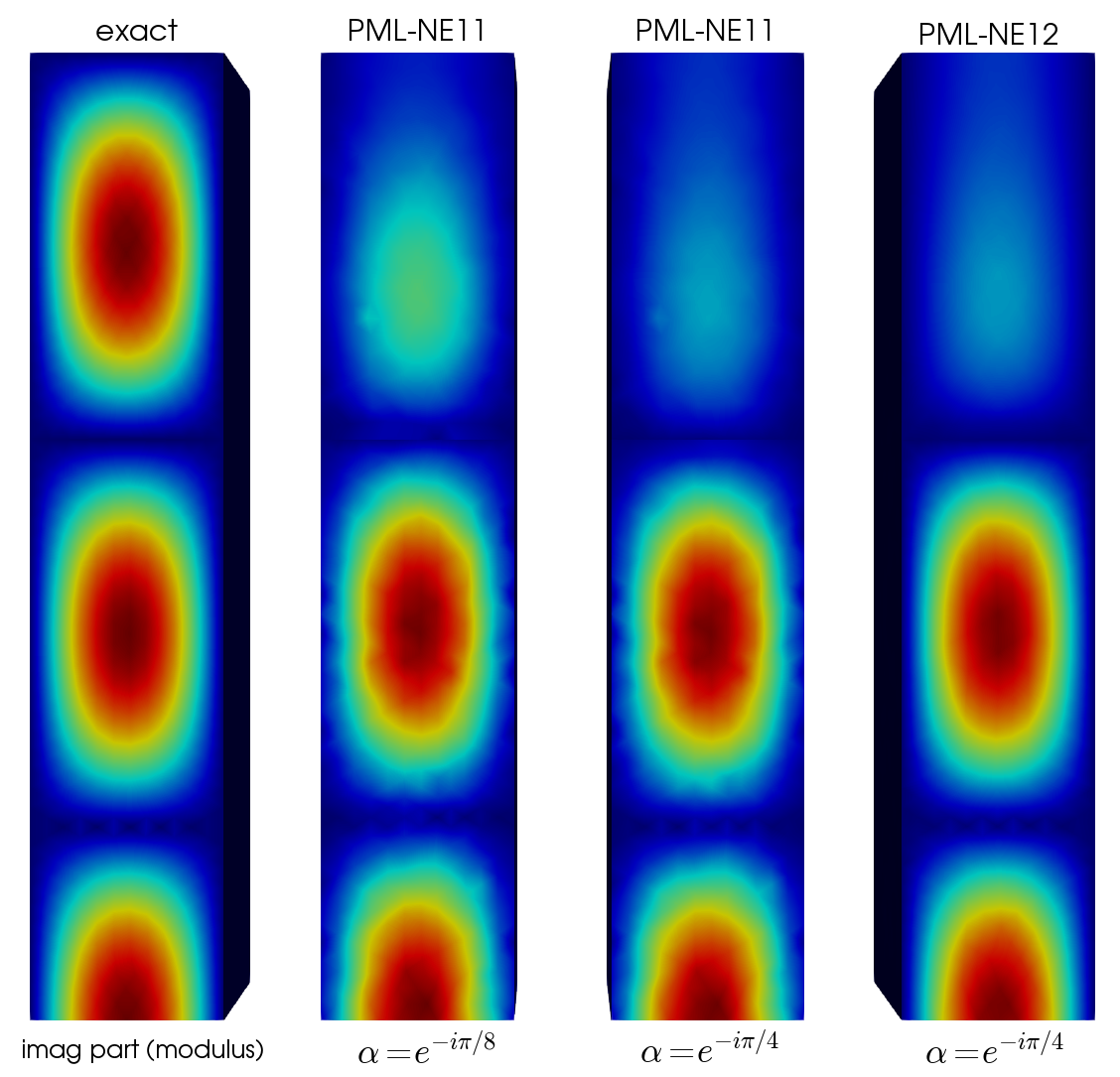
Fig. 13 Examples of solution of Maxwell equation in a half wave-guide using PML and Nedelec first family approximations#