Fictitious domain method

Keywords: PDE:Laplace Method:FEM Method:Mixte FE:Lagrange Solver:Direct

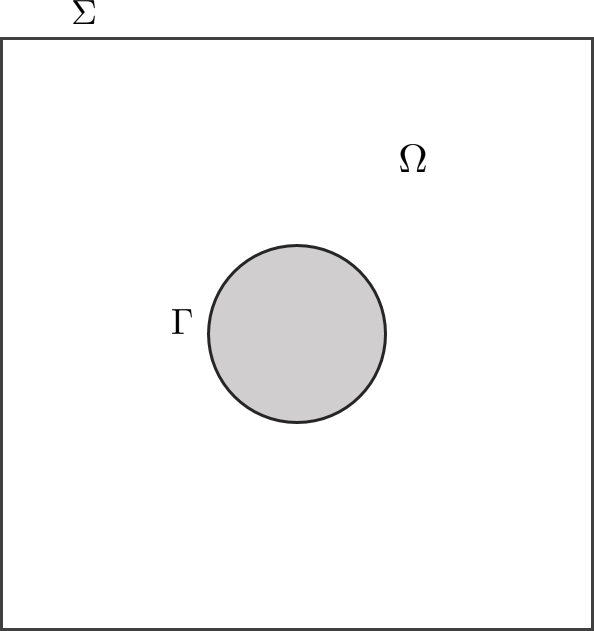
A well-known method to avoid some complex meshes consists in using the fictitious domain method where the boundary condition on an inside obstacle is taken into account by a Lagrange multiplier. To illustrate it, we consider the following 2D Laplace problem in the domain \(\Omega=C\backslash B(O,R)\) with \(C=]0,1[\times]0,1[\) the unit square, \(B(O,R)\) the ball with center \(C\) and radius \(R\) such that \(B\subset C\):

\[\begin{split}\begin{cases} -\Delta u = f & \mathrm{\;in\;}\Omega \\ u=0 & \mathrm{\;on\;}\partial C=\Sigma\\ u=g & \mathrm{\;on\;}\partial B=\Gamma \end{cases}\end{split}\]

Let us introduce the minimization problem:

\[\underset{\tilde{v}\in\tilde{V}(g)}\min \dfrac{1}{2}\int_C |\nabla \tilde{V}|^2-\int_C\tilde{f}\tilde{v}\]

where

\[\begin{split}\tilde{V}(g)=\left\{\tilde{v}\in H^1(C),\ \tilde{v}_{|\Sigma}=0 \mathrm{\;and\;}\tilde{v}_{|\Gamma}=g\right\}\mathrm{\;and\;}\tilde{f}=\begin{cases} f & \mathrm{\;in\;}\Omega \\ 0 & \mathrm{\;in\;}B \end{cases}.\end{split}\]

It has a unique solution \(\tilde{u}\in \tilde{V}(g)\) such that \(\tilde{u}=u\) on \(\Omega\) and there exists \(p\in H^{- \frac{1}{2}}(\Gamma)\) such that

\[\begin{split}\begin{cases} \displaystyle \int_C \nabla\tilde{u}.\nabla \tilde{v}-\int_\Gamma p\,\tilde{v}=\int_C\tilde{f}\, \tilde{v}& \forall \tilde{v}\in H^1_0(C) \\ \displaystyle \int_\Gamma\tilde{u}\, q=\int_\Gamma g\, q &\forall q\in H^{-\frac{1}{2}}(\Gamma), \end{cases}\end{split}\]

where the integrals on \(\Gamma\) are to be understood as the duality product on \(H^{-\frac{1}{2}}(\Gamma)\times H^{\frac{1}{2}}(\Gamma)\).

The key idea of fictitious domain method is to use two different meshes for \(C\) and \(\Gamma\). As a consequence, the computation of integrals on \(\Gamma\) involves shape functions that lie on two different meshes, inducing interpolation operations from one mesh to the other one. XLiFE++ manages this interpolation operations in a hidden way for the user:

#include "xlife++.h"
using namespace xlifepp;

Real R;

Real f(const Point& P, Parameters& pa = defaultParameters)
{if(norm(P)<=R) return 0.;
 return 2*pi_*pi_*sin(pi_*P(1))*sin(pi_*P(2));}
Real g(const Point& P, Parameters& pa = defaultParameters)
{return sin(pi_*P(1))*sin(pi_*P(2));}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp
  
  // create meshes (rectangle and circle)
  R=0.2;
  SquareGeo sq(_xmin =0, _xmax = 1, _ymin = 0, _ymax = 1, _hsteps=0.05, _domain_name = "Omega", _side_names="Sigma");
  Disk circle(_center=Point(0.5, 0.5), _radius =R, _hsteps=0.05, _domain_name = "Gamma");
  Mesh meshS(sq, _shape=triangle);
  Mesh meshG(circle, _shape=segment, _generator=gmsh);
  Domain omega  = meshS.domain("Omega"), sigmat = meshS.domain("Sigma"), gammat = meshG.domain("Gamma");
  
  // create spaces and unknowns
  Space Vt(_domain=omega, _interpolation=P1, _name="Vt");
  Unknown ut(Vt, _name="ut"); TestFunction vt(ut, _name="vt");
  Space W(_domain=gammat, _interpolation=P0, _name="W");
  Unknown p(W, _name="p"); TestFunction q(p, _name="q");
  
  // create bilinear forms and Terms
  BilinearForm at = intg(omega, grad(ut)|grad(vt))-intg(gammat, p*vt) - intg(gammat, ut*q);
  BoundaryConditions bcst = (ut|sigmat =0);
  TermMatrix At(at, bcst, _name="At");
  TermVector Ft(intg(omega, f*vt)-intg(gammat, g*q), _name="Ft");
  
  // solve linear system and save the solution to a vtu file
  TermVector Ut = directSolve(At, Ft);
  saveToFile("Ut", Ut, _format=vtu);
  
  return 0;
}

To extract the solution on the real domain \(\Omega\), a L2 projection is used:

// create a mesh for Omega
Disk disk(_center=Point(0.5,0.5),_radius =R, _hsteps=0.05, _domain_name = "Obstacle", _side_names="Gamma");
Mesh mesh(rectangle-disk);
Domain omega = mesh.domain("Omega");
Space V(omega,P1,"V"); Unknown u(V,"u"); TestFunction v(u,"v");

//compute L2 projection of ut on omega
TermMatrix M(intg(omega,u*v)), M2(intg(omega,ut*v));
TermVector PUt = directSolve(M,M2*Ut);
saveToFile("PUt",PUt,_vtu);

Note that the computation of the matrix M2 also requires a computation of an integral involving two meshes!

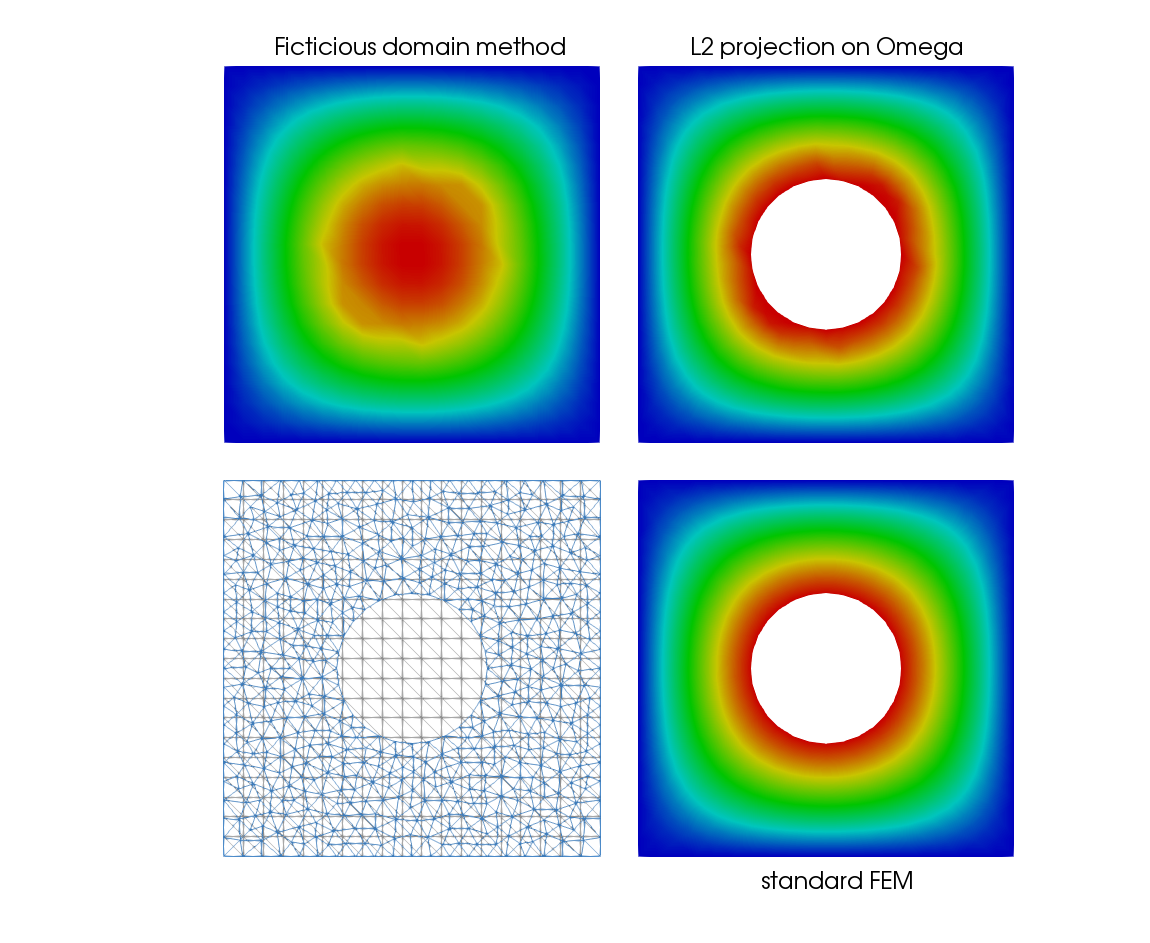
Fig. 27 Solution of the Laplace 2D problem with the fictitious domain method