2D Laplace problem with average condition#

Keywords: PDE:Laplace Method:FEM FE:Lagrange Condition:Average Solver:Direct

As a last example of essential condition, we consider average condition, for instance:

\[\int_\Sigma u=0.\]

Such condition is tricky to take into account in FE softwares. Generally, they do not! Because XLiFE++ uses a powerful process to deal with essential conditions, such condition can be easily addressed:

#include "xlife++.h"
using namespace xlifepp;

Real f(const Point& P, Parameters& pa = defaultParameters)
{return -8.;}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp

  // create a mesh and Domains
  SquareGeo sq(_origin=Point(0., 0.), _length=1, _nnodes=10, _domain_name="Omega", _side_names=Strings("y=0", "x=1", "y=1", "x=0"));
  Mesh mesh2d(sq, _shape=triangle, _generator=structured);
  Domain omega=mesh2d.domain("Omega");
  Domain sigmaM=mesh2d.domain("x=0"), sigmaP=mesh2d.domain("x=1");

  // create interpolation
  Space V(_domain=omega, _interpolation=P2, _name"V");
  Unknown u(V, _name="u");
  TestFunction v(u, _name="v");

  // create bilinear form and linear form
  BilinearForm auv=intg(omega, grad(u)|grad(v));
  LinearForm fv=intg(omega, f*v);
  EssentialConditions ecs= (intg(sigmaM, u) = 0);
  TermMatrix A(auv, ecs, _name="A");
  TermVector F(fv, _name="B");

  // solve linear system AX=F using LU factorization
  TermVector U=directSolve(A, F);
  saveToFile("U_LA", U, _format=vtu);
  return 0;
}

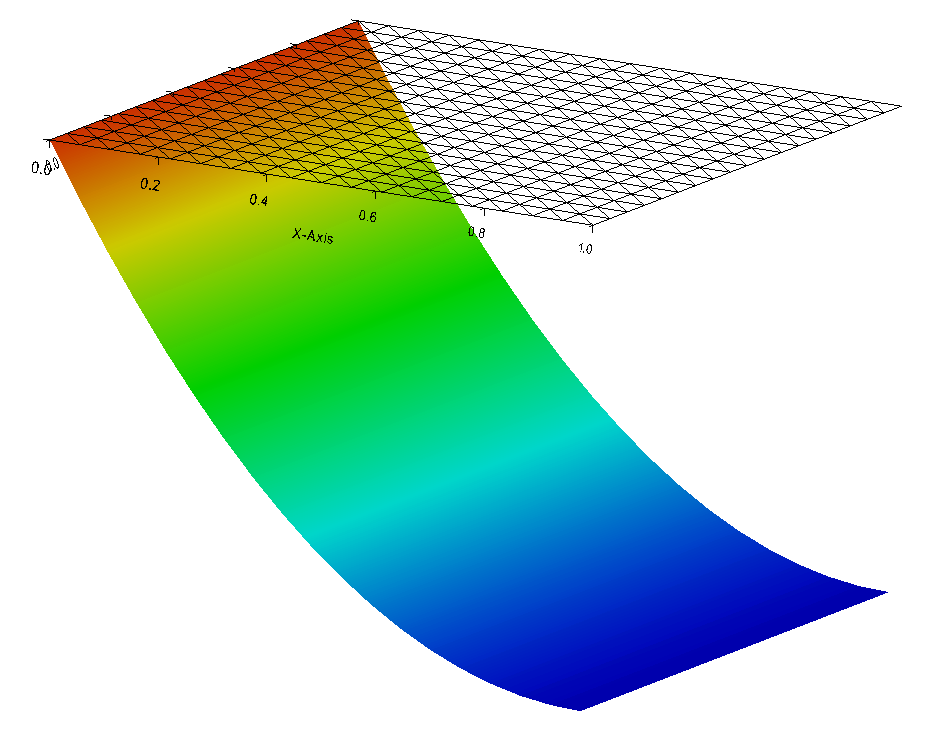
../_images/ex_2d_average.png — Fig. 2 Solution of the Laplace 2D problem with average condition on the unit square \([0,1]^2\)#

Warning

Beware of some average conditions. For instance, when adding the “full” average condition \(\int_{\Omega} u=0\) the resulting reduced matrix is a full matrix. So, the problem is bigger and slower to solve!