1D Laplace problem with Dirichlet condition#

Keywords: PDE:Laplace Method:FEM FE:Lagrange Condition:Dirichlet Solver:Direct

As a first example, we show how to solve the very simple problem, involving Dirichlet conditions:

\[\begin{split}\begin{cases} \displaystyle -u'' = f & \mathrm{\;in\;} \Omega=\left]0,1\right[ \\ u(0)=u(1) =0 & \end{cases}\end{split}\]

Its variational formulation is

\[\begin{split}\left| \begin{array}{c} \mathrm{Find\;}u\in V=\left\{v\in L^2(\Omega),\ v'\in L^2(\Omega),\ u(0)=u(1)=0 \right\} \mathrm{\;such\;that}\\ \displaystyle \int_0^1u'(x)\,v'(x)dx=\int_0^1f(x)\,v(x)dx\ \ \ \forall v\in V. \end{array} \right.\end{split}\]

The following main program corresponds to solving this problem with \(f(x)=1\) using P1 Lagrange element (100 elements):

#include "xlife++.h"
using namespace xlifepp;

Real f(const Point& P, Parameters& pa = defaultParameters)
{return -1.;}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp

  // mesh and domains
  Strings sn("x=0", "x=1");
  Segment seg(_xmin=0, _xmax=1, _nnodes=101, _domain_name="Omega", _side_names=sn);
  Mesh mesh1d(seg, _generator=structured, _name="P1-mesh");
  Domain omega = mesh1d.domain("Omega");
  Domain sigmaL = mesh1d.domain("x=0"), sigmaR = mesh1d.domain("x=1");

  // space, unknows, and test functions
  Space Vh(_domain=omega, _interpolation=P1, _name="Vh");
  Unknown u(Vh, _name="u");
  TestFunction v(u, _name="v");

  // define problem
  BilinearForm a = intg(omega, grad(u)|grad(v));
  LinearForm lf = intg(omega, f*v);
  EssentialConditions ecs = (u|sigmaL = 0) & (u|sigmaR = 0);

  // compute matrix and rhs
  TermMatrix A(a, ecs, _name="A");
  TermVector F(lf, _name="F");

  // solve linear system and save solution
  TermVector U=directSolve(A, F);
  saveToFile("U_1d", U, _format=vtu);
  return 0;
}

The following figure shows a graphical representation of the solution using Paraview:

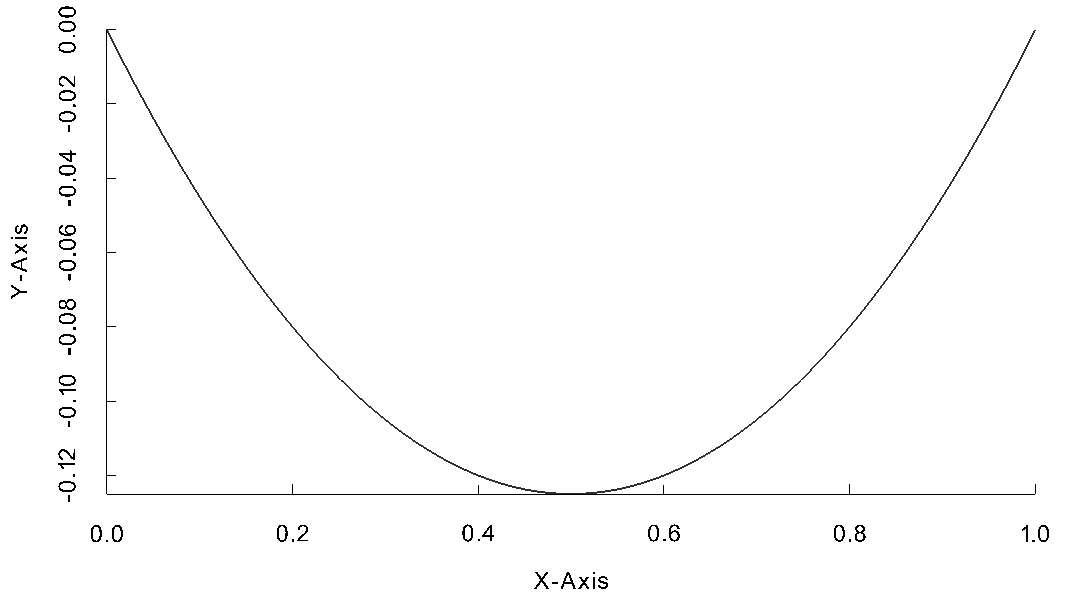
../_images/ex_1d.png — Fig. 3 Solution of the Laplace 1D problem on the unit segment \([0,1]\)#