2D Laplace problem with periodic condition

Keywords: PDE:Laplace Method:FEM FE:Lagrange Condition:Periodic Solver:Direct Solver:Eigen

Now we consider the Laplace problem on the unit square \(\Omega=]0,1[\times ]0,1[\) equipped with Dirichlet condition on and periodic condition:

\[\begin{split}\begin{cases} -\Delta u = f & \mathrm{\;in\;}\Omega \\ u_{|\Gamma^-}=0 \mathrm{\;and\;} u_{|\Gamma^+}=0 & \\ u_{|\Sigma^-}=u_{|\Sigma^+} \mathrm{\;and\;} \partial_xu_{|\Sigma^-}=\partial_xu_{|\Sigma^+} & \end{cases}\end{split}\]

and its variational formulation in \(V=\{v\in H^1(\Omega),\ u_{|\Gamma}=0 \mathrm{\;and\;} u_{|\Sigma^-}=u_{|\Sigma^+}\}\):

\[\begin{split}\left|\begin{array}{c} \mathrm{find\;}u\in V \mathrm{\;such\;that\;} \\ \displaystyle \int_\Omega \nabla u.\nabla v=\int_\Omega f\,v \quad \forall v\in V. \end{array} \right.\end{split}\]

Its approximation by \(P^2\) Lagrange finite element is implemented in XLiFE++ as follows:

#include "xlife++.h"
using namespace xlifepp;

Real f(const Point& P, Parameters& pa = defaultParameters)
{
  Real x=P(1), y=P(2);
  return (4*pi_*pi_*y*(y-1)-2)*sin(2*pi_*x);
}

Vector<Real> mapPM(const Point& P, Parameters& pa = defaultParameters)
{
   Vector<Real> Q(P);
   Q(1)-=1;
   return Q;
}

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp

  // mesh square
  Strings sn("y=0", "x=1", "y=1", "x=0");
  SquareGeo sq(_origin=Point(0., 0.), _length=1, _nnodes=20, _domain_name="Omega", _side_names=sn);
  Mesh mesh2d(sq, _shape=triangle, _generator=structured);
  Domain omega=mesh2d.domain("Omega");
  Domain sigmaM=mesh2d.domain("x=0"), sigmaP=mesh2d.domain("x=1");
  Domain gammaM=mesh2d.domain("y=0"), gammaP=mesh2d.domain("y=1");
  defineMap(sigmaP, sigmaM, mapPM);  // useful to periodic condition

  // create P2 Lagrange interpolation
  Space V(_domain=omega, _interpolation=P2, _name="V");
  Unknown u(V, _name="u");
  TestFunction v(u, _name="v");

  // create bilinear form and linear form
  BilinearForm auv=intg(omega, grad(u)|grad(v));
  LinearForm fv=intg(omega, f*v);
  EssentialConditions ecs = (u|gammaM = 0) & (u|gammaP = 0)
                          & ((u|sigmaP) - (u|sigmaM) = 0); // EssentialConditions ecs
  TermMatrix A(auv, ecs, _name="A");
  TermVector B(fv, _name="B");

  // solve linear system AX=F using factorization
  TermVector U=directSolve(A, B);
  saveToFile("U_LP", U, _format=vtu);

  // Solving eigen problem intg(omega, grad(u)|grad(v))=lambda intg(omega, u*v) with ecs
  BilinearForm uv=intg(omega, u*v);
  TermMatrix Ae(auv, ecs, _reduction=ReductionMethod(_pseudoReduction, 0., 1000.), _name="Ae");
  TermMatrix Me(uv, ecs, _reduction=ReductionMethod(_pseudoReduction, 0., 1.), _name="Me");
  EigenElements eigs=eigenSolve(Ae, Me, _nev=10, _which="SM");
  Complex l1=eigs.value(1);          // first eigen value
  TermVector e1=eigs.vector(1);      // first eigen vector, "eliminated" components are not up to date
  e1.applyEssentialConditions(ecs);  // update "eliminated" components of e1
  eigs.applyEssentialConditions(ecs);// update "eliminated" components of all eigen vectors

  return 0;
}

Note that at corners, periodic condition and Dirichlet condition are redundant. When executing, the following warning message is thrown

Constraints::reduceConstraints() : in essential conditions
    Dirichlet condition u = 0 on y=0
    Dirichlet condition u = 0 on y=1
    periodic condition u|x=1 - u|x=0 = 0
2 redundant constraint row(s) detected and eliminated

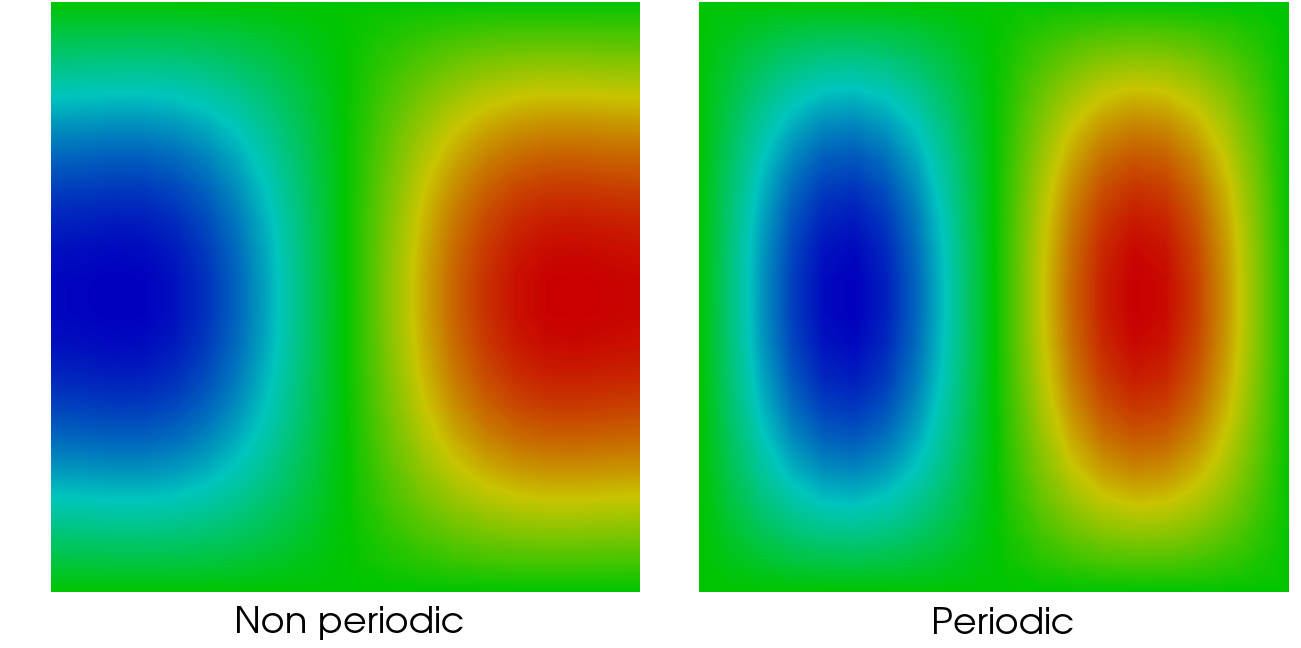
Fig. 14 Solution of the Laplace 2D problem with periodic condition on the unit square \([0,1]^2\)