Eigenvalues and eigenvectors of Laplace operator

Keywords: PDE:Laplace Method:FEM FE:Lagrange Solver:Eigen

This example shows how to get eigen functions of Laplace operator equipped with homogeneous Neumann condition:

\[\begin{split}\begin{cases} -\Delta u + u= \lambda u & \mathrm{\;in\;}\Omega \\ \partial_nu=0 & \mathrm{\;on\;} \partial \Omega \end{cases}\end{split}\]

and its variational formulation in \(V=H^1(\Omega)\):

\[\begin{split}\left|\begin{array}{c} \mathrm{find\;}(u,\lambda)\in V\times \mathbb{R} \mathrm{\;such\;that\;} \\ \displaystyle \int_\Omega \nabla u.\nabla v + \int_\Omega u\, v =\lambda \int_\Omega u\,v \quad \forall v\in V. \end{array} \right.\end{split}\]

#include "xlife++.h"
using namespace xlifepp;

int main(int argc, char** argv)
{
  init(argc, argv, _lang=en); // mandatory initialization of xlifepp

  // mesh square
  SquareGeo sq(_origin=Point(0., 0.), _length=1, _nnodes=20);
  Mesh mesh2d(sq, _shape=triangle, _generator=gmsh);
  Domain omega = mesh2d.domain("Omega");

  // build  P2 interpolation
  Space Vk(_domain=omega, _interpolation=P2, _name="Vk");
  Unknown u(Vk, _name="u");
  TestFunction v(u, _name="v");

  // build eigen system
  BilinearForm auv = intg(omega, grad(u) | grad(v)) + intg(omega, u * v) , 
               muv = intg(omega, u * v);
  TermMatrix A(auv, _name="auv"), M(muv, _name="muv");

  // compute the 10 first smallest in magnitude
  EigenElements eigs = eigenInternSolve(A, M, _nev=10, _mode=krylovSchur, _which="SM");   // internal solver
  theCout << eigs.values;
  saveToFile("eigs", eigs.vectors, _format=vtu);
  return 0;
}

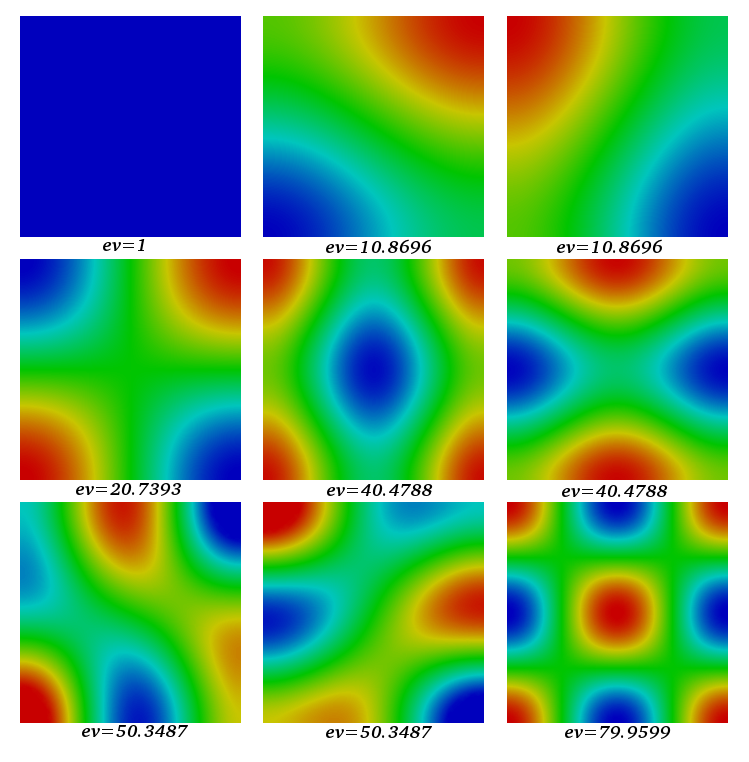
Fig. 22 9 first eigen vectors of the Laplace 2D problem with P2 elements